5.5.2. Обтекание твердых тел

Под обтеканием понимается движение твердых тел относительно жидкой или газовой среды. При этом возникает сила сопротивления R, приложенная к телу и направленная в сторону, противоположную его движению относительно среды, которую можно выразить по аналогии с потерянным давлением с использованием коэффициента гидравлического сопротивления :

, (5.199)

где S - площадь проекции тела на плоскость, перпендикулярную скорости относительного движения, W_ - скорость движения среды относительно тела на бесконечном удалении от него. Сила сопротивления R складывается из двух составляющих - сопротивления трения и сопротивления давления (формы). Первая из этих составляющих обусловлена силами вязкого трения, а вторая - разностью силы давления среды на переднюю (лобовую) и заднюю (кормовую) части тела:

, или . (5.200)

При плавном ламинарном обтекании тела (“ползущее течение”) R_тр > R_g (рис. 5.16а). Такое течение соответствует малым значениям критерия Re (например, для шара при может быть получено теоретическое решение, позволяющее найти силу сопротивления (закон Стокса), из которого следуетR_тр/R_g=2). При увеличении значения Re происходит отрыв гидродинамического пограничного слоя от поверхности тела, вызванный обратным потоком среды за счет положительного градиента давления. За кормовой частью тела образуются завихрения потока (рис. 5.16б). Возрастает доля сопротивления давления и при Re_d > 10³ для шара он становится преобладающим, что приводит к автомодельности коэффициента сопротивления по критерию Рейнольдса.

При достижении Re_d = 2*10⁵ пограничный слой турбулизируется, зона отрыва смещается в кормовую часть шара, что приводит к уменьшению доли сопротивления давления и резкому падению коэффициента сопротивления (так называемый “кризис сопротивления”). Аналогичная картина наблюдается и при поперечном обтекании цилиндра.

Рис.5.16. Обтекание потоком твёрдого тела:

a - ползущее течение; б - отрыв гидродинами­ческого пограничного слоя

Коэффициент сопротивления для сферических частиц в области существования ламинарного пограничного слоя может быть найден из следующих эмпирических соотношений:

Re_d  2 - (в области 0.1 < Re_d < 2 закона Стокса (5.201) действует приближенно)

(5.201)

2 < Re_d  500

(5.202)

500 < Re_d < 2 10⁵ - (автомодельный режим относительно Re) или область квадратичного сопротивления:

 = 0,44 . (5.203)

Для тел, форма которых отличается от сферы, при расчете в качестве определяющего размера принимают диаметр эквивалентного шара, т.е. шара того же объема, что и рассматриваемое тело. В расчет вводится так называемый фактор формы Ф, определяемый как отношение поверхности эквивалентного шара к поверхности тела. Зависимость = f(Re,Ф) находится экспериментально. В справочной литературе имеются соответствующие данные.

Осаждение частиц под действием силы тяжести. Рассмотрим движение частицы в неподвижной среде с меньшей плотностью. В этом случае различают три стадии движения:

1) начальный момент падения тела (переход тела от неподвижного состояния в состояние движения);

2) падение тела с увеличением скорости;

3) падение тела с постоянной скоростью.

Увеличение скорости движения тела от W = 0 до W = const происходит за весьма короткий промежуток времени, в течение которого сила сопротивления среды, пропорциональная скорости, возрастает и уравновешивает вес тела, являющийся равнодействующей сил тяжести и Архимеда. Поэтому для технических расчетов представляет интерес движения тела с постоянной скоростью. Скорость такого равномерного движения частицы в среде называется скоростью свободного осаждения W_ос. Примем, что частица имеет форму шара с диаметром d. При движении частицы с постоянной скоростью на нее действуют следующие силы:

Вес тела:

. (5.204)

Сила сопротивления среды:

, (5.205)

где _ и _ - плотность тела и среды, соответственно.

Уравнение равновесия сил запишется в виде

A = R, или , (5.206)

откуда скорость осаждения будет:

. (5.207)

Значения коэффициентов сопротивления можно определить по зависимостям (5.201)-(5.203), однако какой из них воспользоваться, заранее неизвестно, так как для нахождения Re_d необходимо знать W_ос. Метод последовательных приближений для решения этой задачи довольно трудоемкий.

В.П. Лященко предложил другой метод для определения W_ос. Из формулы (5.207) можно получить

, (5.208)

подставляя в это выражение вместо W_ос ее значение из числа Рейнольдса

, имеем , (5.209)

, (5.210)

где Ar - критерий Архимеда. Таким образом,

. (5.211)

Подставляя в уравнение (5.211) критические (граничные) значения критерия Re_d и соответствующие коэффициенты сопротивления, можно найти критические значения числа Архимеда для каждой области.

Область Re_d  2:

,

. (5.212)

Существование этой области осаждения соответствует условию Ar36.

Область 2 < Re_d < 500:

,

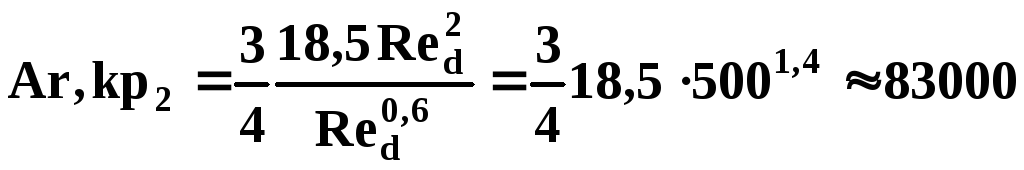(5.213)

Данная область осаждения соответствует изменению критерия Ar в пределах 36 < Ar < 83000. Для автомодельного режима осаждения при Re_d > 500, Ar > 83000. Раccчитав критерий Архимеда (5.210), определив по его значению режим обтекания и выбрав соответствующую зависимость для , по соотношению (5.207) можно найти скорость осаждения, например, приAr < 36 (Re_d < 2)

. (5.214)

Скорость осаждения частиц нешарообразной формы W_ос меньше, чем шарообразных частиц. Ее вычисляют по зависимости

, (5.215)

где  < 1 - коэффициент, зависящий от формы частиц, определяющийся из опыта.