7.2.3. Интегральная форма уравнения массопередачи

Проинтегрировав уравнения (7.82), (7.87) по величине межфазной поверхности всего аппарата или его участка, можно получить уравнения массопередачи в интегральной форме:

. (7.94)

Практический смысл эти уравнения приобретают в случае, если величины коэффициентов массопередачи на рассматриваемом участке интегрирования можно считать постоянными K_y, K_x = const. Тогда их можно вынести из - под интеграла и записать

, (7.95)

, (7.96)

, (7.97)

. (7.98)

Уравнения (7.95) и (7.97) носят название основных уравнений массопередачи. Определим средние движущие силы массопередачи при неизменности расходов по высоте аппарата (G, L=const) для модели идеального вытеснения. Для элементарного участка межфазной поверхности dF количество распределяемого компонента, переносимого из фазы I(y) в фазу II(x) за единицу времени , можно выразить как из уравнения материального баланса (7.68), так и уравнения массопередачи (7.82):

. (7.99)

Разделим переменные и проинтегрируем по поверхности контакта фаз рассматриваемого аппарата (участка аппарата):

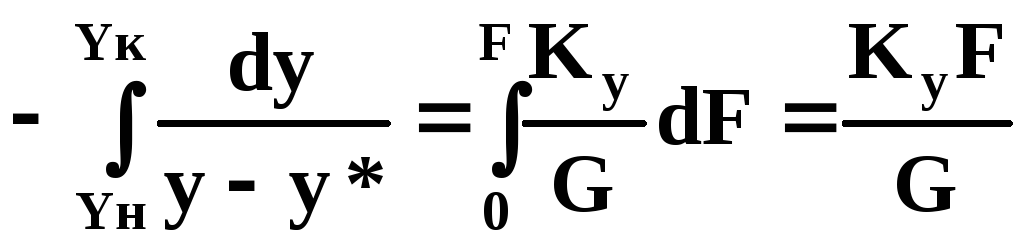. (7.100)

Используя интегральную форму уравнения материального баланса, можно записать

. (7.101)

Найдем из (7.101) G и подставим в (7.100), поменяем пределы интегрирования в левой части этого уравнения, чтобы избавиться от знака «минус», и решим относительно :

. (7.102)

Сопоставив (7.102) и (7.95), найдем :

. (7.103)

Аналогичным образом можно получить выражение и для :

. (7.104)

Расчет средних движущих сил массопередачи предусматривает нахождение определенного интеграла. В частном случае, если в пределах интегрирования коэффициент распределения m = const или линию равновесия можно аппроксимировать прямой, средняя движущая сила определяется средней логарифмической величиной. В этом можно убедиться, подставив соответствующие зависимости в (7.103) или (7.104):

, (7.105)

где y_в и y_н - движущие силы массопередачи в верхнем и нижнем сечениях аппарата (участка аппарата). Аналогичное соотношение справедливо и для x_cp.

Рис. 7.4. Определение средней движущей силы массопередачи при близости равновесной линии к прямой: y_в и y_н - движущие силы массопередачи в верхнем и нижнем сечениях аппарата

Если линия равновесия обладает существенной кривизной, то интегралы в соотношениях (7.103) и (7.104) могут находиться аналитически при условии, что это позволяют зависимости m(x), m(y), либо численными методами на ЭВМ. Возможно и графическое интегрирование. Однако в этом случае, как следует из (7.84), (7.89), K_y , K_x ,по-видимому, нельзя считать постоянными величинами, а следова­тельно, не применимы соотношения (7.95)–(7.104). Один из путей решения проблемы - разбиение аппарата на ряд участков (m), для каждого из которых K_y , K_x можно считать постоянными:

. (7.106)

Для неизменности коэффициентов массопередачи по высоте аппарата необходимо в соответствии с (7.83), (7.84), (7.88), (7.89) выполнение условий: _x, _y, m=const или при постоянных коэффициентах массоотдачи возможность аппроксимации линии равновесия прямой на участке интегрирования, или совокупное изменение этих величин, приводящее к неизменности коэффициентов массопередачи. Последнее маловероятно. В случаях если эти условия не выполняются, K_y, K_x  const либо не соблюдается постоянство расходов фаз по высоте аппарата или структура потока не соответствует модели идеального вытеснения, то для определения поля концентраций по высоте аппарата x(L), y(L), средней движущей силы y_cp, количества вещества, переносимого в аппарате из одной фазы в другую за единицу времени , необходимо решать систему дифференциальных уравнений, аналогичную (4.112)-(4.117).

Структура потока влияет на величину средней движущей силы массопередачи так же, как и на среднюю движущую силу теплоотдачи или теплопередачи. Максимальна движущая сила для МИВ, а минимальна для МИС (см. рис. 4.2).