7.2.2. Уравнение массопередачи в локальной форме

Запишем уравнения массоотдачи для двух фаз I и II, обозначив их индексами y и x соответственно. В качестве движущих сил используем разность концентраций. С целью упрощения записи будем опускать верхний индекс «g»и нижний «y» в обозначении межфазного потока, верхний индекс «я» при обозначении концентраций, нижний индекс «i», соответствующий номеру компонента. Предположим, что распреде­ляемый компонент переходит из фазы I в фазу II:

, (7.78) , (7.79)

где х, y - рабочие концентрации распределяемого компонента в фазах.

Используем допущение, принятое нами в разделе 4.4, об отсутствии сопротивления переносу вещества со стороны межфазной поверхности или равновесии на границе раздела фаз, выразив его в виде

или . (7.80)

Дальнейший вывод уравнения массопередачи аналогичен (4.91) - (4.93). Выразим x^г из (7.80), подставим в (7.79). Разрешим уравнения (7.78) и (7.79) относительно разности концентраций и сложим. Найдем из полученного уравнения выражение для потока:

. (7.81)

Нетрудно видеть, что если коэффициент распределения не зависит от состава фазы, m(x^г) = m(x) = m, то уравнение (7.81) упрощается:

, (7.82) . (7.83)

В общем случае уравнение (7.81) можно привести к традиционному виду уравнения массопередачи (7.82) с использованием (7.78)-(7.80). Однако коэффициент массопередачи K_y при зависимости m от состава будет определяться следующим образом:

, (7.84) 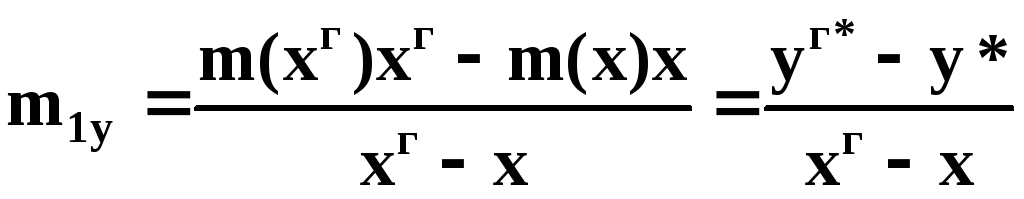. (7.85)

Для нахождения m_1y требуется знать величину граничной концентрации x^г, которая определяется из решения системы уравнений (7.78) - (7.80). Если для сечения аппарата А‑А равновесная линия на участке от x_A до x_A^* может быть аппроксимирована прямой, то для отыскания m_1y нет необходимости решать систему уравнений и определять x_A^г, в этом случае (рис. 7.3)

. (7.86)

Если y^г из (7.80) подставить в (7.78), а затем провести вышеуказанные преобразования, то уравнение массопередачи примет вид

, (7.87)

, (7.88) , (7.89)

. (7.90)

При аппроксимации равновесной линии прямой на участке от y_A^* до y_A величина m_1x = m_1y = m₁ и определяется по соотношению (7.86).

Итак, мы получили уравнения массопередачи, движущими силами которых являются разности рабочей и равновесной концентраций компонента в одной из фаз. Использование коэффициента массопередачи K_y или K_x зависит от выбора фазы, через концентрации в которой записана движущая сила. При расчете и использовании коэффициентов массоотдачи и массопередачи необходимо соблюдать соответствие размерностей потоков, движущих сил, коэффициентов распределения, массоотдачи и массопередачи. Если движущая сила выражена в мольных долях, а поток вещества - в кмоль/(м²с), то коэффициенты массоотдачи и массопередачи будут иметь размерность кмоль/(м²с мольная доля). Коэффициент распределения при этом также должен связывать равновесные концентрации компонента, выраженные в мольных долях. Из уравнений (7.82) и (7.87) легко установить связь между этими коэффициентами:

. (7.91)

Рис. 7.3. Определение величин m₁: ,,

В частных случаях соотношение (7.91) может упрощаться. Так, при m=const оно сводится к соотношению

. (7.92)

При аппроксимации равновесной линии прямой на участке от x до x* из (7.86) следует

. (7.93)

В заключение можно сделать вывод, что в общем случае при существенной зависимости коэффициента распределения от состава использование уравнений массопередачи (7.82) и (7.87) не дает преимуществ по сравнению с (4.94), в котором движущей силой является разница химических потенциалов компонента в фазах. Оба вида уравнений требуют знания зависимости летучестей компонента от состава фаз. Более того, применение уравнений (7.82) или (7.87) предполагает еще и решение системы уравнений (7.78)-(7.80) для нахождения x^г, y^г. Однако для частных случаев постоянства коэффициента распределения или возможности аппроксимации равновесной линии на участке от x до x* прямой более удобны и наглядны уравнения (7.82), (7.87).