7.8. Массоперенос в многокомпонентных системах
Основной особенностью массопереноса в многокомпонентных смесях является зависимость потока каждого компонента i от градиентов концентраций всех компонентов (2.22), что приводит к появлению матрицы коэффициентов многокомпонентной диффузии Di,j, а также матриц коэффициентов массоотдачи i,j и массопередачи Ki,j. Вывод соотношений для последних возможен лишь в матричной форме. Действия с матрицами рассматриваются в приложении П1.5.
7.8.1. Уравнения массоотдачи
По аналогии с выводом уравнений импульсо- и теплоотдачи, а также массоотдачи в бинарных смесях, проведенном в разделе 4.1, получим уравнение массоотдачи для многокомпонентных систем. Все уравнения будут записываться в матричной форме. В соответствии с (1.31) поток вещества компонента i в направлении, перпендикулярном границе раздела фаз за счет молекулярного и турбулентного механизмов переноса, может быть представлен в виде
,
(7.229)
,
(7.230)
или
, (7.231)
где [ гDi,j ] - квадратная матрица размерностью (n-1)(n-1); [ гjgi,y ], [ci] - матрицы-столбцы размерности (n-1) 1.
Проекцию потока каждого компонента на ось y на расстоянии y от межфазной поверхности гjgi,y(y) можно представить в виде произведения потока через межфазную поверхность и его относительного изменения j*i(y):
или
(7.232)
где [j*i,i] - диагональная матрица.
Подставим (7.232) в (7.231), разделим переменные и проинтегрируем по толщине диффузионного пограничного слоя:
,
(7.233)
,
(7.234)
,
(7.235)
,
(7.236)
,
(7.237)
где
- обратная матрица.
Для частного случая пленочной модели массоотдачи (раздел 7.4) достаточно просто определяется явный вид элементов матрицы коэффициентов массоотдачи:
,
,
(7.238)
.
7.8.2. Уравнения массопередачи
Аналогично тому, как в разделе 7.2.2 получено в локальной форме уравнение массопередачи для бинарных смесей, получим соответствующие уравнения для многокомпонентных систем. Для простоты допустим неизменность коэффициентов распределения mi, а также опустим верхний «g» и нижний «y» индексы в записи потоков:
,
(7.239)
,
(7.240)
.
(7.241)
Выразим xгi из (7.241), подставим в (7.240), разрешим уравнения (7.239), (7.240) относительно разности концентраций и сложим, а затем решим относительно потока:
,
(7.242)
,
(7.243)
,
(7.244)
,
(7.245)
,
(7.246)
,
(7.247)
.
(7.248)
В том
случае если коэффициенты распределения
miзависят
от состава фаз и эта зависимость для
участка аппарата может считаться
линейной, то по аналогии с (7.84)–(7.86) в
уравнении массопередачи (7.248) диагональная
матрица коэффициентов распределения
[mi,i]
заменится на квадратную [
],
элементы которой находятся как
.
Если элементы матрицы коэффициентов массопередачи можно считать неизменными, то справедливо уравнение массопередачи в интегральной форме:
,
(7.249)
.
(7.250)
Даже
при постоянных расходах фаз и линейной
зависимости y*i(xi)
величины
yi,cp
каждого компонента определяются матрицей
коэффициентов массопередачи и движущими
силами по всем компонентам в верхнем и
нижнем сечениях аппарата yi,cp
=
f(Kyi,j
,
,
).
Для отыскания yi,cp
необходимо использовать стандартную
процедуру диагонализации матрицы
коэффициентов массопередачи.
В частном случае, когда концентрации распределяемых компонентов в инертных малы для каждой из фаз, что зачастую наблюдается при абсорбции или экстракции, можно считать смеси бесконечно разбавленными. Для них недиагональные элементы матрицы коэффициентов массопередачи стремятся к нулю и поток каждого распределяемого компонента будет пропорционален лишь собственной средней движущей силе, которая для модели идеального вытеснения при постоянных значениях коэффициентов распределения может быть найдена из выражения
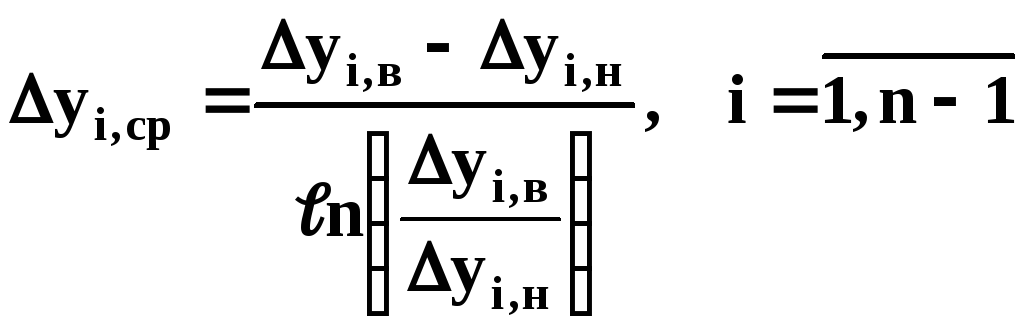. (7.251)
Как и в случае бинарных смесей можно использовать модифицированные уравнения массопередачи:
,
(7.252)
,
(7.253)
, (7.254)
,
(7.255)
,
(7.256)
. (7.257)
Кроме того, можно ввести матрицу чисел единиц переноса
,
(7.258)
,
(7.259)
.
(7.260)
По аналогии с бинарными системами общие высоты и числа единиц переноса выражаются через соответствующие фазовые (частные) величины.