. . . . . . . . . . . . . . . . . . . .

, (7.218)

, (7.219)

. (7.220)

. . . . . . . . . . . . . . . . . . . . .

Расчет заканчивается при значении , для которого начинает выполняться условие , при этом число тарелокN = . Следует отметить, что для аппаратов со ступенчатым контактом фаз рабочая линия приобретает дискретный характер и говорить о связи рабочих концентраций фаз имеет смысл лишь для определенных сечений аппарата, например, непосредственно под каждой тарелкой (7.217), (7.220). Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм имеет смысл реализовать на компьютере.

Для ориентировочных расчетов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.

Определение числа тарелок с помощью кинетической кривой. Упрощение по сравнению с предыдущим способом заключается в следующем: эффективности по Мэрфри рассчитываются не для каждой тарелки, а лишь для нескольких сечений колонны; аналитическое решение уравнений (7.215)-(7.220) заменяется графическим. Алгоритм действий следующий:

а) на X - Y диаграмме строятся рабочая и равновесная линии (рис. 7.10);

б) для нескольких сечений аппарата (нескольких рабочих концентраций x, y, x, y, x,y... рассчитываются эффективности тарелки по Мэрфри E_y, E_y, E_y ...;

в) находятся величины y^k, y^k, y^k ...

, (7.221)

. . . . . . . . . . . . . . . . . . . . . . . .

г) на X - Y диаграмме наносятся точки с координатами x, y^k; x, y^k; x, y^k;... и соединяются линией, называемой кинетической кривой. Если все E_y < 1, то кинетическая кривая располагается между рабочей и равновесной линиями; если все E_y = 1, то кинетическая кривая, как следует из (7.221), совпадает с равновесной линией;

д) из точки А₁ с координатами x₁ = x_k, y₁ = y_н проводится линия, параллельная оси y, до пересечения с кинетической кривой. Находится ордината точки В₁ (x₁, y₂), т.е. графическим способом решается уравнение (7.216). Из точки В₁ проводится прямая, параллельная оси x, до пересечения с рабочей линией; находится абсцисса точки А₂ (x₂, y₂), т.е. графически решается уравнение (7.217);

е) процедура пункта д) повторяется для точки А₂, затем А₃ и т.д. до тех пор, пока для ординаты точки не выполнится условие. На этом построения заканчиваются, необходимое число тарелок в колоннеN = .

Рис. 7.10. Определение числа тарелок с помощью кинетической кривой:

1 - рабочая линия; 2 - равновесная линия; 3 – кинети­ческая кривая

Таким образом, аналитическое решение уравнений (7.215)-(7.220), составляющих алгоритм потарелочного расчета, заменяется графическим вписыванием и определением количества прямоугольных ступеней между рабочей линией и кинетической кривой в заданном интервале изменения рабочих концентраций.

Определение числа тарелок с помощью к.П.Д. Колонны. Вводится понятие к.П.Д. Колонны  как отношение числа теоретических тарелок Nт к числу действительных тарелок n:

. (7.222)

Величина  находится из эмпирических корреляций. Недостатком данного способа является сложность обобщений к.п.д. колонны. Надежные результаты для  могут быть найдены лишь при наличии опытных данных по работе идентичной колонны.

Алгоритм определения необходимого числа тарелок N в колонне следующий:

а) аналитическим или графическим способом находится число теоретических тарелок N_т. Аналитический способ заключается в решении уравнений (7.215)-(7.220) при = 1. Графический способ определения N_т аналогичен рассмотренному выше, однако поскольку все E_y = 1 и кинетическая кривая совпадает с равновесной линией, отпадает необходимость выполнения пунктов б) - г) и прямоугольные ступени вписываются между рабочей и равновесной линиями;

б) по известным эмпирическим формулам рассчитывается к.п.д колонны ;

в) из соотношения (7.222) определяется число действительных тарелок N.

Остановимся теперь более подробно на определении эффективности тарелки по Мэрфри .

Расчет эффективности тарелки по Мэрфри. Введем еще одну величину - локальную эффективность массопередачи -й тарелки , характеризующую в отличие от эффективности по Мэрфри не всю тарелку, а бесконечно малый ее участок. Рассматривается вертикальное прохождение газа сквозь барботажный слой в фиксированной точке на плоскости тарелки.

, (7.223)

где - локальные, а не средние по сечению, как в (7.214), концентрации распределяемого компонента в газовой фазе на входе и выходе из барботажного слоя -й тарелки; - концентрация в газовой фазе, равновесная с концентрацией распределяемого компонента в жидкой фазе для данной точки на поверхности тарелки. Благодаря интенсивному воздействию газового потока предполагается, что жидкость полностью перемешана в вертикальном направлении. Таким образом, на локальную эффективность будет влиять структура потока лишь газовой фазы.

Допустим, что газ движется в барботажном слое в соответствии с моделью идеального вытеснения. Получим в этом случае расчетное соотношение для . Запишем выражение общего числа единиц переноса для выбранного локального участка барботажного слоя на -й тарелке:

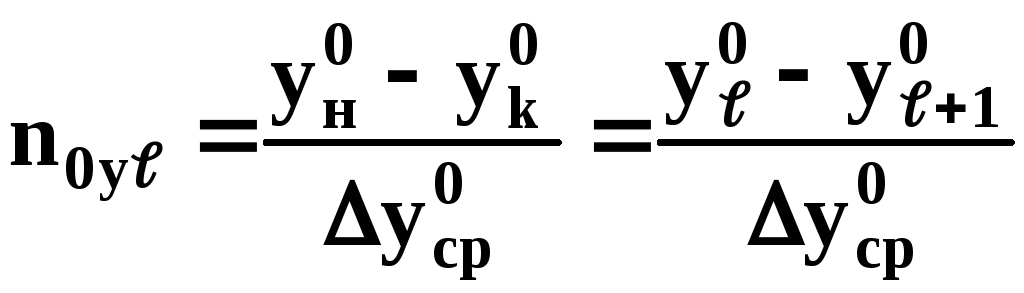. (7.224)

В случае МИВ для газовой фазы и МИС для жидкой (рассматривается вертикальное направление в барботажном слое) величина y⁰_cp будет определяться как средняя логарифмическая (аналогично 5.31):

,

. (7.225)

В знаменателе выражения, стоящего под логарифмом, прибавим и отнимем , а затем числитель и знаменатель разделим на :

(7.226)

Решим последнее уравнение относительно :

. (7.227)

Мы получили соотношение, связывающее локальную эффективность массопередачи при идеальном вытеснении по газу с общим числом единиц переноса на тарелке. В соответствии с (7.121)

, (7.228)

где f - площадь рабочего сечения тарелки; G - расход газовой фазы; - коэффициент массопередачи, отнесенный к единичной площади рабочего сечения тарелки, при расчете которого использованы температура, давление, состав, коэффициент распределения и теплофизические свойства, соответствующие тарелке под номером . Из (7.227) следует, что чем больше коэффициент массопередачи, тем больше и . При   1 при  0  0. Таким образом, локальная эффективность изменяется от 0 до 1.

Можно получить зависимость () для других моделей структуры газового потока, однако качественный характер зависимости при этом не изменится.

Чтобы связать локальную эффективность массопередачи с эффективностью тарелки по Мэрфри, необходимо учесть структуру жидкостного потока на тарелке в горизонтальном направлении. Так, в случае полного перемешивания жидкости на тарелке . Для других моделей структуры жидкостного потока они не совпадают, соответствующие выражения для идеального вытеснения, диффузионной и ячеечной моделей приведены в [28]. Там же приведены соотношения, позволяющие учитывать влияние натаких явлений, уменьшающих эффективность по Мэрфри, как унос капель жидкости газовым потоком и байпас (проскок части жидкости без взаимодействия с газовым потоком). Величина эффективности тарелки по Мэрфри увеличивается при уменьшении обратного перемешивания по жидкости вдоль тарелки, достигая максимума для МИВ. Она в отличие от локальной эффективности может быть больше единицы.

Существенной проблемой при расчете эффективности тарелки по Мэрфри является определение параметров модели структуры жидкостного потока Pe_L (МД) или m - число ячеек (МЯ). Они могут быть найдены из эмпирических корреляций, а в случае отсутствия таковых для тарелок определенной конструкции и размеров получены методы сопряженного физического и математического моделирования. Кроме того, данный метод позволяет непосредственно определять эффективность тарелки по Мэрфри на основе расчета полей концентраций.

Таким образом, можно сформулировать основные этапы проектного технологического расчета аппарата со ступенчатым контактом фаз.

1. Предварительное определение расхода второй фазы L, если эта величина не задана.

2. Предварительное определение скоростей движения фаз и диаметра аппарата D.

3. Предварительное нахождение межтарельчатого расстояния h_м.

4. Определение числа тарелок N с помощью потарелочного расчета, в ходе которого для каждой тарелки находятся коэффициенты массопередачи , числа единиц переноса, локальные эффективности, параметры модели структуры жидкостного потока на тарелкеили, унос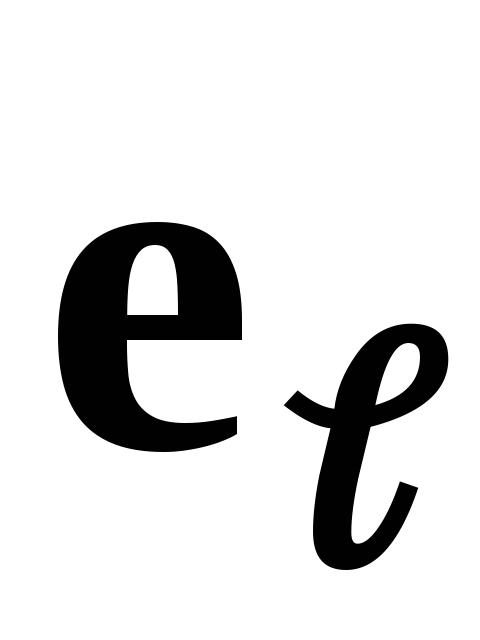, эффективность тарелки по Мэрфри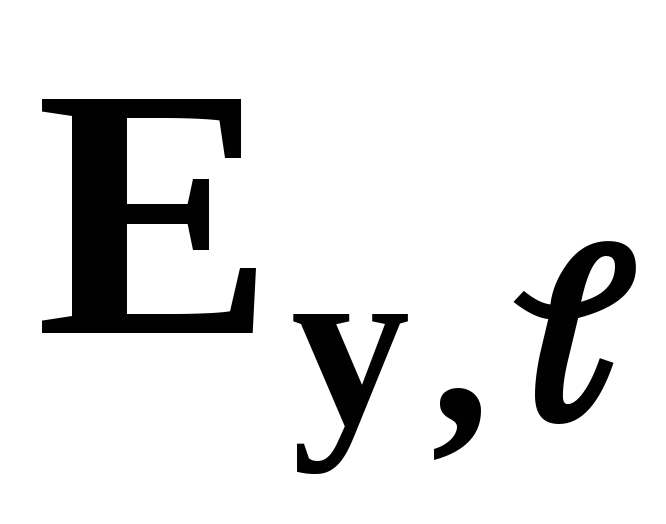. (При ориентировочном расчете с помощью кинетической кривой можно определить все вышеперечисленные величины лишь для нескольких сечений аппарата).

5. Расчет высоты колонны по (7.213).

6. Оптимизация размеров аппарата. В качестве параметров оптимизации могут использоваться расход второй фазы L, скорость газовой фазы W⁰_y или диаметр аппарата D, межтарельчатое расстояние h_м, конструктивные особенности тарелок, например, тип тарелки, диаметр отверстий, высота сливной перегородки и т.д.

Необходимо отметить, что понятие теоретической ступени изменения концентрации (теоретической тарелки) может использоваться и для определения высоты аппарата с непрерывным контактом фаз, которая находится как произведение N_т на h_э - высоту, эквивалентную одной теоретической ступени (ВЭТС). Последняя, как правило, рассчитывается по эмпирическим соотношениям. Недостатком этого способа является изменение h_э по высоте аппарата при наличии кривизны линии равновесия.