7.5. Массообмен с тонкой пленкой жидкости

В промышленных аппаратах часто используется массообмен с тонкой пленкой жидкости, стекающей по твердой поверхности. При этом массопередача может происходить как между пленкой и твердой фазой, так и между пленкой и газовой фазой, контактирующей с внешней поверхностью пленки. На примере массообмена с жидкой пленкой покажем возможность нахождения коэффициентов массоотдачи на основе исчерпывающего описания процессов переноса, а также с использованием упрощенных моделей.

Массоотдача в газовой фазе Рассмотрим массопередачу между газом, движущимся по вертикальной трубе круглого сечения, и жидкой пленкой, стекающей по внутреннему периметру трубы. Возможны

следующие варианты направления движения фаз: нисходящий прямоток (газ и пленка движутся вниз), противоток (газ движется вверх, а пленка вниз), восходящий прямоток (пленка движется вверх, увлекаемая потоком газа). Если ввести среднемассовую концентрацию по аналогии со среднемассовой температурой(6.85), то все соотношения, описывающие массоотдачу в газовой фазе, будут аналогичны соотношениям для теплоотдачи в трубе (раздел 6.2.2). Отличие будет заключаться лишь в том, что диаметр проходного сечения для газа необходимо уменьшить на толщину пленки, а скорость газа рассматривать относительно границы раздела фаз газ – жидкость:

, (7.151) , (7.152)

, (7.153)

где d - внутренний диаметр трубы,  - толщина пленки, - средняя скорость газа относительно границы раздела фаз газ - жидкость,- средняя скорость газа относительно стенок трубы, - скорость движения границы раздела фаз газ - жидкость относительно стенок трубы.

В режиме слабого взаимодействия газа с жидкостью < 3 м/с, при котором поток импульса через границу раздела фаз газ - жидкость значительно меньше потока импульса на границе жидкость - стенка, скорость может определяться из соотношений для гравитационного течения пленки. При сильном взаимодействии для нахождениянеобходимо рассматривать импульсопередачу из газовой в жидкую фазу. На практике для тонких пленок при<<d зачастую пренебрегают отличиями в движении газа, вызванными наличием пленки, используя для расчета массоотдачи соотношения, аналогичные теплоотдаче, без учета (7.151)-(7.153).

Массоотдача в ламинарной безволновой пленке. Пленку будем рассматривать гидродинамически стабилизированную, в режиме слабого взаимодействия с газовым потоком. В этом случае стационарный массообмен в ней описывается уравнением

, (7.154)

где x - вертикальная (продольная) координата, совпадающая с направлением движения пленки, y - поперечная координата. Вследствие малой толщины пленки ( << d) даже при ее течении в круглой трубе задачу можно рассматривать как плоскую в декартовых координатах. Если считать, что является известной функцией отy, а = const, то уравнение (7.154) имеет точное решение и поле концентраций с_i(x,y) представляется в виде бесконечного ряда, содержащего параметры, определяемые из граничных условий. Однако в некоторых случаях можно получить аналитическое решение.

Рассмотрим простейший, с математической точки зрения, случай: на внешней границе пленки распределяемый компонент абсорбируется из газовой фазы, а на внутренней адсорбируется стенкой; все сопротивление массопередачи сосредоточено в жидкой фазе, т.е. на границе с газом с_i=с_i^г=const, а на границе со стенкой с_i=0. В этом случае при стабилизированном массообмене с_i не будет зависеть от координаты x и левая часть уравнения (7.25) обратится в ноль. Совместив начало координаты y с границей раздела газ - жидкость, представим упростившуюся задачу в следующем виде

, (7.155)

; . (7.156)

Этот случай аналогичен теплоотдаче при пленочной конденсации пара на вертикальной стенке с постоянной температурой (раздел 6.23) или теплопроводности через плоскую стенку (6.5), (6.6). Проинтегрировав уравнение (7.155) с граничными условиями (7.156), получим линейный профиль концентрации и, следовательно, по (1.23) постоянный поток вещества j_i,y = const. Все эти условия соответствуют пленочной модели массоотдачи, толщина пограничного слоя при этом совпадает с толщиной пленки и коэффициент массоотдачи _i определяется по (7.133):

или . (7.157)

Это один из немногих случаев, когда пленочная модель адекватно описывает реальный процесс массоотдачи.

Рассмотрим более сложный, но более часто встречающийся на практике случай: абсорбцию из газа жидкой пленкой на участке массообменной стабилизации при условии, что распределяемый компонент не успевает достаточно глубоко проникнуть вглубь пленки. Последнее условие позволяет рассматривать только область y<<, в которой (см. раздел 6.4.1). Совместим начало координаты x с поперечным сечением пленки, в котором возникает контакт газовой фазы с жидкой и начинается процесс абсорбции. Граничные условия с_i(x,y) будут иметь вид

. (7.158)

От пространственной координаты x можно перейти ко времени t:

. (7.159)

С использованием новой переменной уравнение (7.154) приобретет вид (7.142), а граничные условия (7.158) совпадут с (7.143). Следовательно, процесс массоотдачи в данном случае можно описать с помощью модели проницания. Достаточно в решения (7.144)-(7.150) подставить (7.159). Локальный и средний коэффициенты массоотдачи примут вид

, (7.160)

. (7.161)

Условиями применимости данного решения являются малость толщины диффузионного пограничного слоя (7.150) по сравнению с толщиной пленки, а также . Если считать, что эти условия с достаточной точностью выполняются при _g /  < 0,1, то

,

или . (7.162)

Коэффициенты массоотдачи (7.160)-(7.161) можно представить в безразмерном виде при условии (7.162):

, (7.163)

. (7.164)

Напомним, что эти соотношения получены для начального участка массообменной стабилизации. Для описания стабилизированного массообмена в пленке обычно используют по-иному определенные коэффициенты массоотдачи:

, (7.165) , (7.166)

. (7.167)

Средняя движущая сила массоотдачи в (7.167) находится как среднелогарифмическая величина по аналогии с (5.31). На начальном участке при _g /  << 0,1 с_i  c_i⁰, _i  _i. Однако при увеличении Fо_g,б различие между _i и _i может быть весьма существенным. Точное решение уравнения (7.154) с граничными условиями (7.168) может аппроксимироваться следующими зависимостями:

; (7.168)

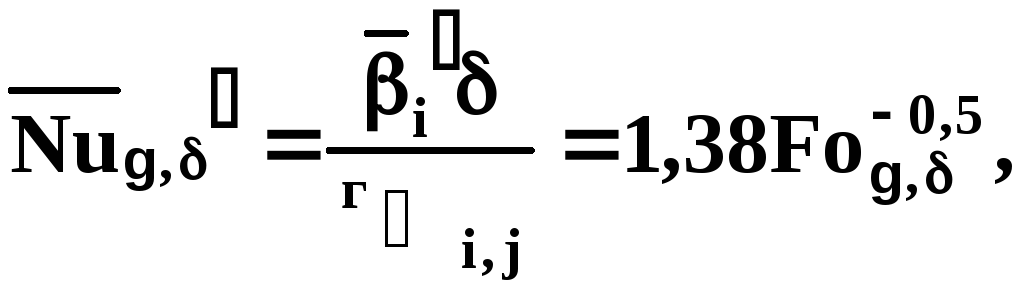
; (7.169)

. (7.170)

В пределе при больших значениях критерия Фурье стабилизированная массоотдача от границы газ-жидкость к ламинарной пленке характеризуется постоянным критерием Нуссельта Nu_g,=3,41.

Последнее соотношение в (7.168) выражает отсутствие переноса компонента i через границу пленки со стенкой. Можно рассмотреть и противоположный случай: распределяемый компонент переходит из твердой фазы в пленку, а границу пленка - газ не пересекает (экстрагирование, растворение стенки). Рассмотрим начальный участок массообменной стабилизации. Ось Y направим от стенки к границе пленки с газом. Тогда задача будет состоять в решении уравнения (7.154) с граничными условиями (7.158). Однако в отличие от рассмотренного выше случая абсорбции нет возможности использовать модель проницания, так как нельзя принять допущения о постоянстве скорости W_x вблизи твердой поверхности. Имея в виду параболический профиль скорости в ламинарной пленке (5.127), более разумно допущение ее линейной зависимости при y << :

. (7.171)

C учетом этого уравнение (7.154) примет вид

. (7.172)

Процедура его решения аналогична изложенной при решении уравнения нестационарной теплопроводности в полубесконечном слое (раздел 6.4). Осуществив переход к новым безразмерным переменным  и , уравнение в частных производных (7.172) трансформируется в обыкновенное:

, (7.173)

, (7.174) , (7.175)

. (7.176)

Учитывая, что

, (7.177)

где Г(z) - табулированная в справочниках гамма - функция, решение может быть представлено в виде

, (7.178)

. (7.179)

Зная поле концентраций (7.178), аналогично (7.146)-(7.150) получим поле диффузионных потоков, локальные и средние коэффициенты массоотдачи, а также толщину диффузионного слоя:

, (7.180)

, (7.181)

, (7.182)

, (7.183)

. (7.184)

Ограничив аналогично (7.162) область применимости данных соотношений условием _g/ < 0,1, его и критериальную форму коэффициентов массоотдачи можно представить в виде

или , (7.185)

, (7.186)

. (7.187)

Использовав коэффициенты массоотдачи _i , определяемые по (7.165), точное решение уравнения (7.154) с параболлическим профилем скорости и граничными условиями (7.168) для массоотдачи от границы стенки в ламинарную пленку может быть аппроксимировано:

(7.188)

(7.189)

Проанализируем наличие аналогии переноса массы и других субстанций в жидкой ламинарной пленке, стекающей по вертикальной стенке под действием силы тяжести. Предполагать гидродинамическую аналогию массообмена в данном случае не следует вследствие отличия уравнений движения (6.126) и конвективной диффузии (7.154). В первом присутствует источник импульса, обусловленный силой тяжести, а во втором таковой отсутствует. Соответственно, в области стабилизиро­ванного импульсо - и массообмена пленки со стенкой Nu_г, = 3  Nu_g, = 1,88 при любых значениях Pr_g. Импульсоотдача от границы с газом к пленке в режиме слабого взаимодействия вообще пренебрежимо мала. Идентичность дифференциальных уравнений переноса тепла и массы в пленке предопределяет возможность аналогии при идентичности граничных условий. Рассмотренный первым случай одновременной абсорбции распределяемого компонента пленкой и его адсорбции стенкой идентичен по граничным условиям пленочной конденсации пара (6.136), (6.137) и Nu_т, = Nu_g, = 1. Результаты, полученные для массоотдачи от границы с газом к пленке, можно применить для теплоотдачи от газовой фазы к пленке при нулевом потоке тепла через стенку, что реально воплощается при надежной наружной тепловой изоляции трубы. Соотношения для массоотдачи от стенки к пленке могут использоваться для описания теплоотдачи при нулевом потоке тепла на границе пленка - газ, что сложно реализуемо, особенно в области стабилизированного теплообмена. Однако эти результаты применимы для теплообмена между двумя параллельными пластинами с постоянной температурой, расположенными на расстоянии 2, и движущейся между ними средой. Тепловой поток через поверхность, равностоящую от обеих пластин, будет равен нулю из условия симметрии.

Массоотдача в турбулентной пленке. Рассмотрим массо­отдачу в области стабилизированного импульсо- и массообмена в турбулентной пленке, стекающей под действием силы тяжести по вертикальной стенке в режиме слабого взаимодействия с газом.

Начнем с массопередачи между стенкой и пленкой. Для нахождения коэффициента массоотдачи в пленке воспользуемся моделью турбулентного диффузионного пограничного слоя Ландау-Левича, предполагая, что все сопротивление массоотдачи сосредоточено в вязком подслое вблизи стенки, а вне его концентрация не меняется вдоль оси y. В соответствии с (7.139), (7.141), (6.137) и (6.151) получим

(7.190)

. (7.191)

Коэффициент трения Фаннинга для турбулентной пленки находится из соотношения (6.148) или (6.157). Учитывая, что Nu_г, определяется формулой (6.154), гидродинамическая аналогия массообмена в данном случае, на первый взгляд, отсутствует. Тем не менее приближенная гидродинамическая аналогия, как и для теплообмена в трубе, наблюдается. Соотношение (7.191) можно получить с использованием (6.76), справедливого как для плоского пограничного слоя, так и для трубы:

. (7.192)

Полагая Pr_g >>1, несложно из (7.192) получить (7.191). Если значение критерия Прандтля невелико, то следует пользоваться соотношением (7.192), в том числе и для теплообмена стенки с пленкой.

Рассмотрим теперь массопередачу между пленкой и газовой фазой. Для нахождения коэффициента массоотдачи в пленке также используем модель Ландау-Левича. При этом необходимо знать величину А в (7.138) для свободной поверхности. Она может быть определена из корреляции для D_т, рекомендованной в [26]:

, (7.193)

, (7.194)

. (7.195)

Для массоотдачи от границы газ - жидкость к турбулентной пленке в режиме слабого взаимодействия гидродинамическая аналогия, даже приближенная, отсутствует:

.

Итак, рассмотрена массоотдача в ламинарной безволновой и турбулентной пленке в режиме слабого взаимодействия с газом. При ламинарном волновом течении пленки 3 < Re_ < 300 коэффициенты массоотдачи от границы газ - жидкость к пленке оказываются большими по сравнению с величинами, найденными из соотношений для ламинарной безволновой пленки.

В режиме сильного взаимодействия движение газа оказывает влияние на массоотдачу в пленке. В случае прямотока увеличение скорости газа приводит к возрастанию скорости жидкости и коэффициентов массоотдачи. Для противотока наблюдается обратная картина. В режиме сильного взаимодействия, когда основным источником импульса в пленке становится сила трения с газом, а не сила тяжести (_ж,gg/^г_yx0), может наблюдаться приближенная гидродинамическая аналогия массоотдачи в пленке, разумеется, при идентичности граничных условий.