5.3.2. Турбулентный режим течения

Для труб круглого сечения переход от ламинарного режима к турбулентному начинается при Re_d > 2300, а для Re_d > 10⁴ реализуется развитое турбулентное течение. Результаты, которые будут получены в данном разделе, могут применяться при Re_d > 410³, т.е. справедливы для большей части переходной области и всего диапазона развитой турбулентности. Решим задачу определения полей скорости, давления и тензора напряжений (потока импульса), как и в случае ламинарного движения. Использовав координату y = R r, элемент тензора вязких напряжений (поток импульсаW_x в направлении r за счет молекулярного и турбулентного механизмов переноса), можно записать

. (5.74)

Далее в данном разделе не будут указываться индексы при обозначении . Основная сложность описания турбулентного движения заключается в отсутствии строгих теоретических соотношений для коэффициента турбулентной вязкости_т, который к тому же является функцией поля скорости. По аналогии с длиной свободного пробега молекул газа Прандтлем введено понятие пути смешения , характеризующее расстояние, на котором турбулентный вихрь, перемещаясь, сохраняет свою индивидуальность. С учетом этого

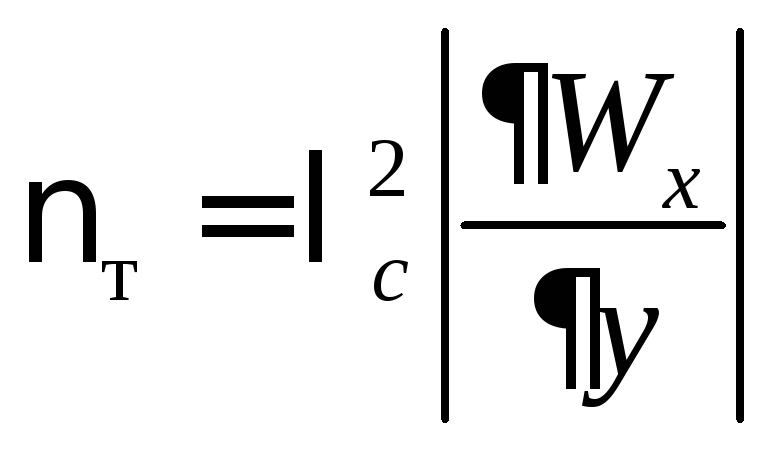. (5.75)

Рис. 5.8. Профиль скорости при турбулентном стабилизированном течении в цилиндрической трубе:

1 вязкий подслой; 1+2 пристенная область; 2+3 турбулентная область

Воспользуемся наиболее простой двухслойной моделью пристенной турбулентности Прандтля. Учитывая, что интенсивность турбулентных пульсаций от ядра потока к стенке снижается до нуля и в непосредственной близости от стенки преобладающим механизмом переноса импульса является молекулярный ( > _т), можно подразделить пристенную область (y << R) (y/R < 0,1) на две подобласти. В первой из них, называемой вязким (ламинарным) подслоем (y < _1,г), учитывается только молекулярный механизм переноса импульса, а во второй (y > _1,г) только турбулентный (рис.5.8). Поток импульса во всей пристенной области считается постоянным и равным потоку импульса на стенке  = const = _c. Для удобства записи вводится понятие динамической скорости , связанной простым соотношением с _c

. (5.76)

В вязком подслое толщиной _1,г можно интегрированием уравнения потока импульса найти поле скорости, определив константу интегрирования С₁ из граничного условия W_x = 0 при y = 0

, (5.77)

, , (5.78)

, , (5.79)

где безразмерная поперечная координата.

Для пристенной области вне вязкого подслоя (y > _1,г) длина пути смешения полагается прямо пропорциональной расстоянию от стенки. Тогда

, (5.80)

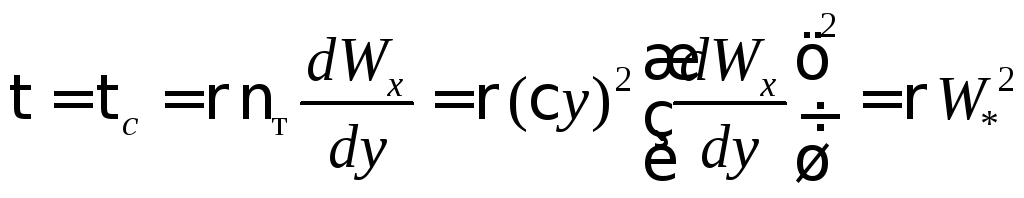, (5.81)

, (5.82)

. (5.83)

Постоянную С₂ можно определить из условия сопряжения выражений (5.83) и (5.79) для поля скорости на границе вязкого подслоя при :

, (5.84)

. (5.85)

Для получения явного вида поля скорости необходимо знание двух параметров , . Они могут быть определены непосредственно из эксперимента. Как следует из многочисленных опытных данных, найденный логарифмический профиль скорости (5.83), (5.85) является универсальным, т.е. справедлив для любыхRe_d > 410³ с постоянными значениями параметров  = 0,4; *_1,г = 11,6. Тогда окончательно для пристенной области имеем

; . (5.86)

Существуют и более сложные зависимости для поля скорости: трех - и четырехслойные модели. Мы же ограничимся рассмотрением простейшей. Экспериментальные данные свидетельствуют, что несмотря на зависимость потока импульса от радиуса трубы (  const) и невыполнение соотношения (5.80) для турбулентного потока вне пристенной области (r/R < 0,9), логарифмический профиль скорости (5.86) соблюдается вплоть до оси трубы (r = 0), где скорость W_x = W_x,max.

Можно связать локальную скорость W_x(r) c W_x,max:

, (5.87)

, . (5.88)

Используя соотношения (5.88) и (5.64), можно найти среднюю скорость турбулентного потока, пренебрегая отличием зависимости скорости в тонком вязком подслое от (5.88):

. (5.89)

Экспериментальным данным лучше, чем коэффициент 3,75, удовлетворяет коэффициент 4,08. Во все выражения для скорости входит динамическая скорость W_* или поток импульса на стенке _с, с учетом (5.76). Для замыкания решения необходимо выразить _с через среднерасходную скорость . Это можно сделать двумя способами: с использованием коэффициента трения Фаннингаи коэффициента импульсоотдачи (5.71):

. (5.90)

Проинтегрируем выражение для потока импульса (5.74) по поперечной координате от стенки до оси трубы:

, (5.91)

. (5.92)

Используя соотношения (5.89) и (5.50), перепишем

. (5.93)

Решим относительно , поделим наи разделим интеграл на две части, учитывая, что в вязком подслоеи перенос осуществляется только за счёт молекулярного механизма

. (5.94)

Величина, обратная , является сопротивлением переносу импульса. Из соотношения (5.94) видно, что оно аддитивно складывается из сопротивлений переносу импульса в вязком подслое и в турбулентной области. Последний член в (5.94) возникает вследствие использования в уравнении импульсоотдачи (5.71) средней, а не максимальной скорости. С использованием соотношений (5.81) и (5.50), а также учитывая распространение выражения (5.86) на всю турбулентную область, можно записать

, , (5.95)

, (5.96)

, (5.97)

, (5.98)

. (5.99)

Выразив  через из (5.71), (5.90) и подставив в (5.99), а также связав с помощью (5.76), (5.90) среднюю и динамическую скорости получим уравнение для определения коэффициента трения Фаннингаили коэффициента гидравлического сопротивления трению_г, учитывая, что для равномерного стабилизированного течения в трубе _г = 4,т.к.

, (5.100)

, (5.101)

, (5.102)

. (5.103)

Многочисленные опытные данные подтверждают возможность использования формулы (5.103) в диапазоне 410³ < Re < 10⁷ и говорят о лучшем согласии с экспериментом при замене коэффициента 0,91 на 0,8, что дает поправку для _г менее 4%. Некоторое неудобство соотношений (5.102) и (5.103) заключается в неявном виде зависимостей (Re_d) и _г(Re_d). Поэтому на практике часто используются эмпирические явные выражения для и_г, работоспособные в более узких интервалах чисел Re_d. Так заменив логарифмический профиль скорости (5.88) степенным с показателем 1/7, приемлемым для интервала 410³ < Re_d < 10⁵, можно получить соотношение, аналогичное эмпирической формуле Блазиуса (5.105), отличающейся лишь коэффициентом 0,343. Для лучшей сходимости с экспериментом результатов, найденных с использованием профиля скорости (5.104) вместо (5.88), необходимо несколько увеличить толщину вязкого подслоя (_1,г>11,6)

, (5.104) . (5.105)

или в критериальном виде

. (5.106)

Из (5.105) можно получить явное выражение для коэффициента импульсоотдачи и гидродинамического критерия Нуссельта

, (5.107) , (5.108)

Принципиально вопрос решен и в рамках двухслойной модели пристенной турбулентности Прандтля, справедливой и при Re_d > 10⁵. Задавшись значением среднерасходной скорости , можно, зная лишь диаметр трубы, кинематическую вязкость и плотность среды, определить поля скорости, давления и потока импульса, а также коэффициенты импульсоотдачи и трения:(5.53) (5.102) или _г (5.103), W_* (5.100), Re_* (5.98),  (5.99), _c (5.76) или (5.90) или (5.71), W_x (5.79), (5.86) или (5.79), (5.88),  (5.50), р (5.52).

На практике зачастую приходится решать и обратную задачу по перепаду давленийр определять среднерасходную скорость или расход, как по уравнению Гагена-Пуазейля для ламинарного движения. В этом случае алгоритм может быть следующим:

(5.52), W_* (5.76), Re_* (5.98), (5.102),(5.90). Конечное выражение можно представить в следующем виде:

. (5.109)

Найдем толщину вязкого подслоя:

. (5.110)

При увеличении критерия Re_d от 410³ до 10⁷ уменьшается отношение следующих величин: толщины вязкого подслоя и радиуса трубы _1,г/R от 0,08 до 610^-5 по (5.110); сопротивлений переносу импульса в вязком подслое и в турбулентной области от 2 до 0,5 по (5.96); максимальной и средней скорости в трубе от 1,3 до 1,15 по (5.89). Напомним, что для ламинарного течения. Участок гидродинамической стабилизации для турбулентного режима движения составляет.

Таким образом, решена задача гидродинамики и для турбулентного стабилизированного движения в цилиндрической гладкой трубе. Однако при этом уравнения движения (5.45) и неразрывности (5.46) пришлось дополнить соотношениями для _т в рамках модели пристенной турбулентности Прандтля.

На практике дело приходится иметь не только с гладкими, но и с шероховатыми трубами. Под шероховатостью понимают неоднородность поверхности, вид которой зависит от материала труб, способа их изготовления и эксплуатации. Степень шероховатости  (относительная шероховатость) характеризуют отношением средней высоты бугорков  (абсолютная шероховатость) к внутреннему диаметру трубы d. Для новых стальных труб , чугунных, у старых загрязненных труб значения достигают 2 мм.

При ламинарном режиме движения шероховатость труб практически не влияет на коэффициент трения _г. Для турбулентного режима можно выделить три области влияния шероховатости на гидравлическое сопротивление трубопровода. В области гладкого трения высота бугорков значительно меньше толщины вязкого подслоя  << _1,г , они плавно обтекаются потоком, и шероховатость не влияет на коэффициент трения _г. При увеличении Re_d в соответствии с (5.110) толщина вязкого подслоя уменьшается и становится соизмеримой с величиной абсолютной шероховатости (область смешанного трения). Вокруг бугорков начинается вихреобразование, что приводит к потерям энергии потока и дополнительному увеличению коэффициента трения _г, величина которого в области смешанного трения зависит от Re_d и . При дальнейшем увеличении критерия Рейнольдса толщина вязкого подслоя становится значительно меньше высоты бугорков  >> _1,г коэффициент трения _г практически перестает зависеть от критерия Re_d и определяется лишь шероховатостью труб (автомодельная область). На рис. 5.9

Рис. 5.9. Зависимость _г(Re_d) и Nu_г(Re_d) для гладких труб ( _________ ) и _г(Re_d, ) для шероховатых труб (- - -)

показана зависимость _г и Nu_г,d от Re_d для гладких труб, а также зависимость _г(Re_d, ) для шероховатых труб при трех значениях  в трубах с зернистой шероховатостью.

Все результаты получены в данном разделе при допущении о постоянстве теплофизических характеристик среды:  = const. Однако если движение сопровождается тепло или массоотдачей, то такие допущения неправомерны, так как и  становятся зависимыми от температуры или концентрации среды. В этом случае, во-первых, нельзя выносить их из-под дифференциального оператора в уравнении движения (2.55) и, во-вторых, необходимо решать его совместно с уравнением нестационарной конвективной теплопроводности (2.45) или диффузии (2.27), так как поля скорости, температуры и концентраций оказываются взаимозависимы. Аналитическое решение получить, как правило, не удается, и учет влияния тепло-массообмена на гидродинамику производится с помощью эмпирических поправочных множителей, приводимых в справочной литературе. Более подробно этот вопрос рассматривается в разделе 9.2.3.