13.4.2. Методика расчета извлечения двух компонентов из инертного газа однокомпонентным абсорбентом

Рассмотрим в качестве простейшего примера извлечение двух компонентов малой концентрации из трехкомпонентной газовой смеси однокомпонентным абсорбентом. Как и при абсорбции в бинарных смесях удобнее пользоваться относительными массовыми или мольными концентрациями распределяемых компонентов в инертах, так как расход последних по высоте колонны изменяться не будет, и рабочие линии будут иметь форму прямой линии:

, (13.26)

где G и L – это массовые либо мольные расходы инертного газа и абсорбента. Так как отношение одинаково для обоих поглощаемых компонентов, то их рабочие линии будут параллельными.

Уравнения равновесия при бесконечном разбавлении также будут линейными. Однако их угол наклона для различных компонентов может отличаться из-за различия коэффициентов распределения :

(13.27)

Коэффициенты распределения для газовых компонентов i и абсорбента А находится через коэффициенты Генри (12.59):

m_i,x = E_i,А /p, (13.28)

а для паровых (12.52) – с использованием давления насыщенного пара чистого компонента i при данной температуре , его коэффициента активностипри бесконечном разбавлении в абсорбентеА и давления в абсорбере p:

m_i,x = ()/p. (13.29)

Связь сm_i,x устанавливается в зависимости от способа выражения концентрации (относительные массовые или относительные мольные [9, 49]).

Пусть заданы: расход инертного газа G , начальные концентрации в нем компонентов 1 и 2 , конечная концентрация ключевого компонента. На абсорбцию поступает абсорбент с начальными концентрациями первого и второго компонентов. Изобразим надиаграмме (рис.13.22) равновесные линии, соответствующие уравнениям (13.27). Допустим, что коэффициент распределения первого компонента больше, чем второго:. Отложим на осиначальные концентрации соответствующих компонентов, а также конечную концентрацию первого компонента. Из условия

(13.30)

найдем максимальное значение , а из уравнения материального баланса по первому компоненту минимальный расход абсорбентаL_min:

(13.31)

(13.32)

Рис. 13.22. Изображение рабочих и равновесных линий ключевого «1» и второго распределяемых компонентов в процессе абсорбции при их бесконечном разбавлении в инертах.

Рабочий расход абсорбента примем в В раз больше минимального и определим из уравнения (13.31) , по двум точкам () проведем рабочую линию для компонента 1. Рабочую линию для компонента 2 построить не можем, так как не известныи. Единственное, что можно сказать о рабочей линии на данном этапе – это то, что она пройдет параллельно рабочей линии для первого компонента. Так как нахождение рабочей скорости и диаметра аппарата для многокомпонентной абсорбции производится точно также как и для бинарной, то мы остановимся только на определении его высоты, а также конечных концентраций компонента 2 в газовой и жидкой фазах,.

Расчет абсорберов с непрерывным контактом фаз. Рассмотрим сначала абсорберы с непрерывным контактом фаз (насадочные и пленочные). Для определения высоты такого абсорбера требуется найти поверхность контакта фаз F. Допущение бесконечного разбавления распределяемых компонентов позволяет легко определить эту поверхность из уравнения (13.23) с использованием (13.24), определив из уравнения (13.31) , а также рассчитав коэффициенты массоотдачи,и массопередачи(компонентом «3» в жидкой фазе является абсорбент, а в газовойинертный газ)

, (13.33)

где . (13.34)

Для определения итребуется решить систему уравнений (12.261) – (12.266) для компонента 2 с упрощениями (13.23), (13.24), рассчитав, тогда имеем следующую систему уравнений:

(13.35) (13.36)

(13.37)

где (13.38)

Четыре уравнения системы (13.35) – (13.38) содержат четыре неизвестных . Можно получить как аналитическое, так и численное решение этой системы. Найдяможно построить рабочую линию для второго компонента по точкамна рис. 13.22. В первом приближении, допустив нахождение средней движущей силы, как средней арифметической, а не средней логарифмической движущих сил массопередачи в верхнем и нижнем сечениях абсорбера, заменив соотношение (13.38) на (13.39), можно найти более простое аналитическое решение данной системы уравнений:

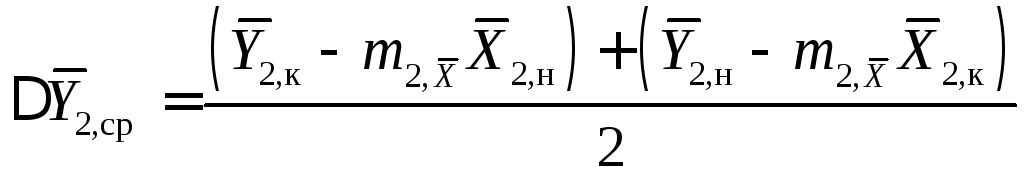(13.39)

Однако, если в полученном решении движущие силы массопередачи по второму компоненту в верхнем и нижнем сечениях аппарата будут отличаться более, чем в два раза доверять этому решению не следует. Более того при значительном изменении движущей силы массопередачи по второму компоненту величина может получиться отрицательной, то есть допущение (13.39) не приемлемо в этом случае.

Расчет абсорберов со ступенчатым контактом фаз. Рассмотрим аппарат со ступенчатым контактом фаз (тарельчатый). Для нахождения его высоты требуется определение числа тарелок N. Допущения, сделанные ранее, позволяют определить N методом потарелочного расчета, как и для бинарных смесей решая последовательно (12.267), (13.25) и (12.269) только для компонента 1. Например, от нижней тарелки () до выполнения условия. Предварительно следует определить эффективность по Мэрфри для первого компонента –. Эта величина не будет изменяться от тарелки к тарелке, так как допущение о бесконечном разбавлении позволяет считать неизменными все свойства газовой и жидкой фаз по всей высоте аппарата. Для определениятребуется решить систему 3N уравнений (12.267), (13.25) и (12.269) только для компонента 2, предварительно рассчитав . Неизвестными величинами будут являться:

.

Определить необходимое число тарелок можно и графически с помощью кинетической кривой. Для ее построения в рассматриваемом случае достаточно двух точек, так как она будет прямой линией. Из уравнения (13.25) найдем два значения , используя в качестве, и значение. Эти точки наносятся надиаграмму (рис. 13.23) и через них проводится кинетическая линия. Затем, вписывая прямоугольные ступени между рабочей и кинетической линиями, определим число действительных тарелокN, округляя, если необходимо, их число в большую сторону. Найти графическим способом величины сложнее. Для этого необходимо подобрать такое расположение рабочей линии, варьируяв уравнении (13.26), чтобы количество ступеней, вписанных между рабочей и кинетической линиями для второго компонента в интервалеравнялось найденному числу тарелокN. При выполнении этого условия находится графически приили из уравнения материального баланса для второго компонента аналогичного (13.31).

Рис. 13.23. Графические определения числа действительных тарелок и конечных концентраций второго компонента в процессе абсорбции при бесконечном разбавлении: кинетические линии.