ПРИЛОЖЕНИЯ

П.1. Некоторые сведения из области математики

П.1.1. Скаляры, векторы, тензоры

В учебнике использованы следующие обозначения величин: скаляры обозначаются обычными буквами (а); векторы буквами со стрелкой сверху (); тензоры буквами с волной сверху ().

Скаляр – величина, значение которой может быть выражено только числом. Скаляр задается одним числом.

Скалярное поле совокупность значений скалярной функции в каждой точке пространства. Например, (x,y,z) поле плотности, Т(x,y,z) поле температуры, с_i(x,y,z) поле концентрации и т.д.

Вектор величина, характеризующаяся модулем (длиной) и направлением. В декартовой системе координат вектор задается тремя числами проекциями на соответствующие оси :

,

где , , , единичные векторы, направленные вдоль осей x, y, z соответственно.

Вектор может быть представлен в виде строки или столбца:

или .

Векторное поле совокупность векторов в каждой точке пространства. Например, 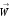(x,y,z) поле скорости, (x,y,z) поле потока вещества, (x,y,z) поле теплового потока и т.д.

Тензор второго ранга величина, характеризующаяся девятью числами, преобразующимися по определенному закону при переходе от одной системы координат к другой. В декартовой системе координат тензор второго ранга может быть представлен в виде матрицы размера 33 (см. П.1.5.):

.

Частными случаями тензора являются скаляры (тензоры нулевого ранга) и векторы (тензоры первого ранга). В дальнейшем термин “тензор” будет употребляться только по отношению к тензорам второго ранга.

Тензорное поле совокупность тензоров в каждой точке пространства. Например, (x,y,z) поле потока импульса (тензора напряжений).

П.1.2. Некоторые действия с величинами

Умножение скаляра на вектор – все проекции умножаются на скаляр (обладает свойством коммутативности):

.

Скалярное произведение векторов – перемножаются соответствующие проекции двух векторов и складываются (обладает свойствами коммутативности):

.

Тензорное произведение векторов (диада) – тензор, составленный из произведений элементов столбцов первого вектора и строк второго (свойством коммутативности не обладает):

.

Умножение скаляра на тензор – все элементы тензора умножаются на скаляр (обладает свойством коммутативности):

.

Умножение вектора на тензор – строка вектора умножается на соответствующий столбец тензора и произведения складываются, в результате чего получаются проекции нового вектора (обладает свойством коммутативности):

.

П.1.3. Дифференциальные операторы и их применение

Дифференциальный оператор Гамильтона 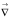(набла) является векторным оператором. Сам по себе он величиной не является и может использоваться только для обозначения операции с величиной, записанной справа от него, как и любая другая производная. В декартовой системе координат его можно представить в виде

.

Применение оператора к скалярным, векторным и тензорным функциям формально соответствует умножению вектора на соответствующую величину (см. П.1.2):

(градиент скаляра а);

(дивергенция вектора );

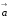(дивергенция тензора );

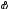(тензор градиента вектора ).

Дифференциальный оператор 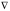² (оператор Лапласа) имеет вид

_.

Применение ² к скалярам и векторам формально соответствует умножению на соответствующую величину:

(лапласиан скаляра а),

(лапласиан

вектора ).

П.1.4. Символическая -функция Дирака

Символическая импульсная функция Дирака (х) определяется следующим образом:

где f(х) – произвольная функция, непрерывная в точке х = Х, а < b.

П.1.5. Матрицы и операции над ними

Прямоугольной матрицей [a_ij] размера mn называют совокупность скалярных элементов a_ij, расположенных в i-й строке и j-м столбце матрицы, содержащей m строк и n столбцов:

Матрица размера nn называется квадратной матрицей порядка n. Квадратная матрица называется диагональной [a_ii], если для всех ij a_ij = 0.

Матрица [a_i] размера m1 называется столбцом, матрица размера 1n – строкой.

Две матрицы размера mn [a_ij] и [b_ij] равны друг другу, если a_ij = b_ij для всех i и j.

Сумма двух матриц размера mn [a_ij] и [b_ij] есть матрица [c_ij] размера mn:

.

Произведение матрицы [a_ij] размера mn на скаляр b есть матрица [c_ij] размера mn:

.

Произведение матрицы [a_ik] размера mr на матрицу [b_kj] размера rn есть матрица [c_ij] размера mn:

.

При умножении двух матриц число столбцов первой матрицы должно равняться числу строк второй, каждый элемент c_ij есть сумма произведений элементов i-й строки первой матрицы на соответствующие элементы j-го столбца второй матрицы. Следует помнить, что даже если [a_ik] и [b_kj] – квадратные матрицы, то в общем случае

.

Отметим ряд полезных свойств:

;

;

;

;

;

;

;

;

.

Единичная матрица [I] порядка n есть диагональная матрица с единичными диагональными элементами. Для квадратной матрицы [a_ij] размера nn справедливо

.

Квадратная матрица [a_ij]^-1 называется обратной, если

,

.

A_ij – алгебраическое дополнение элемента a_ij в определителе det[a_ij]

,

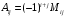где M_ij – минор элемента a_ij, т.е. определитель порядка (n–1), получающийся из определителя det[a_ij] вычеркиванием i-й строки и j-го столбца.

Определитель можно выразить через элементы произвольной его строки и столбца и их алгебраические дополнения:

.

Обратные матрицы обладают следующими свойствами:

;

;

.

Например,

,

где

.

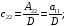
П.2. Выражения для потоков импульса и уравнения сохранения

субстанций в различных системах координат

П.2.1. Общий вид тензора вязких напряжений

В прямоугольной системе координат

;

;

;

;

;

.

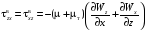В частном случае несжимаемой среды ( = const) из уравнения неразрывности (2.23) . Для плоскопараллельного равномерного движения в направлении оси х и .

В цилиндрической системе координат:

;

;

;

;

;

;

.

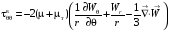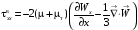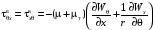П.2.2. Уравнения движения и неразрывности в цилиндрических

координатах

Уравнение движения:

В частном случае , = const, _т = 0 (уравнение Навье - Стокса):

Уравнение неразрывности:

.

П.2.3. Локальная форма закона сохранения энергии

в цилиндрических координатах

или ,

где

Если режим движения ламинарный и все теплофизические характеристики постоянны, то уравнение Фурье - Кирхгофа (2.46) будет иметь вид

.

П.3. Алгоритм расчета практической матрицы коэффициентов

многокомпонентной диффузии

П.3.1. Выражение для элементов матрицы коэффициентов многокомпонентной диффузии в среднеобъемной системе отчета

В рамках подхода независимой диффузии матрицу коэффициентов многокомпонентной диффузии в жидкой смеси можно выразить через эйнштейновские коэффициенты диффузии [89-91]:

.

где – символ Кронекера:

Для расчетов коэффициентов активности _i могут применяться модельные уравнения Вильсона, НРТЛ и т.д. [46].

Для газов умеренной плотности это выражение упрощается, так как коэффициенты активности _i=1, а парциальные объемы компонентов одинаковы V_i=idem

П.3.2. Расчет эйнштейновских коэффициентов диффузии

в газовых смесях

В газах умеренной плотности эйнштейновские коэффициенты диффузии могут определяться на основе молекулярных характеристик. Так, для сферически симметричного потенциала межмолекулярного взаимодействия Леннард-Джонса они могут быть найдены из выражения [89]

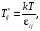
где k – постоянная Больцмана; – масса молекулы компонента i;  – параметры потенциала Леннард-Джонса, значения которых для ряда веществ приведены в [46], а также могут быть найдены по критическим параметрам [46] (– расстояние между молекулами, на котором (см. рис. 1.1), а – глубина потенциальной ямы); Т, p – температура и давление в системе; 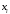– мольная доля компонента i; – функция, учитывающая отличие потенциала Леннард-Джонса от твердых сфер, удобная аппроксимация которой приведена в [46]; n – число компонентов смеси.

П.3.3. Расчет эйнштейновских коэффициентов диффузии

в жидких смесях

Для практического использования может быть применена приближенная формула [89,90], связывающая с коэффициентами бинарной диффузии при бесконечном разбавлении ():

.

По величинам имеется большой набор экспериментальных данных и полуэмпирических соотношений, например, Уилки-Ченга [9,46]:

, ,

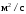где – мольная масса, кг/кмоль и коэффициент динамической вязкости растворителя, мПас; – коэффициент, учитывающий ассоциацию молекул растворителя; – мольный объем при нормальной температуре кипения чистого компонента i, см³/моль.

- 14 -