4.4 Уравнения массо-, тепло- и импульсопередачи

4.4.1. Локальная форма уравнений

В данном разделе рассматривается перенос субстанций из фазы I через межфазную поверхность в фазу II за счет молекулярного и турбулентного механизмов. Примем допущение о том, что сопротивлением переносу субстанций со стороны межфазной поверхности можно пренебречь. Это равносильно предположению об установлении равновесия на границе раздела фаз, тогда в соответствии с (1.10) можно записать

, ,. (4.89)

Используя обозначения разд. 4.1, проведем вывод уравнения массопередачи. Поскольку мы условились обозначать индексом I фазу, из которой происходит перенос субстанции, то > . Ось у направим от фазы I к II. С учетом вышесказанного запишем уравнения массоотдачи каждой из фаз (4.5), поделив их на соответствующие коэффициенты:

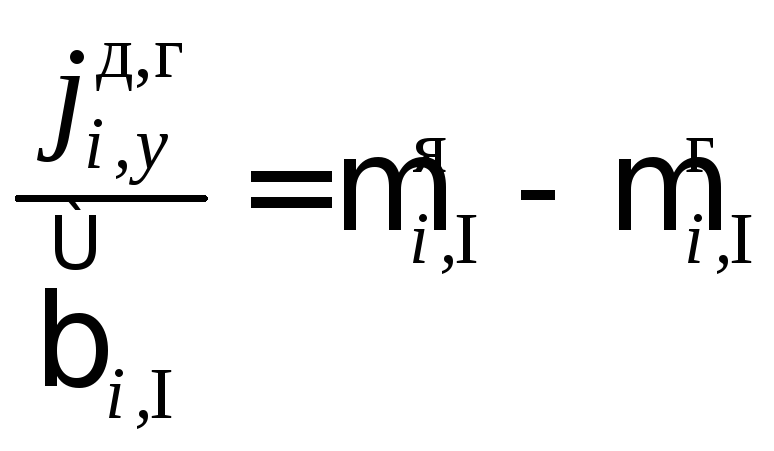, (4.90)

. (4.91)

Сложим эти два уравнения, имея в виду допущение (4.89), и решим относительно потока вещества компонента i через межфазную поверхность:

, (4.92)

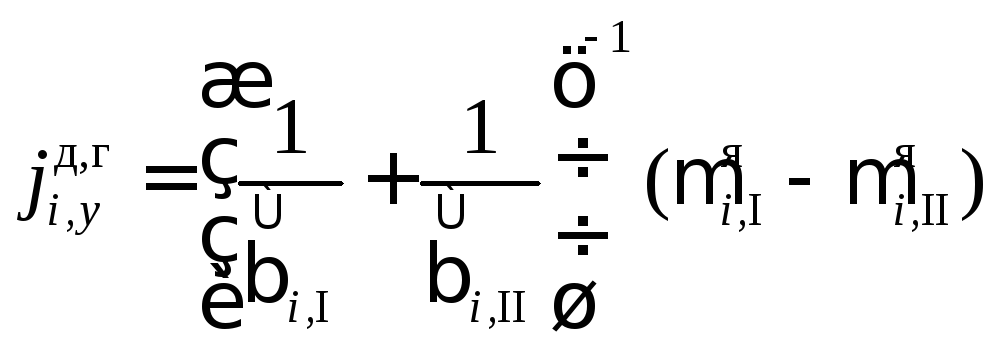. (4.93)

Уравнение (4.93) носит название уравнения массопередачи, а величина, стоящая перед разностью химических потенциалов в его правой части, называется коэффициентом массопередачи. Аналогичным образом могут быть получены уравнения тепло- и импульсопередачи, что позволяет использовать единую форму их записи:

, (4.94) , (4.97)

, (4.95) , (4.98)

, (4.96) , (4.99)

где , K_т, K_г коэффициенты массо-, тепло- и импульсопередачи, их смысл отличается от соответствующих коэффициентов (4.11)(4.14) лишь тем, что они характеризуют перенос субстанций из одной фазы в другую, а не внутри фаз. Движущими силами в данном случае являются разности соответствующих величин в ядрах двух фаз (или средних значений величин в фазах). Таким образом, уравнения (4.94)(4.96) имеют чрезвычайно простое содержание, что свидетельствует о пропорциональности межфазного потока субстанции отклонению системы от состояния равновесия. Для уравнения массопередачи в качестве движущей силы использована разность химических потенциалов компонента в фазах, позволяющая сохранить аналогию уравнений (4.94)(4.96). Подставить вместо_i в (4.94) концентрации с_i было бы ошибкой, так как равенство концентраций компонента в фазах не является условием равновесия, возможны процесс массопередачи при равенстве c_i,I^я = c_i,II^я и равновесие, т.е. отсутствие межфазного переноса, при c_i,I^я  c_i,II^я. Существует возможность представления движущей силы массопередачи через разность концентраций, однако это будет разность рабочей и равновесной концентраций компонента в одной из фаз.

Соотношения (4.97)-(4.99) можно переписать иначе:

, (4.100)

, (4.101)

. (4.102)

Величины, обратные рассмотренным кинетическим коэффициентам, носят название сопротивлений: 1/, 1/K_т, 1/K_г сопротивления массо-, тепло-, импульсопередачи (межфазные сопротивления), а1/, 1/, 1/ сопротивления массо-, тепло-, импульсоотдачи (фазовые сопротивления). Нетрудно видеть, что соотношения (4.100)(4.102) выражают аддитивность фазовых сопротивлений. Если не пренебрегать сопротивлением переносу субстанции со стороны межфазной поверхности, то к правым частям уравнений (4.100)(4.102) необходимо добавить соответствующие сопротивления. Например, если процесс теплопередачи осуществляется не при непосредственном контакте двух фаз, а через разделяющую их стенку, обладающую термическим сопротивлениемr_ст, то

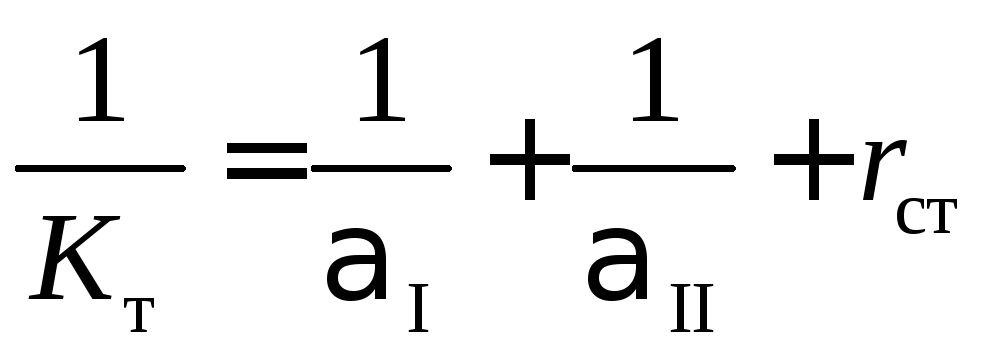. (4.103)

Вид уравнений (4.100) (4.102) свидетельствует, что больший вклад в межфазное сопротивление дает максимальное фазовое сопротивление. Если сопротивление первой фазы гораздо больше второй, то последним можно пренебречь, и в этом случае

; ;, (4.104)

т.е.

; ;, при,,. (4.105)

Интенсификация процессов химической технологии требует увеличения коэффициентов тепло- и массопередачи, т.е. уменьшения соответствующих сопротивлений. Исходя из вышесказанного, для этого в первую очередь необходимо уменьшать наибольшее фазовое сопротивление, т.е. увеличивать наименьший коэффициент массо- или теплоотдачи.

Отношения движущих сил массо-, тепло-, и импульсоотдачи в первой и второй фазах прямо пропорциональны отношению соответствующих фазовых сопротивлений, т.е. обратно пропорциональны отношению коэффициентов переноса в фазах. Докажем это на примере теплопередачи. Запишем уравнения теплоотдачи для каждой из фаз и поделим их на соответствующий коэффициент теплоотдачи:

, (4.106)

. (4.107)

Поделим уравнение (4.106) на (4.107):

. (4.108)

Профили химических потенциалов, температуры и скорости в процессах переноса субстанций через границу раздела фаз, не обладающую сопротивлением, приведены на рис. 4.3, а профиль температуры для процесса теплопередачи через стенку толщиной на рис. 4.4. В обоих случаях сопротивление в первой фазе больше, чем во второй.

Рис. 4.3. Профили химических потенциалов, температуры и скорости в процессах переноса субстанций через границу раздела фаз не обладающую сопротивлением: _г, _т, _д толщина гидродинамического, теплового и диффузионного пограничных слоев