4.3. Аналогия процессов массо-, тепло- и импульсоотдачи

Аналогия рассматриваемых процессов в широком смысле (см. разд. 2.4.3) обусловливается аналогией уравнений, составляющих исчерпывающее описание процессов переноса (2.27), (2.45), (2.55), а также аналогией уравнений массо-, тепло- и импульсоотдачи (4.5) (4.7), что позволяет упростить изучение этих процессов. Аналогия в узком смысле предоставляет возможность использовать результаты исследований процесса переноса одной субстанции для описания других. Однако при этом необходимо помнить об отсутствии полной аналогии процесса переноса импульса с переносом массы и тепла, вследствие векторной природы первой субстанции и скалярной двух других, а также наличия в уравнении движения (2.55) двух дополнительных членов, учитывающих влияние на перенос импульса массовых сил и внешнего давления. Аналогия может нарушаться при молекулярном массопереносе в многокомпонентных смесях за счет появления матрицы коэффициентов диффузии. Кроме того, для возможности использования уравнений подобия необходима идентичность не только дифференциальных уравнений, но и граничных условий. Применяя аналогию, также следует одинаковым образом выбирать характерные величины при определении движущих сил процессов массо-, тепло- и импульсоотдачи (разность граничных значенийс_i^г, , W_х^г и значений этих величин в ядре фазы (пограничный слой), средних по сечению (труба) или на внешней границе фазы (пленка) и т.д.).

Рассмотрим вначале аналогию процессов тепло- и массоотдачи. Поделив тепловой критерий Нуссельта на диффузионный (в данном разделе прилагательное «тепловой» во избежание путаницы будет использоваться) можно получить критерий, характеризующий это явление:

. (4.71)

В дальнейшем будем рассматривать аналогию в узком смысле слова. Она позволяет использовать результаты исследования одного из процессов для описания других и соблюдается при идентичности дифференциальных уравнений, граничных условий и движущих сил. В этом случае единственной причиной отличия полей температуры и концентраций, как это следует из уравнений Фурье-Кирхгофа и нестационарной конвективной диффузии, будет различие коэффициентов температуропроводности и диффузии. Учитывая однозначную связь полей температуры и концентраций с безразмерными коэффициентами тепло- и массоотдачи (Nu_т ,Nu_д ), можно сделать вывод, что и их отличие будет обусловлено той же причиной, тогда

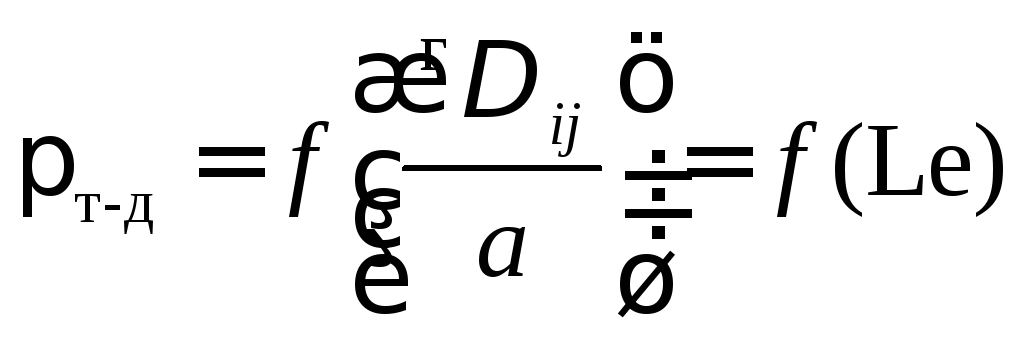, (4.72)

(критерий Льюиса). (4.73)

Имея в виду применяемую обычно степенную форму критериальных уравнений, можно представить зависимость (4.72) в виде

, . (4.74)

Для ламинарного движения показатель степени n зависит лишь от граничных условий. При турбулентном режиме к молекулярным коэффициентам температуропроводности и диффузии добавляются их турбулентные аналоги, что приводит к дополнительной зависимости n от критерия Рейнольдса и симплексов теплофизического подобия. При Re,, что понятно, так как _i ~ , ~ a^1-n . При больших Re, когда преобладает турбулентный механизм переноса, зависимость от коэффициентов молекулярного переноса уменьшается.

Таким же образом можно представить гидродинамическую аналогию процессов тепло- и массоотдачи

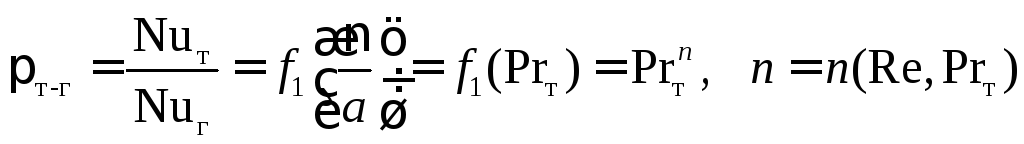, (4.75)

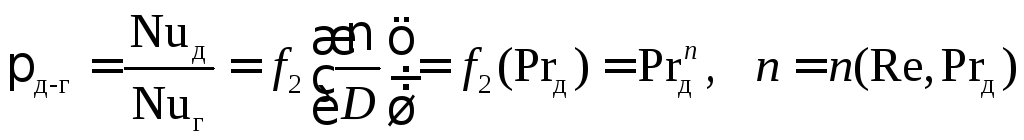. (4.76)

Нетрудно увидеть, что при равенстве, например, Pr_т = 1, достигается полная аналогия (аналогия Рейнольдса) процессов тепло- и импульсоотдачи, обусловленная идентичностью полей скорости и температуры _т-г = 1. Связь (4.74) (4.76) при наличии аналогии позволяет по известным уравнениям гидродинамического подобия и значениям показателя степениn определить коэффициенты тепло- и массоотдачи.

Так, для ламинарного пограничного слоя на плоской пластине с помощью известного из аналогии Чилтона-Кольборна, применимой в большом количестве случаев, значения n = 1/3, а также уравнения для Nu_г можно получить выражения для Nu_т и Nu_д:

, (4.77)

тогда , (4.78)

,

или . (4.79)

Однако следует еще раз напомнить, что использование соотношений (4.74)(4.76) возможно лишь при наличии аналогии в узком смысле слова. Так, например, для ламинарного стабилизированного течения в трубе отсутствует аналогия тепло- и импульсоотдачи. Это объясняется существенным влиянием градиента давления на поле скоростей. Аналогичного члена в уравнении Фурье-Кирхгофа нет, что при идентичных граничных условиях W_х^г = const, = const дает Nu_г = 8, Nu_т = 3,66 и не соответствует (4.75). Может нарушить аналогию и отличие граничных условий. Так, если рассмотреть теплоотдачу в трубе при  = const, а массоотдачу при j_i^г =const, то Nu_т =3,66, a Nu_д = 4,36, что не соответствует (4.74).

Изложенный выше подход к рассмотрению гидродинамической аналогии на основе соотношений (4.75), (4.76) является новым [18] и не отражен в учебной литературе. Его особенностями являются использование уравнения импульсоотдачи (4.7) и гидродинамического аналога критерия Нуссельта (4.49). На наш взгляд, он более удобен и прост для понимания. Тем не менее, по-видимому, необходимо изложить и традиционный подход.

Обычно поток импульса на границе раздела фаз (на стенке) записывают с использованием коэффициента трения Фаннинга, имея в виду, что W_х^г = 0 за счет эффекта прилипания:

; . (4.80)

Нетрудно убедиться, что при W_x^г = 0 коэффициенты уравнений (4.7) и (4.80) связаны простым соотношением

. (4.81)

Преимущества применяемого нами уравнения импульсоотдачи (4.7) состоят в следующем: единая форма уравнений массо-, тепло- и импульсоотдачи; линейная связь потока импульса с движущей силой; удобство анализа зависимости коэффициентов тепло- и массоотдачи от скорости движения, так как .

В традиционном подходе отсутствует аналогия описания переноса импульса с тепло- и массоотдачей, поэтому вводится критерий Стэнтона, характеризующий отношение потока субстанции на межфазной границе и конвективного потока в ядре фазы:

, (4.82)

, (4.83)

. (4.84)

Последнее соотношение (4.84) названия не получило и обозначено нами как гидродинамический критерий Стэнтона для лучшего выявления гидродинамической аналогии, которая может быть представлена в виде

, (4.85)

. (4.86)

Нетрудно установить связь использованных нами критериев _т-г и _д-г с соответствующими критериями Стэнтона, применяя (4.82)-(4.84):

, (4.87)

. (4.88)