4.2. Нахождение коэффициентов массо-, тепло- и импульсоотдачи, подобие соответствующих процессов

Вблизи границы раздела фаз даже при турбулентном режиме течения турбулентные пульсации затухают. Поэтому потоки субстанций через границу раздела фаз в отсутствие конвективного механизма переноса можно записать лишь с учетом молекулярного:

, (4.32)

, (4.33)

. (4.34)

Приравняв эти выражения уравнениям массо-, тепло- импульсоотдачи (4.5) - (4.7), получим

, (4.35)

, (4.36)

. (4.37)

Таким образом, для нахождения коэффициентов массо-, тепло- и импульсоотдачи нужно знать соответственно поля концентраций, температуры или скорости в непосредственной близости от границы раздела фаз, чтобы получить производные от них по координате y. Теоретически это можно сделать, решив систему дифференциальных уравнений, составляющих исчерпывающее описание процессов переноса в данной фазе. Другой способ, основанный на соотношениях (4.8) (4.10), требует знания зависимости относительных потоковj_i^*, q^*, ^* от координаты y, для нахождения которой также необходимо воспользоваться исчерпывающим описанием. Оба эти способа равноценны и могут выбираться из соображений удобства при решении конкретных задач. Начнем рассмотрение с процесса импульсоотдачи.

Допустим, что теплофизические характеристики фазы постоянны, движение ламинарное, в направлении оси z отсутствует конвективное перемещение среды W_z = 0, а также изменение скорости W_х температуры, концентрации и давления W_х/z = T/z = c_i/z =р/z = 0. Таким образом, трехмерная задача упрощается до двухмерной. Запишем систему уравнений Навье-Стокса (2.56) для такого случая, опустив верхние индексы «» для упрощения записи:

, (4.38)

. (4.39)

Дополним ее уравнением неразрывности для несжимаемой жидкости (2.23):

. (4.40)

Сформулировав граничные условия, содержащие, как правило, значение скорости в ядре потока W_х^я и ряд линейных размеров , необходимо решить эту систему дифференциальных уравнений для пограничного слоя, а если его выделить не удается, то для всего объема фазы. Однако даже с проделанными упрощениями получить точное решение не представляется возможным. Воспользуемся методом физического моделирования, позволяющим устанавливать связь между критериями подобия. Получим критерии гидродинамического подобия. Для этого поделим второй член уравнения (4.38) поочередно на остальные, отбрасывая операцию дифференцирования:

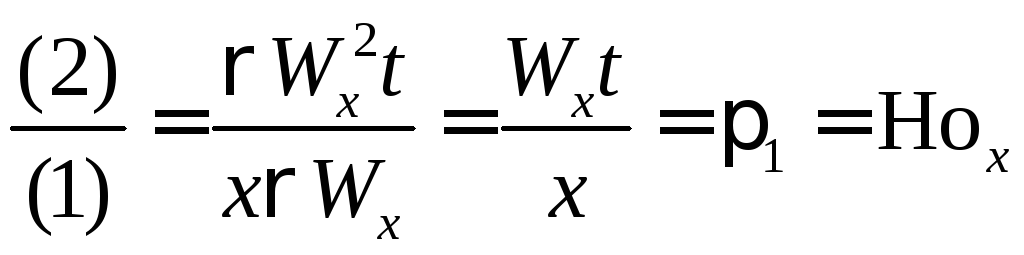(критерий гомохронности), (4.41)

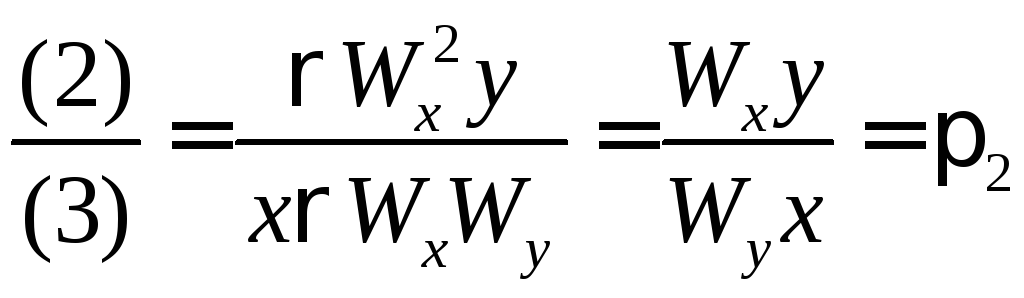, (4.42)

(критерий Рейнольдса), (4.43)

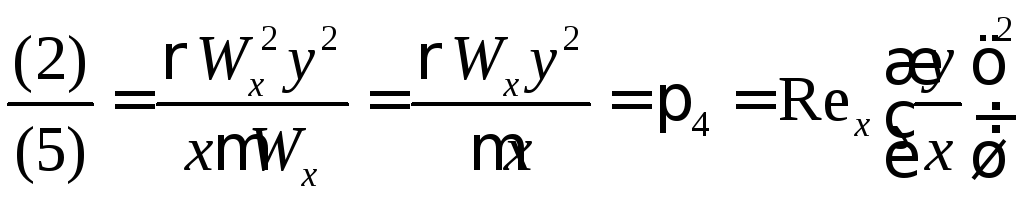, (4.44)

,

(критерий Эйлера), (4.45)

(критерий Фруда). (4.46)

Проделав аналогичную процедуру с уравнением (4.39), можно получить еще шесть критериев гидродинамического подобия _{7 12.} Последний критерий ₁₃ = ₂ найдем преобразованием уравнения (4.40). Для определения количества независимых критериев воспользуемся -теоремой Бэкингема (разд. 3.2.1). Число величин, между которыми необходимо установить зависимость,N=10(t, x, y, W_х, W_y, ,,р, g_х, g_у). Количество величин, обладающих независимыми размерностями n = 3, допустим (, W,). Количество величин, обладающих неодинаковой размерностью N_n=7(t, , W, ,,р, g). В этом случае минимальное количество критериев N_k = N n = = 10 3 =7, из них N_s= N N_n=10 7 = 3 могут быть симплексами подобия. Выберем четыре наиболее употребительных комплекса и три симплекса подобия, комбинацией из которых могут быть получены и остальные шесть. Тогда общее и частное решения системы дифференциальных уравнений (4.30) (4.40) могут быть представлены в виде

, (4.47)

,

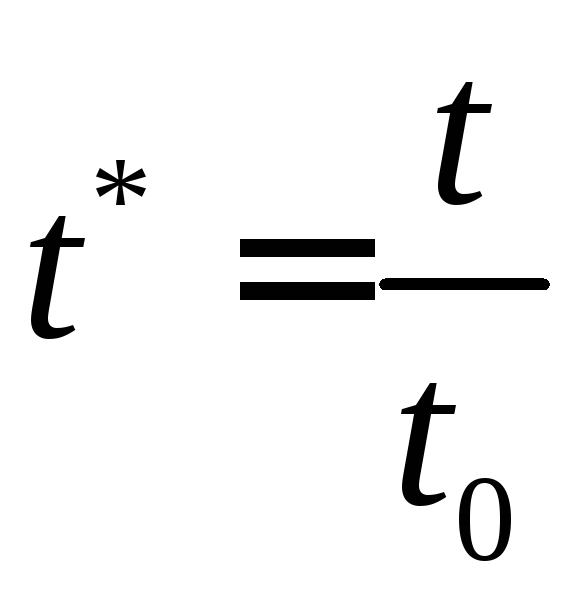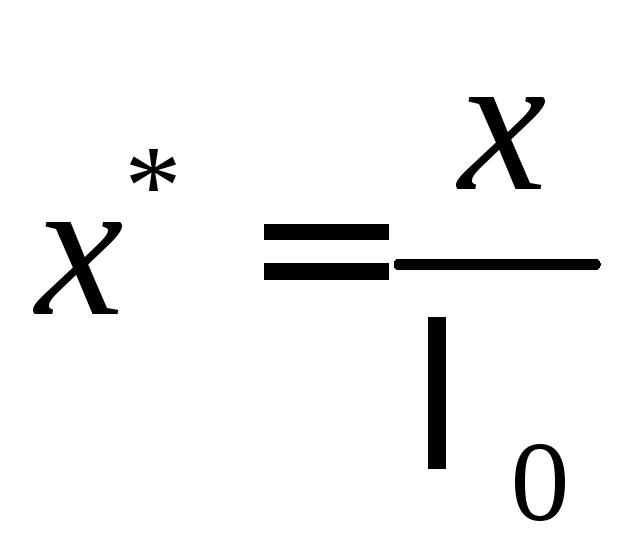; ; ; , (4.48)

где характерный линейный размер; характерный отрезок времени; критерии подобия без индексов – определяющие (составлены из величин, входящих в условия однозначности, например ).

Однако нас интересует коэффициент импульсоотдачи , который выражен посредством (4.37) через величины, входящие в уравнения (4.38) (4.40) и, соответственно, (4.47),(4.48). Поделив левую часть уравнения (4.37) на правую, можно привести его к безразмерному виду, получив гидродинамический аналог критерия Нуссельта:

. (4.49)

Поскольку поле скорости W_х по (4.37) однозначно определяет коэффициент , можно установить связь симплексаW_х/W_х^я с критерием Nu_г и представить решение следующим образом:

. (4.50)

Конкретный вид критериальной зависимости находится из опытных данных. Зная , по (4.49) можно определить. Поскольку на практике зачастую интерес представляет лишь средний поток импульса через границу раздела фаз, появляется возможность использования осредненных критериев, не замеряя значения величин во всех точках межфазной поверхности, что значительно упрощает экспериментальные исследования.

Если нас интересует осредненный по участку межфазной поверхности длиной L коэффициент импульсоотдачи , то для рассматриваемого случая интегрирование по dF от 0 до F по аналогии с (4.18) равносильно интегрированию по dx от 0 до L:

, (4.51)

. (4.52)

Остановимся на физическом смысле критериев гидродинамического подобия, который становится понятным из анализа отношений членов дифференциальных уравнений. Критерий Рейнольдса (Re) является мерой соотношения сил инерции и вязкого трения, критерий Эйлера (Eu) сил давления и инерции, критерий Фруда (Fr) сил инерции и тяжести. Критерий гомохронности (Но) характеризует нестационарность процесса переноса импульса. Гидродинамический критерий Нуссельта (Nu_г) является безразмерной формой коэффициента импульсоотдачи, смысл же его определяется выбором характерного линейного размера. Так, например, Nu_г,г характеризует вид зависимости W_х(y) в пограничном слое и при линейной зависимости Nu_г,г = 1 (в качестве характерного линейного размера использована толщина гидродинамического пограничного слоя).

Таким образом, определение коэффициентов импульсоотдачи с помощью метода физического моделирования состоит в экспериментальном установлении вида зависимости Nu_г от определяющих критериев на модельной установке и использовании этой зависимости для различных объектов при выполнении условий подобия. Для многих практически важных случаев число определяющих критериев в соотношениях (4.50) (4.52) может быть сокращено. Так, при расположении границы раздела фаз перпендикулярно направлению действия силы тяжести, g_х/g_у = 0, а влиянием g_у на W_х зачастую можно пренебречь и исключить критерий Фруда. Для стационарных процессов исключаются безразмерное время и критерий гомохронности. Процесс импульсоотдачи может стать автомодельным и по отношению к критерию Рейнольдса.

Перейдем к рассмотрению процесса теплоотдачи. Для этого в дополнение к уравнениям (4.38)-(4.40) необходимо записать уравнение Фурье - Кирхгофа (2.46). С учетом принятых допущений оно будет иметь вид

. (4.53)

Вследствие наличия в нем составляющих скорости W_х, W_у необходимым условием теоретического нахождения коэффициента теплоотдачи является предварительное решение системы уравнений (4.38) (4.40). Если же учитывать влияние температуры на плотность и вязкость среды, то требуется совместное решение системы уравнений (4.38) (4.40), (4.53). Поэтому в большинстве практических случаев для нахождения коэффициента теплоотдачи пользуются методом физического моделирования.

Из анализа системы уравнений (4.38) (4.40), (4.53) следует, что поля скоростей, давления и температуры могут быть описаны совокупностью 17 критериев подобия, четыре из которых в дополнение к уже имеющимся _{1 13} можно получить преобразованием (4.53). Для этого поделим 4-й член уравнения на остальные:

(критерий Фурье), (4.54)

,

(критерий Пекле), (4.55)

,

, (4.56)

. (4.57)

Поскольку искомой величиной при решении (4.53) является поле температуры, имеет смысл ввести определяемый симплекс подобия = Т/Т₀, в котором в качестве Т₀ может использоваться начальная или граничная температура. Частное решение по аналогии с (4.48) может быть представлено в виде

. (4.58)

Входящий в (4.47),(4.48) критерий гомохронности выражается через произведение критериев теплового подобия:

. (4.59)

Взяв отношение критериев Пекле и Рейнольдса, можно получить критерий Прандтля:

. (4.60)

Проанализируем смысл критериев теплового подобия. Критерий Пекле (Ре) показывает соотношение конвективного и молекулярного механизмов в переносе тепла. Критерий Фурье (Fo) характеризует нестационарность процесса теплообмена. Критерий Прандтля является симплексом теплофизического подобия и при идентичности уравнений (4.38), (4.53) и граничных условий характеризует подобие полей температуры и скорости.

Поделив левую часть уравнения (4.36) на правую, найдем выражение для теплового критерия Нуссельта, являющегося безразмерной формой коэффициента теплоотдачи:

. (4.61)

Поскольку поле температуры по (4.36) однозначно определяет коэффициент теплоотдачи, можно установить связь симплекса с критериемNu_т и представить ее в виде

. (4.62)

Как и в случае импульсоотдачи, возможно использование зависимости между осредненными критериями, а также ее упрощение при автомодельности процесса теплоотдачи по отношению к различным критериям.

Процесс массоотдачи в бинарных системах описывается соотношениями, аналогичными (4.53) (4.62). Отличие заключается в замене температуры концентрацией (Тс_i), а коэффициента температуропроводности коэффициентом бинарной диффузии (). Это обусловливается аналогией уравнений Фурье-Кирхгофа и нестационарной конвективной диффузии. Для отличия критериев подобия массообменных процессов от теплообменных к названию критерия добавляется прилагательное «диффузионный». Например, диффузионный критерий Фурье (Fo_д), диффузионный критерий Пекле (Ре_д), диффузионный критерий Прандтля, еще называемый критерием Шмидта (Рr_д  Sс), диффузионный критерий Нуссельта или критерий Шервуда (Nu_д  Sh). Для теплообменных процессов прилагательное «тепловой», как правило, опускается. Смысл диффузионных критериев подобия аналогичен тепловым:

, (4.63)

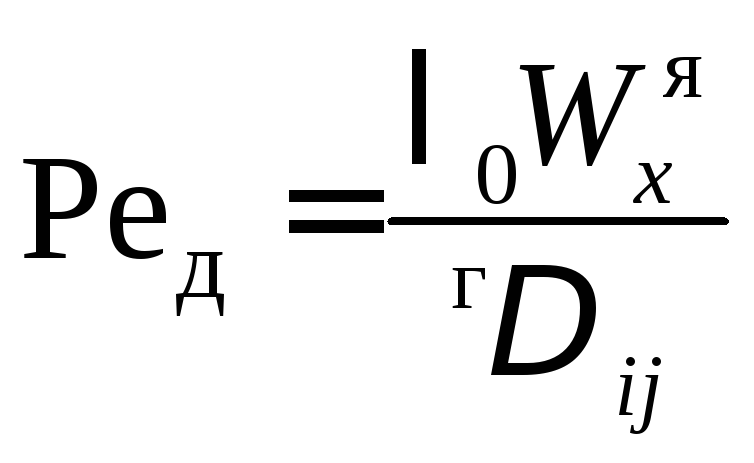, (4.64)

, (4.65)

. (4.66)

Рассмотрение подобия процессов импульсо-, тепло- и массоотдачи проводилось нами на примере ламинарного движения среды с постоянными теплофизическими свойствами. Наличие турбулентного механизма переноса, как уже отмечалось в разд. 3.5.3, не приводит к появлению новых критериев подобия, а лишь изменяет вид зависимости между ними.

Изменение теплофизических свойств среды, например, (р, Т, с_i) в газах, (T, c_i), (T, c_i), а(T, c_i) в жидкостях, накладывает дополнительное ограничение на метод физического моделирования. Для подобия в этом случае необходима идентичная зависимость каждого из свойств от соответствующих величин у модели и оригинала, только это позволит обеспечить подобие условий однозначности. Усложняется и вид критериальных соотношений. Так, например, при зависимости теплофизических свойств от температуры коэффициент теплоотдачи будет зависеть от разности температур (  ), а коэффициент импульсоотдачи от критериев теплового подобия и (  ).

В условиях неоднородной плотности среды действие силы тяжести приводит к естественной конвекции. Возникающую скорость движения определить бывает сложно, что затрудняет использование критериев Рейнольдса и Фруда. Для решения этой проблемы используют модифицированные критерии. Делением критерия Рейнольдса в квадрате на критерий Фруда может быть получен критерий Галилея:

. (4.67)

Умножение его на относительную разность плотностей среды в различных точках дает критерий Архимеда:

. (4.68)

Если разность плотностей вызвана неоднородностью температурного поля, то, связав их посредством коэффициента объемного расширения, критерий Архимеда можно преобразовать в критерий Грасгофа:

, (4.69)

. (4.70)

Таким образом, метод физического моделирования позволяет определить коэффициенты массо-, тепло- и импульсоотдачи с использованием критериальных уравнений, полученных обобщением опытных данных и приводимых в справочной литературе для различных условий проведения процессов.