15.1.3.4 Выбор флегмового числа

Для проведения процесса ректификации, в отличие от абсорбции, рабочие линии должны располагаться ниже линии равновесия, так как легколетучий компонент переходит из жидкой фазы в паровую. Это условие накладывает ограничение на флегмовое число, от величины которого зависит расположение рабочих линий. При уменьшении флегмового числа рабочие линии перемещаются вверх, что приводит к уменьшению движущейся силы процесса. В предельном случае при R=0 уравнение рабочей линии верхней части колонны, как это следует из (15.37), принимает вид , что соответствует горизонтали АЕ (рис. 15.23а). Это и понятно, так как при R=0 расход флегмы равен нулю (=0), следовательно, отсутствует орошение верхней части колонны и пары проходят по ней без взаимодействия с жидкостью не меняя своей концентрации (). Разумеется, такой режим работы колонны не рационален, так как верхняя часть колонны при этом не участвует в массообмене. На практике с такой ситуацией сталкиваться не приходится ибо ректификацию применяют для высокой степени разделения исходной смеси, а это значит, что по условию существенно выше и соотношение между ними, а также таково, что требует для достижения необходимой степени разделения нескольких теоретических тарелок в верхней части колонны. Это приводит к ограничению на флегмовое число, которое должно быть больше некоторого минимального значения (). Минимальное флегмовое число (как и минимальный расход абсорбента в процессе абсорбции) находится из условия соприкосновения линии равновесия с одной из рабочих линий, в этом случае становится равной нулю движущая сила массопередачи и процесс ректификации оказывается невозможным. Для смесей не сильно отличающихся от идеальных эта точка соприкосновения имеет координату (рис. 15.23б). Значение минимального флегмового числа в этом случае можно найти из условия равенства рабочей и равновесной концентраций , подставив последнюю величину в уравнение рабочей линии (15.37) и решив его относительно , получим

, (15.52)

. (15.53)

Рабочее флегмовое число должно быть больше минимального. При его увеличении рабочие линии приближаются к диагонали и совпадают с ней при , как это следует из уравнений (15.37), (15.41) (рис. 15.23в).

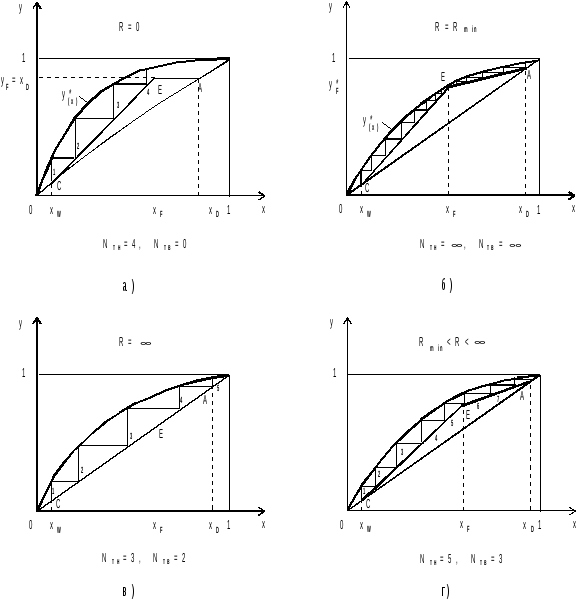
Рис. 15.23. Расположение рабочих линий при различных значениях флегмово-го числа и определение числа теоретических тарелок в нижней N_тн и верхней N_тв частях колонны

Проанализируем влияние флегмового числа на число теоретических тарелок N_т, необходимых для требуемой степени разделения исходной смеси. Воспользуемся для определения N_т графическим способом (см. раздел 13.7.3), заключающимся во вписывании прямоугольных ступеней между рабочими и равновесной линиями. Вписывание ступеней можно начинать как из точки С (нижнее сечение колонны), так и из точки А (верхнее сечение). Количество ступеней, расположенных между точками А и Е соответствует числу теоретических тарелок в верхней части колонны N_тв, а между точками С и Е - в нижней части N_тн. Число теоретических тарелок обычно округляют до целого значения в большую сторону. Общее число теоретических тарелок в колонне . Как видно из рисунка 15.23 , и , . Итак, число теоретических тарелок, а пропорционально им и число действительных тарелок N из (13.222), стремится к бесконечности при стремлении флегмового числа к минимальному значению, а это значит, что к бесконечности будет стремиться и высота колонны по (13.213). С другой стороны, при стремлении флегмового числа к бесконечности число теоретических тарелок и высота колонны будут минимальными, но зато к бесконечности будет стремиться расход пара в колонне по (15.36), а это приведет к бесконечно большим диаметру колонны и затратам на испарение жидкости в кипятильнике. Таким образом, предельные случаи явно не реализуемы и должна решаться задача выбора оптимального значения флегмового числа. В качестве критерия оптимальности обычно используют суммарные затраты на изготовление и функционирование ректификационной установки, которые в первом приближении можно разделить на два слагаемых. Одно из них пропорционально объему колонны (З₁), а другое - расходу испаряемой жидкости в кипятильнике (З₂).

, (15.54)

где коэффициент а зависит от стоимости материала колонны, ее монтажа и обслуживания, срока эксплуатации; в - от стоимости энергии (обычно греющего пара), используемой для испарения жидкости, удельной теплоты испарения, а также стоимости кипятильника и дефлегматора. Объем колонны V равен произведению высоты колонны Н на площадь поперечного сечения S. Первый из этих сомножителей пропорционален количеству тарелок N, а второй расходу пара и, следовательно, из (15.36) при фиксированном расходе дистиллята

, (15.55)

, (15.56)

Вид зависимостей затрат З, З₁ и З₂ от флегмового числа представлен на рисунке 15.24. Оптимальному флегмовому числу R_opt соответствует минимум затрат . Обычно для предварительных расчетов находят рабочее флегмовое число из эмпирических соотношений или задаются коэффициентом избытка флегмы _R в диапазоне 1.11.5, либо определяют R, обеспечивающее минимум функции , пропорциональной объему колонны.

. (15.57)

Рис. 15.24. Зависимость затрат от величины флегмового числа: З - суммарные затраты; З₁ - затраты, пропорциональные объему колонны; З₂ - затраты, пропорциональные расходу испаряемой в кипятильнике жидкости.