
11073
.pdf
нормально к срединной поверхности, сдвигающие силы Т отсутствуют. Поэтому для десяти составляющих усилий (2. 1) имеем:
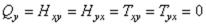 .
.
Остаются лишь усилия, указанные на рис. 50, причем усилия Nу и My при переходе от одного радиального сечения к другому не получают приращения. Из шести уравнений равновесия три превращаются в тождества. Остальные три запишутся так:
(2.13) |
|
|
(2.14) |
|
(2.15) |
На основании уравнения (2.13) можно заключить, что |
т. е. продольная сила Nx |
постоянна. В частности, она может равняться нулю при отсутствии у цилиндрической оболочки торцовых днищ.
Уравнение (2.14) после замены |
, сокращения двойки в первом члене и |
|
всех членов на |
примет вид |
|
|
. |
(2.16) |
В уравнении (2.15) второй член высшего порядка малости может быть отброшен. Тогда после сокращения на  оно примет вид:
оно примет вид:
. |
(2.17) |
Это уравнение показывает, что установленная для стержней зависимость между поперечной силой и изгибающим моментом справедлива и в отношении к рассматриваемой оболочке. Подставив эту зависимость в формулу (2.16) и перейдя от частных производных к полным дифференциалам, ввиду того, что осталась единственная
переменная х, получим |
|
. |
(2.18) |
Уравнение (2.18) содержит два неизвестных: Ny и Мx, поэтому для их нахождения необходимо еще одно уравнение, которое составляется исходя из известной величины
продольной силы |
|
. |
(2.19) |
От дифференциального уравнения (2.18) в усилиях перейдем к дифференциальному уравнению в радиальных перемещениях w. Для этого усилия выразим через деформации,
а деформации − через перемещения. |
|
На основании закона Гука (1.20) при |
= 0 |
(2.20)
50
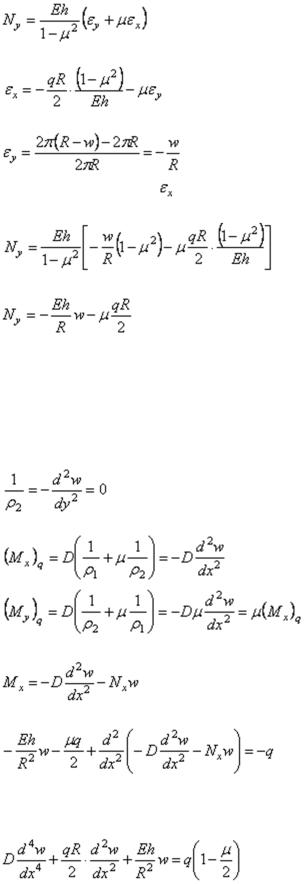
|
. |
(2.21) |
|
Приравняв правые части уравнений, найдем: |
|
||
|
. |
(2.22) |
|
Относительная окружная деформация |
|
|
|
|
. |
(2.23) |
|
Подставив значения |
из формулы |
(2.22) |
в (2.21), используя (2.23), получим |
выражение для продольной силы
,(2.24)
а после раскрытия скобок
. (2.25)
Изгибающие моменты, выраженные через перемещения w, определим с учетом дополнительного момента (Мх)Nx = Nw, который дает продольная сила:
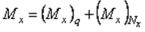 .
.
Так как при равномерном радиальном сжатии поперечное сечение цилиндра остается круговым, радиальное перемещение w одинаково во всех точках окружности и кривизна изогнутой срединной поверхности в экваториальном направлении от изгиба
Поэтому изгибающие моменты от поперечной нагрузки q
, |
|
(2.26) |
|
, |
(2.27) |
а изгибающий момент |
|
|
. |
(2.28) |
|
Подставим найденные значения (2.25) и (2.28) в уравнение (2.18):
.
Группируя члены, меняя знаки, учитывая выражение (2.19) и считая, что D − постоянная величина, получаем дифференциальное уравнение равновесия элемента цилиндрической оболочки в перемещениях
. (2.29)
Продольная сила Nx влияет на величину перемещения w незначительно, поэтому, пренебрегая ею, вместо формулы (2.23) на основании (2.26) имеем
51
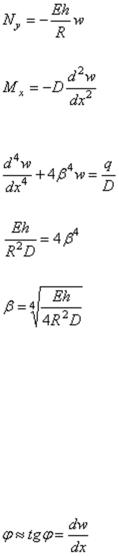
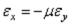 ;
;
вместо формулы (2.25)
, |
(2.30) |
и вместо формулы (2.28) |
|
. |
(2.31) |
Тогда приближенное дифференциальное уравнение равновесия элемента
цилиндрической оболочки в перемещениях |
|
. |
(2.32) |
В уравнении (5.31) введено обозначение
.
Величина
называется коэффициентом затухания перемещений. Она показывает, насколько затухают перемещения по мере удаления от места приложения усилия.
Расчет цилиндрической оболочки, как точный с помощью формулы (2.29), так и приближенный с помощью формулы (2.32), дает близкие результаты. Поэтому в дальнейшем будем пользоваться уравнением (2.32). Если проинтегрировать его и получить приближенное уравнение изогнутой срединной поверхности оболочки w = f (x) (без учета влияния продольной силы Nх), то все усилия и перемещения, характеризующие напряженно деформированное состояние оболочки, получатся по формуле (2.19), (2.30), (2.31) (2.27) и (2.17).
Угол наклона касательной к изогнутой срединной поверхности
.
Следует иметь в виду, что знаки в перечисленных формулах предусматривают внешнее радиальное давление q. При внутреннем давлении знаки должны быть изменены на обратные.
Интеграл дифференциального уравнения (2.32) складывается из интеграла однородного уравнения и частного решения уравнения; он может быть представлен с помощью показательных функций в виде
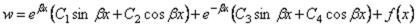 . (2.33)
. (2.33)
или, если заменить показательные функции гиперболическими на основании зависимостей
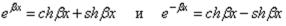 ,
,
в виде
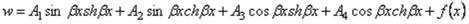 . (2.34)
. (2.34)
В выражениях (2.33) и (.34) f(х) − частное решение дифференциального уравнения (2.32). В случае радиальной нагрузки интенсивностью q, равномерно распределенной по поверхности оболочки, частное решение f(х), имеет вид
52
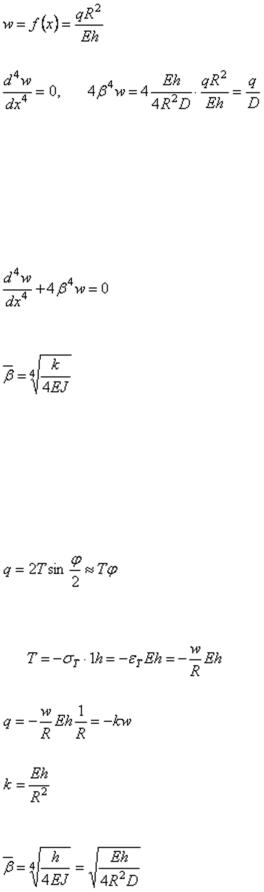
. |
(2.35) |
При этом
,
и уравнение (2.32) при подстановке в него решения (2.35) превращается в тождество. Коэффициенты С1, . . ., С4 и А1, . . ., А4 представляют собой произвольные постоянные, определяемые из граничных условий. Если усилия и перемещения на одном конце цилиндрической оболочки не влияют на усилия и перемещения, возникающие на другом конце, оболочка считается длинной. Если эти факторы влияют друг на друга, то оболочка
считается короткой.
Если в дифференциальном уравнении (2.32) принять правую часть равной нулю (при отсутствии радиальной нагрузки q), то оно примет вид
. |
(2.36) |
Уравнение (5.36) представляет собой уравнение балки на упругом основании, в нем
принято обозначение |
|
, |
(2.37) |
где k − коэффициент постели, связывающий интенсивность реакции основания q с прогибом балки w:
q = -kw.
Вследствие аналогии между уравнениями (2.32) и (2.36) полоску шириной, равной единице, вырезанную из цилиндрического сосуда вдоль образующей, можно рассматривать как балку на упругом основании и использовать все решения, применяемые при расчете такой балки, для расчета цилиндрической оболочки. При этом реакция основания
,
что следует из рис. 51.
Для полоски шириной, равной единице, центральный угол дуги 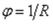 , а сжимающие
, а сжимающие
силы |
. |
Поэтому |
|
.
Следовательно,
и коэффициент (2.37), если заменить в его выражении жесткость балки EJ цилиндрической жесткостью D,
представляет собой коэффициент затухания перемещений.
53
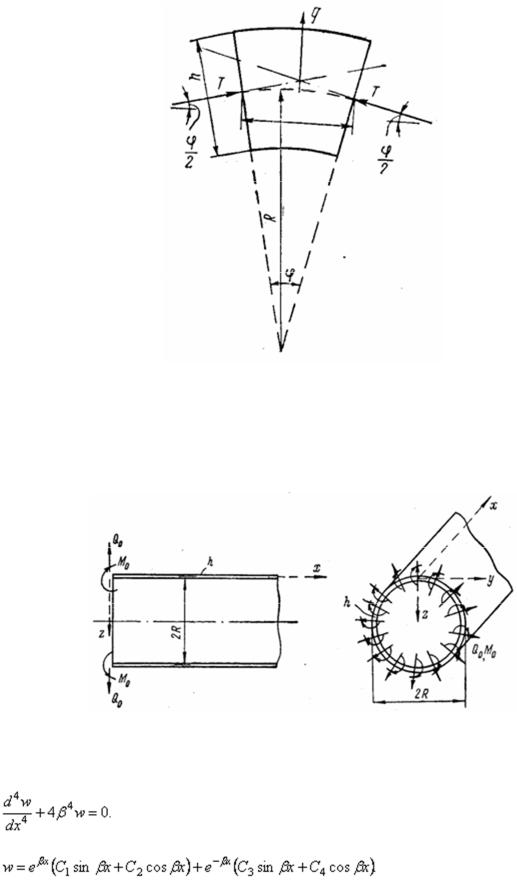
Рис. 51
2.5 Определение усилий и перемещений в длинной цилиндрической оболочке
Расчетный случай 1. Длинная оболочка с круглым поперечным сечением нагружена погонными изгибающими моментами M0 и погонными поперечными силами Q0 по торцу при х = 0 (рис. 52).
Рис. 52
Интенсивность радиальной нагрузки равна нулю, и поэтому дифференциальное уравнение (2.32) будет однородным:
Интеграл его не содержит частного решения и имеет вид
(2.38)
Усилия M0 и Q0 вызывают местный изгиб, радиальные перемещения быстро затухают и одно из условий для определения произвольных постоянных C1, . . ., С4 можно записать
54
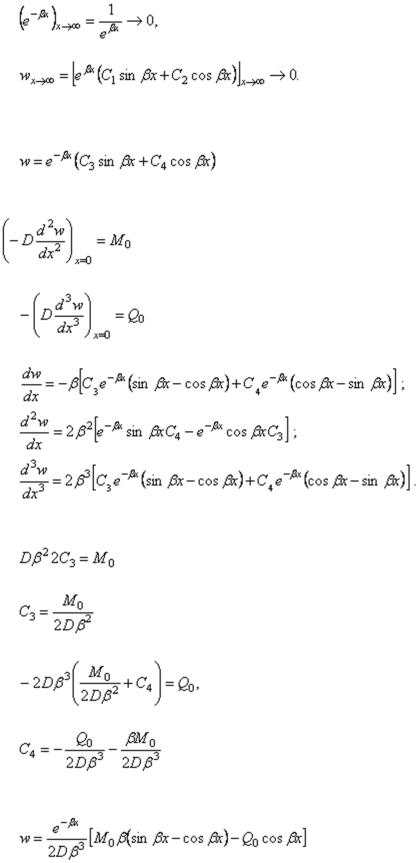
так: 1) при 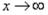
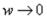 . Еще два условия можно записать для нагруженного торца: 2) при х = 0 Мx = М0 3) при х = 0 Qx = Q0 . Четвертого условия, как увидим, не понадобится.
. Еще два условия можно записать для нагруженного торца: 2) при х = 0 Мx = М0 3) при х = 0 Qx = Q0 . Четвертого условия, как увидим, не понадобится.
Действительно, при 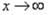
поэтому на основании первого условия получим
(2.39)
Чтобы это условие соблюдалось, круглая скобка должна быть равна нулю. Синус и косинус одновременно быть равными нулю не могут, следовательно, условие (2.39) возможно, только если С1 = С2 = 0. Тогда уравнение (2.38) принимает вид
(2.40)
и для определения двух постоянных С3 и С4 достаточно двух условий: второго и третьего. Из второго условия найдем:
(2.41)
и на основании формулы (5.17)
. (2.42)
Вычислим производные по х от выражения (5.40) для перемещения w:
(2.43)
(2.44)
(2.45)
Произвольную постоянную C3 найдем, подставив выражение (2.44) в условие (2.41). Учитывая, что синус нуля равен нулю, косинус − единице, а е0 = 1, получим
откуда
. |
(2.46) |
Подставив это выражение С3 в выражение (2.45), найдем из уcловия (2.42)
откуда |
|
. |
(2.47) |
Подстановка значений (2.46) и (2.47) в формулу (2.40) дает уравнение изогнутой срединной поверхности оболочки
. (2.48)
55

Подставив выражения (2.46) и (2.47) в формулы (2.43), (2.44) и (2.45), получим
(2.49)
(2.50)
(2.51)
Введем для комбинаций показательной и тригонометрической функций 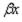 , входящих в уравнения (2.48) − (2.41), следующие обозначения:
, входящих в уравнения (2.48) − (2.41), следующие обозначения:
. |
(2.52) |
Тогда радиальное перемещение |
|
, |
(2.53) |
а его производные |
|
Имея выражения для перемещения w и его производных, можно, пользуясь соответствующими формулами, получить все усилия и перемещения в оболочке, в частности:
− угол наклона касательной к оси х
(2.54)
− изгибающий момент в меридиональном сечении
(2.55)
− поперечную силу в меридиональном сечении
. |
(2.56) |
Для входящих в эти формулы функций |
(2.22) в таблице 1 приведены численные |
значения безразмерных величин 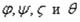 в зависимости от
в зависимости от 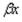 . При
. При 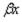 > 0 все четыре функции по абсолютной величине меньше единицы. По мере возрастания х эти функции
> 0 все четыре функции по абсолютной величине меньше единицы. По мере возрастания х эти функции
затухают, что подтверждает местный характер усилий и перемещений. При 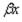 = 0 (а
= 0 (а
56
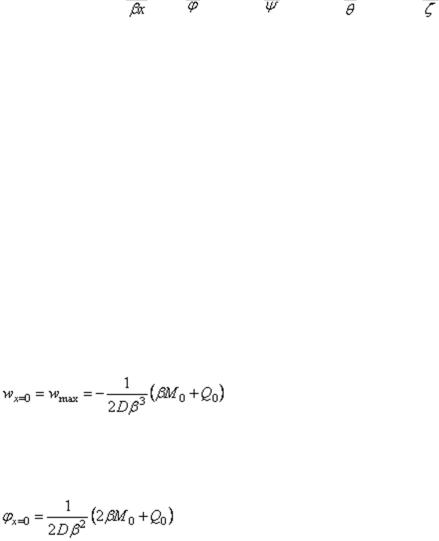
значит, и при х = 0), функции 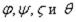 равны единице, а функция
равны единице, а функция 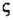 равна нулю. Поэтому на торце цилиндрической оболочки:
равна нулю. Поэтому на торце цилиндрической оболочки:
Таблица 1
|
|
|
|
|
0,0 |
+ 1,0000 |
+ 1,0000 |
+ 1,0000 |
+ 0,0000 |
0,1 |
+ 0,9907 |
+ 0,8100 |
+ 0,9003 |
+ 0,0903 |
0,2 |
+ 0,9651 |
+ 0,6398 |
+ 0,8024 |
+ 0,1627 |
0,3 |
+ 0,9267 |
+ 0,4888 |
+ 0,7077 |
+ 0,2189 |
0,4 |
+ 0,8784 |
+ 0,3564 |
+ 0,6174 |
+ 0,2610 |
0,5 |
+ 0,8431 |
+ 0,2415 |
+ 0,5323 |
+ 0,2908 |
0,6 |
+ 0,7628 |
+ 0,1431 |
+ 0,4530 |
+ 0,3099 |
0,7 |
+ 0,6997 |
+ 0,0599 |
+ 0,3708 |
+ 0,3199 |
0,8 |
+ 0,6354 |
- 0,0093 |
+ 0,3131 |
+ 0,3223 |
0,9 |
+ 0,5712 |
- 0,0657 |
+ 0,2527 |
+ 0,3185 |
1,0 |
+ 0,5083 |
- 0,1108 |
+ 0,1988 |
+ 0,3096 |
1,5 |
+ 0,2384 |
- 0,2068 |
+ 0,0158 |
+ 0,2226 |
2,0 |
+ 0,0667 |
- 0,1794 |
- 0,0563 |
+ 0,1231 |
2,5 |
- 0,0166 |
- 0,1149 |
- 0,0658 |
+ 0,0491 |
3,0 |
- 0,04226 |
- 0,05632 |
- 0,04929 |
+ 0,00703 |
4,0 |
- 0,02583 |
+ 0,00189 |
- 0,01197 |
- 0,01386 |
5,0 |
- 0,00455 |
+ 0,00837 |
+ 0,00191 |
- 0,00646 |
− радиальное перемещение по формуле (2.53) |
|
, |
(2.57) |
где знак минус показывает, что при принятых за положительные усилия М0 и Q0 (см. рис. 52) и оси z, направленной по радиусу к центру кривизны, перемещение w происходит от центра (радиус R увеличивается);
− угол наклона касательной по формуле (2.54)
; |
(2.58) |
− изгибающий момент Мх и поперечная сила Qx при х = О по формулам (2.55) и (2.56) получаются равными заданным на кромке величинам М0 и Q0.
Расчетный случай 2. Оболочка нагружена радиальными погонными усилиями Р, распределенными по окружности в сечении х = 0 (рис. 53). Начало координат выбираем в сечении, в котором приложена радиальная нагрузка. Для каждой половины оболочки слева и справа от начала координат можно применить решение, полученное для расчетного случая 1.
57
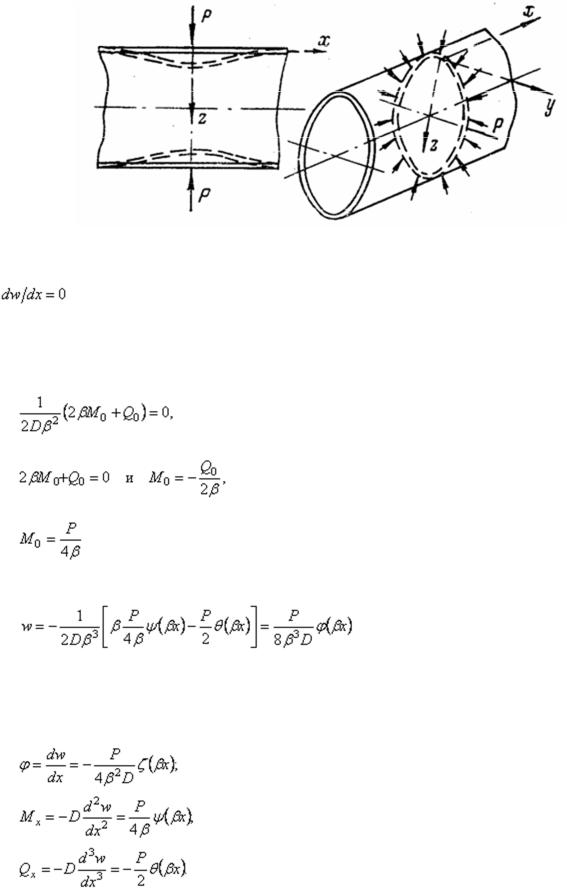
Рис. 53
Граничные условия для определения произвольных постоянных следующие: 1) х = 0,
(касательная в месте приложения силы, вследствие симметрии изгиба
оболочки, горизонтальна); 2) х = 0, 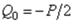 (погонная поперечная сила Q0 в начале координат равна половине радиальной нагрузки). Положительные направления изгибающего момента и поперечной силы показаны на рис. 52.
(погонная поперечная сила Q0 в начале координат равна половине радиальной нагрузки). Положительные направления изгибающего момента и поперечной силы показаны на рис. 52.
Пользуясь первым условием и формулой (2.58), находим
откуда |
|
|
или, учитывая второе условие, |
|
|
. |
(2.59) |
|
Подставив значения Q0 из второго условия и М0 из формулы (2.59) в формулу (2.53), |
||
получим уравнение радиальных перемещений |
|
|
|
, |
(2.60) |
так как |
|
|
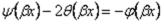 .
.
Продифференцировав выражение (2.60), определим в функции 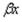 угол наклона касательной
угол наклона касательной 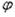 , изгибающий момент Мx и поперечную сил Qx
, изгибающий момент Мx и поперечную сил Qx
(2.61)
(2.62)
(2.63)
58
Так как функции 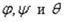 имеют наибольшее значение, равное единице при
имеют наибольшее значение, равное единице при 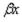 и х
и х
равных нулю, а функция 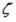 при этом равна нулю, то
при этом равна нулю, то
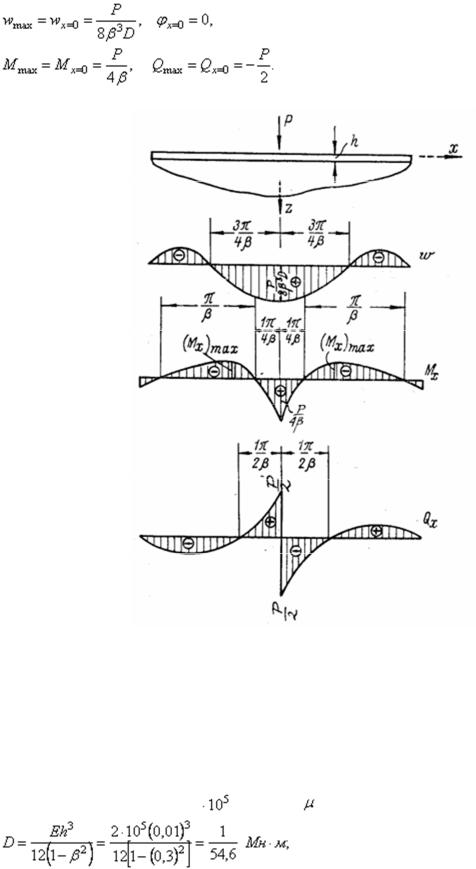
Эпюры w, Mx и Qx показаны на рис. 54.
Рис. 54
Видно, что ординаты эпюр быстро убывают по мере удаления от сечения х = 0, в
котором приложена радиальная нагрузка. При 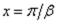 можно считать, что усилия и
можно считать, что усилия и
деформации пренебрежимо малы. Поэтому при длине оболочки 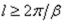 можно полагать, что усилия и перемещения на одном конце не влияют на эти факторы на другом конце. Такие оболочки относятся к длинным оболочкам.
можно полагать, что усилия и перемещения на одном конце не влияют на эти факторы на другом конце. Такие оболочки относятся к длинным оболочкам.
Чтобы оценить величину l, подсчитаем ее при таких данных:
R = 0,5 м; h = 1 см; E = 2 |
Мн/м2; |
= 0,3; |
59
