
11073
.pdf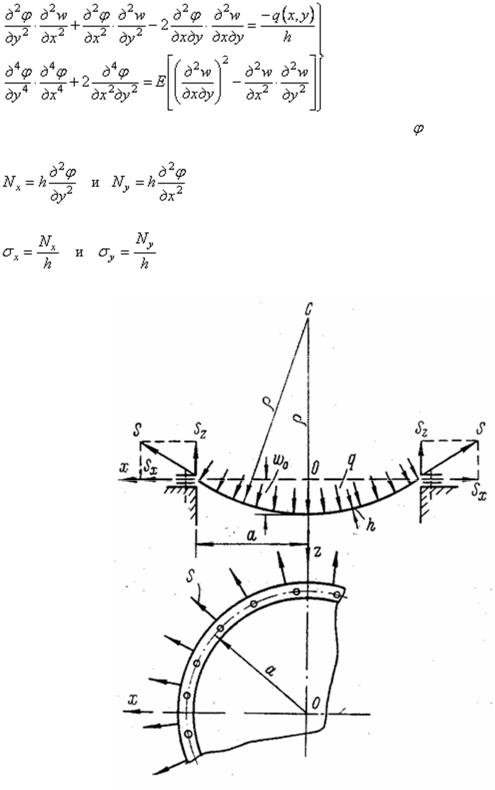
. |
(1.53) |
|
Уравнения (1.53) решаются приближенно. Если функция |
найдена, выражения для |
|
растягивающих цепных усилий Nx и Ny в мембране могут быть вычислены по формулам
, |
(1.54) |
а соответствующие цепные напряжения найдены из выражений
.
Рис. 34
Изгибающие и крутящие моменты, а также перерезывающие силы и соответствующие им напряжения в мембране отсутствуют.
30
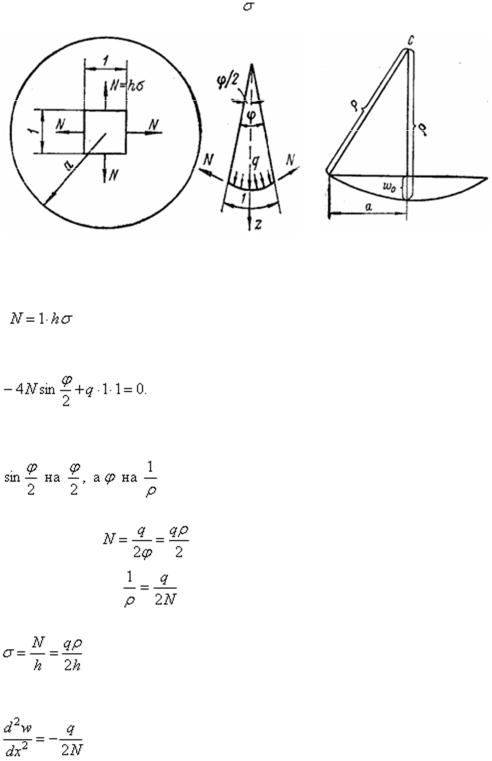
1.9 Приближенное определение прогиба и напряжений в круглой мембране
При выводе приближенных формул предполагается, что защемленная на контуре мембрана радиусом а и толщиной h (рис.34) изгибается, образуя шаровую поверхность, и
что нагрузка q действует по нормали |
к этой изогнутой поверхности. |
При |
этих |
условиях усилия N и напряжение |
(рис. 35,а) |
|
|
а |
б |
|
|
Рис. 35
по кромкам элемента, вырезанного из мембраны двумя взаимно перпендикулярными сечениями, окажутся одинаковыми. При размерах элемента, равных единице,
. |
(1.55) |
Согласно уравнению равновесия сумма проекций нагрузки и усилий, действующих по кромкам элемента на нормаль z к поверхности элемента
(1.56)
Центральный угол 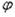 выражаем через длину дуги кромки элемента и радиус кривизны
выражаем через длину дуги кромки элемента и радиус кривизны
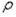 . Замена в уравнении (1.56), ввиду малости
. Замена в уравнении (1.56), ввиду малости 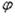 ,
,
дает выражение: |
|
|
− для усилия |
|
; |
− для кривизны |
. |
(1.57) |
Тогда для напряжения из формулы (1.55) получим |
||
. |
|
(1.58) |
Приближенное дифференциальное уравнение изогнутой срединной поверхности на основании зависимости (1.57)
.
Величина прогиба в середине мембраны получается на основании закона сохранения
энергии |
|
U = A. |
(1.59) |
31
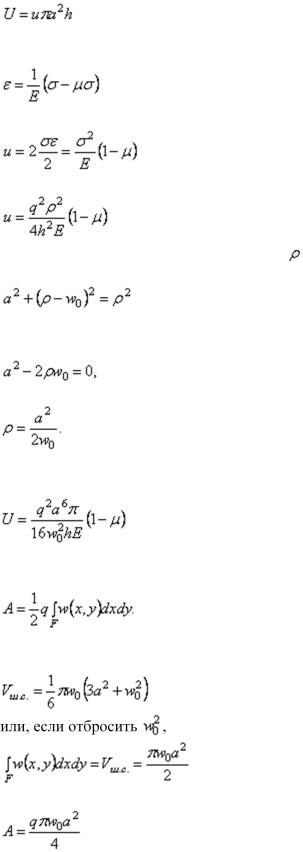
где U – потенциальная энергия деформации мембраны;
A – работа внешних сил на перемещениях, вызванных деформацией мембраны.
Потенциальная энергия мембраны |
|
, |
(1.60) |
где удельная потенциальная энергия деформации с учетом того, что на основании закона Гука
,
может быть выражена через напряжение следующим образом:
.
Тогда, на основании формулы, (1.58) |
|
. |
(1.61) |
Зависимость между радиусом кривизны |
и прогибом W0 в середине мембраны (рис. |
35,б) |
|
или после возведения скобки в квадрат и отбрасывания 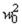 как величины высшего порядка малости
как величины высшего порядка малости
откуда
(1.62)
Подстановка этого значения 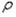 в формулу (1.61) и значения и в формулу (1.60) дает выражение для потенциальной энергии
в формулу (1.61) и значения и в формулу (1.60) дает выражение для потенциальной энергии
. |
(1.63) |
Работа А внешних |
сил получится как интеграл, взятый по площади мембраны, |
половины произведения элементарной силы qdxdy на прогиб w (ху):
(1.64)
Интеграл в выражении (1.64) представляет собой объем Vш.с. шарового сегмента с высотой W0 и радиусом а:
.
Поэтому выражение (1.64) примет вид
. |
(1.65) |
При подстановке значений (1.63) и (1.65) в выражение (1.59), получаем
32
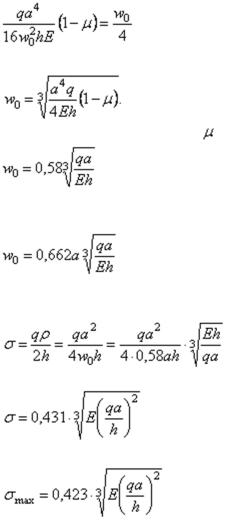
.
Тогда прогиб в середине мембраны
Для стальной мембраны при |
= 0,3 прогиб |
. |
(1.66) |
Точное решение, полученное путем интегрирования дифференциальных уравнений
(1.53), дает
.
Нормальное напряжение 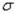 получается, если в формулу (1.58) подставить ρ из формулы (1.62) и w0 из формулы (1.66):
получается, если в формулу (1.58) подставить ρ из формулы (1.62) и w0 из формулы (1.66):
или
.
Точное решение на базе системы (1.53) дает выражение
.
33
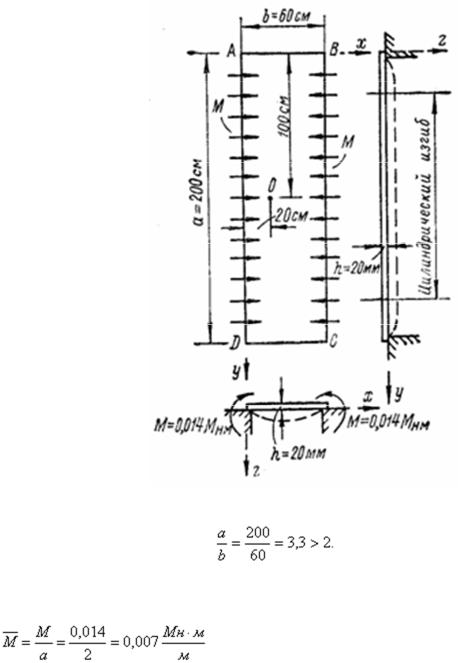
Пример выполнения задачи 1 из РГР «Расчет пластин и оболочек»
Задание
Определить нормальные напряжения 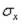 и
и 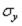 в точке на верхней поверхности
в точке на верхней поверхности
прямоугольной пластины, испытывающей изгиб от моментов М, распределенных по кромках AD и ВС. Определить радиус кривизны 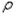 изогнутой срединной поверхности и наибольший прогиб w. Все значения взять из таблицы данных в соответствии с номеров варианта.
изогнутой срединной поверхности и наибольший прогиб w. Все значения взять из таблицы данных в соответствии с номеров варианта.
Решение
Отношение сторон пластины Следовательно, напряжения в средней части пролета можно вычислить по формулам цилиндрического изгиба.
Погонный изгибающий момент по кромкам AD и ВС
.
34

Напряжения:
Такие же напряжения будут во всех точках верхней поверхности в пределах цилиндрического изгиба.
Цилиндрическая жесткость:
Кривизна срединной поверхности:
поэтому дифференциальное уравнение изогнутой срединной поверхности
или
Два последовательных интегрирования дифференциального уравнения дают
Условия для определения произвольных постоянных: 1) х = 0, w = 0 (прогиб по кромке AD отсутствует); 2) х = 0,30 м, 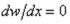 (касательная к изогнутой срединной поверхности в середине пролета горизонтальна). Из первого условия следует, что С2 = 0.
(касательная к изогнутой срединной поверхности в середине пролета горизонтальна). Из первого условия следует, что С2 = 0.
Из второго условия 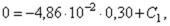 откуда
откуда
Подставляя найденные значения С1 и С2 в уравнение прогибов, получаем
Наибольший прогиб при х = 0,30 м
.
35
Раздел 2 . Теория расчета оболочек.
2.1 Общие сведения об оболочках
Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина h) мало по сравнению с другими размерами тела. Оболочки принадлежат к сплошным непрерывным системам (к дискретным системам относятся, например, стержневые системы). В настоящей главе рассматриваются наиболее часто применяемые в машиностроении оболочки постоянной толщины.
Оболочки широко применяются в различных отраслях техники. Например, подкрепленной замкнутой оболочкой является прочный корпус подводной лодки. Корпус парогенератора или турбины энергетической установки также рассчитывают как оболочку.
Цистерны, воздушные и газовые баллоны обычно представляют собой оболочки вращения цилиндрической, шаровой или каплевидной формы. Как оболочки рассматриваются и строительные конструкции − перекрытия и купола всевозможных очертаний со значительными пролетами, а также самолетные конструкции (фюзеляж, крылья и оперение).
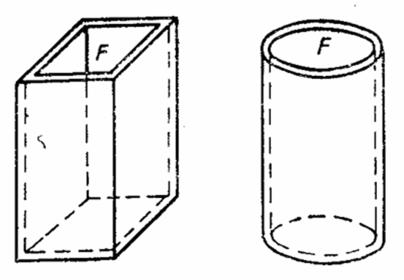
Большое распространение оболочек объясняется их экономичностью по сравнению с равнопрочными конструкциями, состоящими из плоских пластин. Например, при одной и той же площади F поперечного сечения сосуда и одинаковом постоянном внутреннем давлении наибольшие напряжения в стенке сосуда вдали от торцов при прямоугольной призматической форме (рис. 36,а) будут в несколько десятков раз больше, чем при цилиндрической форме (рис. 36, б). Это обусловлено тем, что в пластинах, образующих прямоугольный сосуд, вследствие изгиба наблюдается большая неравномерность распределения напряжении, чем в цилиндрической оболочке.
а |
б |
Рис. 36
36
Срединной поверхностью оболочки называется геометрическое место точек, равноудаленных от ее наружной и внутренней поверхностей. Считается, что кромка незамкнутой оболочки образована поверхностью, нормальной к срединной поверхности.
Условно, в зависимости от отношения толщины h оболочки к наименьшему радиусу R кривизны ее срединной поверхности, различают два класса оболочек: толстые оболочки, у
которых |
, и тонкие оболочки, у которых |
. В уравнениях, относящихся к |
|
тонкой оболочке, наибольшим значением |
можно пренебречь по сравнению с единицей, |
||
не превышая обычную для технических расчетов погрешность в 5 % :
Большая часть оболочек, применяемых в машиностроении, относится к тонким оболочкам, однако основана на использовании достаточно сложного математического аппарата. Их теория построена в предположении, что материал изотропен, обладает идеальной упругостью, подчиняется закону Гука и перемещения точек оболочки малы по сравнению с ее толщиной. Кроме того, используются два допущения теории пластин: 1) о прямых нормалях, т. е. считается, что линейные элементы оболочки, нормальные к срединной поверхности, остаются прямолинейными и нормальными к изогнутой срединной поверхности; 2) об отсутствии поперечного давления, т. е. предполагается, что нормальные напряжения, перпендикулярные к срединной поверхности, пренебрежимо малы.
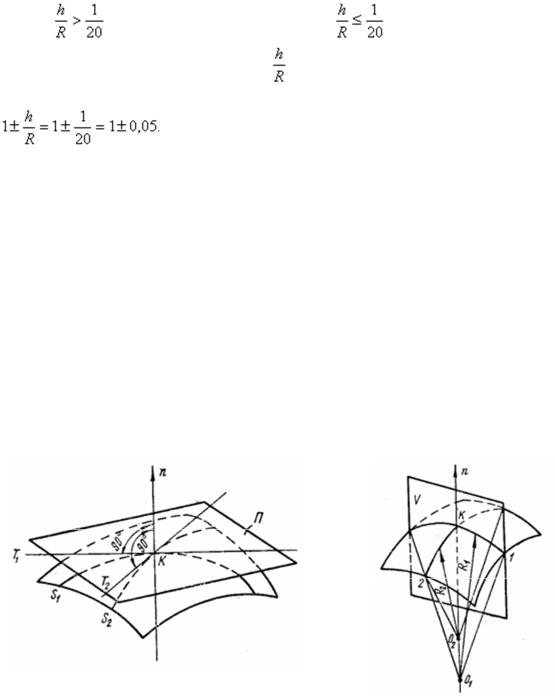
Напомним некоторые сведения из теории поверхностей. В любой точке К криволинейной поверхности (рис. 37,а) имеется плоскость П, касательная к поверхности, в которой лежат все касательные Т к плоским кривым S, проведенным на поверхности. Нормаль n в точке К перпендикулярна к касательной плоскости.
а |
б |
Рис. 37
Нормальное сечение поверхности в точке К получается, если рассечь ее плоскостью V, содержащей нормаль п (рис. 37,б). В любой точке К можно провести на поверхности две взаимно перпендикулярные линии главной кривизны, из которых одна имеет наибольший радиус кривизны R1, а другая наименьший R2 по отношению к радиусам всех линий, проходящих через точку К.
37
Величины 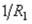 и
и 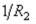 , обратные этим радиусам, называются главными кривизнами. Центры кривизны О1 и O2 в общем случае не совпадают.
, обратные этим радиусам, называются главными кривизнами. Центры кривизны О1 и O2 в общем случае не совпадают.
2.2 Понятие о расчете оболочки произвольной формы
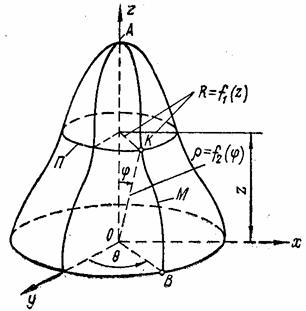
При изучении оболочек произвольной формы в общем случае пользуются системой криволинейных координат. Для оболочек вращения применяют цилиндрическую или сферическую системы.
При цилиндрической системе (рис. 38) за координаты принимаются: расстояние z по вертикали, отсчитываемое от точки О, определяющее параллель П, и угол 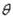 , отсчитываемый от начальной плоскости у0z, определяющий положение плоскости BOA, в которой лежит меридиан М. Пересечение параллели П и меридиана М определяет положение точки К на поверхности. Радиус R представляет собой функцию от z.
, отсчитываемый от начальной плоскости у0z, определяющий положение плоскости BOA, в которой лежит меридиан М. Пересечение параллели П и меридиана М определяет положение точки К на поверхности. Радиус R представляет собой функцию от z.
Рис. 38
При сферической системе за координаты принимаются: угол 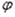 , отсчитываемый в плоскости BOA от вертикальной оси z, определяющий положение параллели П, и угол
, отсчитываемый в плоскости BOA от вертикальной оси z, определяющий положение параллели П, и угол 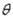 , определяющий положение меридиана М. Радиус
, определяющий положение меридиана М. Радиус 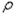 представляет собой функцию от
представляет собой функцию от 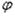 .
.
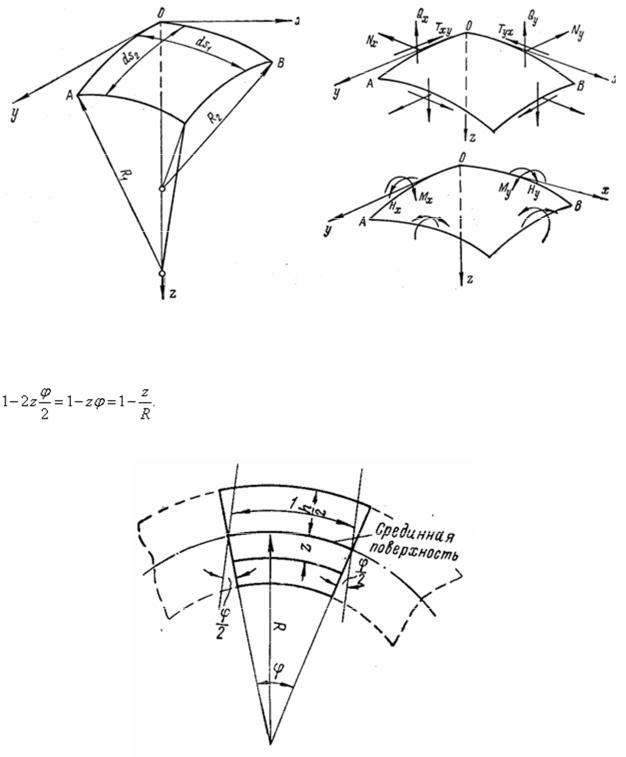
Выделим из оболочки, нагруженной непрерывно распределенной нагрузкой, элемент АОВ (рис. 39,а) двумя парами смежных взаимно ортогональных сечений, содержащих главные кривизны оболочки. Обозначим через R1 и R2 соответствующие радиусы главных кривизн. Взаимно перпендикулярные оси х и у направим по касательным в точке О к линиям главных кривизн, а ось z − по нормали к срединной поверхности в точке О. На элемент АОВ действуют десять погонных усилий (рис. 39,б): изгибающие моменты Мх и My, крутящие моменты Нх и Ну, продольные силы Nx и Ny, поперечные силы Qх и Qy и сдвигающие силы Тxу и Туx. Так как элемент выделяется взаимно ортогональными плоскостями, нормальными к срединной поверхности, в пересечении плоскостей с оболочкой образуются фигуры, имеющие разные длины волокон в зависимости от длины радиусов R1 и R2.
38
а |
б |
Рис. 39
Размер волокна длиной, равной единице (рис. 40), на расстоянии z от срединной поверхности с радиусом R после деформации окажется
Рис. 40
Поэтому для погонных усилий, действующих по граням выделенного элемента АОВ (рис. 39,б и 40), можно составить выражения:
39
