10953

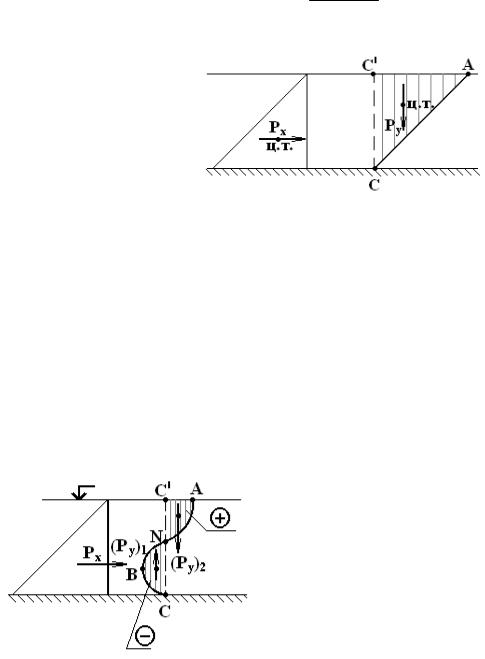
30

прямоугольника можно поступить аналогично рассмотренному случаю. Здесь следует отметить, что величина Р = 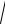РХ + РY равна значению силы по уравнению

(2.57).

Рис. 2.19 Эпюры составляющих силы давления на плоскую прямоугольную фигуру

2.9.3 Случай цилиндрической поверхности, когда имеются положительные и отрицательные тела давления

На рис. 2.20 представлена цилиндрическая поверхность АВС, которая пересекается в некоторой точке N с вертикалью СС', проведенной через нижнюю точку С цилиндрической поверхности. Как видно из рис. 2.20, одновременно получаются два тела давления с силами Рy1 и Py2, направленными в противоположные стороны. Складывая силы (Рy1) и (Py2) получаем результирующую силу Рy.

Рис. 2.20 Эпюра вертикального давления на цилиндрическую поверхность

АNВC

Рx = Рh

(Рy)1; (Рy)2

Поперечное сечение тела давления (отрицательного или положительного) представляет собой фигуру, заключенную между вертикалями из крайних точек до поверхности жидкости, и самой цилиндрическою поверхностью. Если рассматриваемая цилиндрическая поверхность со стороны тела давления не смачивается жидкостью, то имеем отрицательное тело давления (направление Рy вверх), в противном случае – положительное тело давления.

Заключительное замечание:

При решении задачи определения усилий от гидростатического давления на цилиндрические поверхности необходимо руководствоваться правилом: поперечное сечение тела давления (отрицательного или положительного) представляет собой

31

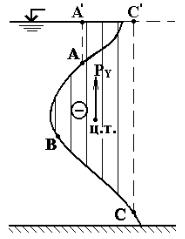
фигуру, заключенную между вертикалями, проведенными из крайних точек рассматриваемой цилиндрической поверхности до свободной поверхности воды.

Если рассматриваемая цилиндрическая поверхность со стороны тела давления не смачивается жидкостью, то имеем отрицательное тело давления (сила Рy направлена вверх), в противном случае – положительное тело давления (сила Рy – направлена вниз).

Рис. 2.21 Построение поперечного сечения тела давления для цилиндрической поверхности АВС, когда крайние точки А и С не лежат ни на свободной поверхности, ни на дне

На рис. 2.21 представлено тело давления в виде фигуры А'АВСС'

2.10 Круглая труба, подверженная внутреннему гидростатическому давлению

Рассмотрим давление на стенки трубы со стороны жидкости, находящейся внутри трубы (внутреннее гидростатическое давление) и давление на стенки изогнутой трубы

2.10.1 Внутреннее гидростатическое давление на стенки прямолинейной трубы

Представим на рис. 2.22 поперечное сечение горизонтальной трубы, заполненной покоящейся жидкостью. В центре трубы давление р. В верхней точке а

считают, что в трубе по всему поперечному сечению р = сonst.

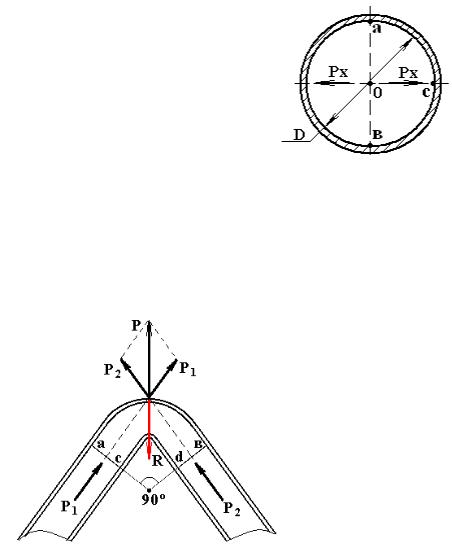
Под действием внутреннего давления р труба может разорваться, например, по плоскости ав. С тем, чтобы рассчитать толщину стенок е, необходимо знать силу РХ. Эта сила равна давлению на плоскую прямоугольную фигуру ав, являющуюся вертикальной проекцией цилиндрической поверхности асв.

32

Поскольку указанная прямоугольная фигура ав представляет собой

Сила РХ стремится разорвать трубу в двух местах у точек а и в, поэтому толщину стенки е следует рассчитывать на разрыв силой Рx/2.

Рис. 2.22 Внутреннее гидростатическое давление Рх, разрывающее трубу по линии ав

2.10.2 Сила гидростатического давления на стенки изогнутой трубы

Рис. 2.23 Сила гидростатического давления Р, действующего на колено изогнутой трубы

Колено трубы под действием гидростатического давления стремится сдвинуться в направлении силы Р. Эта сила представляет разность давлений:

а) на относительно бó льшую поверхность внутренней стороны трубы ав; б) на относительно малую поверхность внутренней стороны трубы сd.

Для отыскания силы Р выделим отсек жидкости авсd, находящийся в трубе. Данный отсек находится в покое под действием сил:

а также под действием реакции R стенок трубы в пределах колена: авсd.

R = P (2.74)

На величину силы Р рассчитываются анкерные опоры.

33

2.13 Простейшие гидравлические машины

Рис. 2.24 Гидравлический пресс

Рассмотрим простейшую гидравлическую машину – гидравлический пресс. К поршню П1, имеющему площадь S1 приложена сила Р1. Эта сила будет передаваться на жидкость, жидкость в свою очередь будет давить на поршень П2, имеющий площадь S2 с силой

S1

Как видно, при помощи пресса сила Р1 увеличивается в (S2/S1) раз. Здесь мы не учитываем силу трения в подвижных частях механизма.

2.12 Равновесие плавающих тел

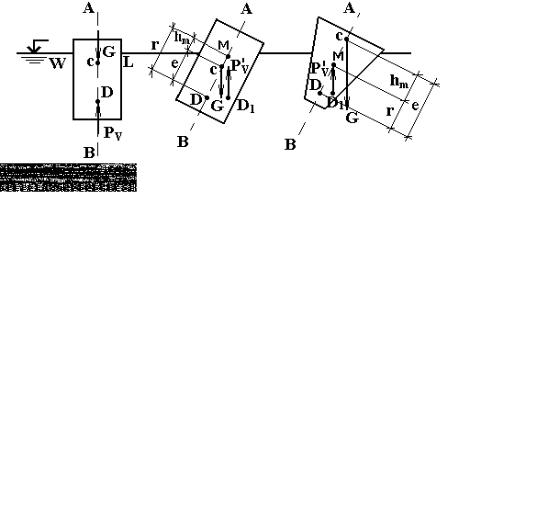
Рис. 2.25 Вертикальная подъемная сила РV, (архимедова сила); G – вес твердого тела; с – центр тяжести его; D – центр водоизмещения

Погрузим тело АВ в жидкость. Разобьем тело на ряд вертикальных столбиков. Рассмотрим один столбик. Сверху давит вес столба жидкости – ρ g h1 dS; снизу – вес столба жидкости, равный ρ g h2 dS. Рассматриваемый цилиндр площадью dS будет испытывать подъемное усилие, (направленное вверх):

Сумма элементарных подъемных сил dPV , действующих на все столбики, составляющих данное тело, даст нам полную подъемную силу РV, стремящуюся поднять тело вверх.

Вертикальная подъемная сила РV (Архимедова сила) равна весу жидкости в объеме рассматриваемого тела; точкой приложения силы РV является центр тяжести D объема жидкости. Точка D называется центром водоизмещения. В общем случае

34

точка D не совпадает с центром тяжести с твердого тела, где приложен его собственный вес G.

Различается 3 случая: PV < G – тело тонет;

PV > G – тело всплывает на поверхность;

PV = G – тело плавает в погруженном состоянии А) Случай PV = G

Здесь три варианта:

а) устойчивое равновесие; б) неустойчивое равновесие; в) безразличное равновесие.

а) б) в) Рис. 2.26 Плавание тела в погруженном состоянии

Б) Случай PV > G

Тело будет всплывать до тех пор, пока его часть не выйдет из жидкости, причем будет соблюдено условие

G = P′

V

PV′ – вес жидкости, вытесненной плавающим телом

Рис. 2.27 Плавание тела: а) состояние равновесия; б) остойчивое состояние; в) неостойчивое состояние

Рассмотрим схему, когда точка с (центр тяжести) выше точки D (центр водоизмещения). В этом случае можем получить как неустойчивое равновесие, так и устойчивое равновесие.

WL – площадь грузовой ватерлинии (площадь горизонтального сечения судна по линии WL)

АВ – ось плавания с – центр тяжести судна

35

D1 – центр водоизмещения при крене судна

М – точка пересечения оси плавания АВ с вертикалью, проведенной через центр водоизмещения D1, эта точка называется метацентром.

Сопоставляя два разных судна (схемы б, в), видим следующее:

1)на схеме (б) центр водоизмещения D1 при крене оказался правее точки с, причем возник момент, возвращающий судно в положение покоя. Данный случай характеризуется тем, что метацентр М лежит выше точки с.

2)на схеме (в) центр водоизмещения D1 при крене оказался левее точки с, причем возник момент, опрокидывающий судно. Данный случай характеризуется тем, что метацентр М лежит ниже точки с.

Dс = е – эксцентриситет;

сМ = hм – метацентрическая высота;

DM = r = е + hм – метацентрический радиус.

hм – считается положительной, если М расположена выше с; отрицательной – ниже. Остойчивостью судна называют способность его возвращаться в состояние

равновесия после получения крена.

1)hм > 0; r > е – судно остойчивое;

2)hм < 0; r < е – судно неостойчивое.

Чем больше r величины е, тем больше остойчивость судна. Следует отметить, что эксцентриситет е для данного плавающего судна не является постоянной величиной.

2.13Вывод дифференциальных уравнений покоя жидкости по Л.Эйлеру.

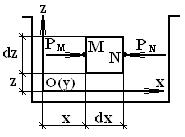
Вразделе 2.3 рассмотрено получение зависимости величины гидростатического давления от силы тяжести. В представленном разделе рассматривается также покоящаяся жидкость, на которую действует та или иная внешняя объемная сила (необязательно сила тяжести). Обозначим через F внешнюю объемную силу через, отнесенную у единице массы рассматриваемой жидкости. Проекции F на оси координат Ox, Oy, Oz соответственно будут Fx, Fy, Fz.

Рис. 2.28 Действие внешней силы F на выделенный элемент

В общем случае давление р в разных точках покоящейся жидкости будет

где ρ dx dy dz – масса жидкости, образующей рассматриваемый параллелепипед.

Сумма проекций всех сил на ось Ox составит:

Аналогично можно рассмотреть все подобно для осей Oy и Oz. Отсюда получим:

Как отмечалось ранее, эти уравнения были получены Л.Эйлером в 1755г. Далее выполним интегрирование указанных дифференциальных уравнений.

Для этого умножим первое дифференциальное уравнение на dx, второе – на dy и третье – на dz. После сложим левые и правые части:

Согласно (2.77) давление р в любой точке есть функция только координат, отсюда выражение, заключенное в скобки с величиной давления р, можно счиать полным дифференциалом давления р. Из этого следует:

2.14 Равновесие жидкости, находящейся в состоянии относительного покоя во вращающемся сосуде

Рассмотрим случай, когда на жидкость помимо объемных сил тяжести, действует дополнительная система объемных сил в виде центробежных сил инерции.

Возьмем круглоцилиндрический сосуд, заполненный жидкостью, который вращается равномерно вокруг своей вертикальной оси. Благодаря силам трения, стенки сосуда будут увлекать за собой жидкость, которая по истечении определенного времени также будет вращаться равномерно с угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Поэтому здесь для исследования вращающейся жидкости могут быть применены уравнения Л.Эйлера.

Будем рассматривать общую объемную силу Ф, включающую две составляющие: силу тяжести и силу инерции. Схема представлена на рис. 2.29. Внутри жидкости наметим точку m, около нее выделим элементарную массу dM, которая будет вращаться вокруг сосуда, двигаясь по дуге окружности радиуса r. Центробежная сила, действующая на данную массу равна:

где υ – средняя скорость движения массы dM по окружности радиуса r. Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной

в точке m:

Эта сила, так же как и сила I' направлена по радиусу от оси сосуда наружу. Проекции силы I на оси координат:

38

Проекции объемной силы тяжести, отнесенной к единице массы жидкости, в направлении осей x и y равны 0, а в направлении оси z из уравнения (2.11) Фz = -g (здесь ось z направлена вверх, в отличие от схемы рис. 2.5)

Складывая объемные силы тяжести и центробежные силы, отнесенные к единице массы, получаем:

Рис. 2.29 Цилиндрический сосуд, вращающийся относительно оси Oz. АОВ – свободная поверхность жидкости

После интегрирования (2.99) получаем:

Это последнее уравнение и выражает закон распределения давления в рассматриваемом сосуде. Пользуясь им, можно найти поверхности равного

39

давления. Действительно, уравнение поверхности, во всех точках которой давление рА = ре = const, запишется в виде

Уравнение (2.103) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью). Свободная поверхность жидкости, характеризующаяся постоянным давлением ре = ро, представляет собой также параболоид вращения; ее уравнение будет:

следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:

где zo – ордината кривой параболы АОВ.

Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину а, можно найти, пользуясь (2.102):

где h = a + zo.

Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью (2.17), пригодной для спокойного состояния воды.

2.15Задачи к практическим занятиям по гидростатике

1.Определить заглубление h точки под уровнем воды в водоеме, если избыточное гидростатическое давление в этой точке равно 80 кПа.

2.Определить абсолютное рА и избыточное р гидростатическое давление в точке дна открытого сосуда, наполненного водой, глубина воды в сосуде 300 см.

3.На рис. 2.30 представлена схема закрытого сосуда с обратным пьезометром.