Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

10855

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

14.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Последнее равенство справедливо по теореме о сложении вероятностей несовместных событий. Аналогично доказываются два других равенства.

3. Плотность распределения вероятностей непрерывной случайной величины

Определение. Плотностью распределения вероятностей (или со-

кращённо плотностью вероятности) ϕ(x) непрерывной случайной величины называется производная от её функции распределения F (x) , если только существует эта производная:

ϕ(x) = F '(x) .

_______________

Пример. Найти плотность вероятности случайной величины X (величины Релея), которая принимает неотрицательные значения, а её функция распределения равна F (x) = 1 − e− k 2 x 2 .

Решение. Т.к. F (x = 0) = 0 и F (x) не убывает (1 - e−k 2 x 2 > 0 при x < 0 ), то на самом деле:

	- e	−k	2 x	2
1	- e			при x ³ 0	.
F (x) =					.
				при x < 0
0				при x < 0

Поэтому:

- e

−k

2 x

при x ³ 0

− k 2 x 2

)(-k

× 2x)

при x ³ 0

)'x

- (e

ϕ(x) = F '(x) =

при x < 0

x e

−k 2 x 2

при x ³ 0

при x < 0

4. Свойства плотности вероятности

Свойство 1o . Вероятность того, что случайная величина X примет какое-либо значение x из замкнутого интервала [a,b] , равна

P(a £ X £ b) = ∫ j(x) dx .

Доказательство. Функция распределения F (x) - непрерывна, т.к. существует производная ϕ(x) = F '(x) . Поэтому по следствию из свойства 4o для непрерывной функции распределения:

P(a ≤ X ≤ b) = F (b) − F (a) ,

а по формуле Ньютона-Лейбница:

b	b
F (b) − F (a) = ∫ F '(x) dx = ∫ j(x) dx .
a	a

Поэтому P(a £ X £ b) = ∫ j(x) dx .

Что и требовалось доказать.

Пример. Плотность вероятности случайной величины X задана:

j(x) = 1 . p(1 + x 2 )

Найти вероятность того, что случайная величина X примет значение на интервале [0;5] .

Решение. По только что доказанному свойству:

5	5	1				1	5	dx			1			1
P(0 £ X £ 5) = ∫ j(x) dx =∫					dx =		∫			=		arctg x	05 =		( arctg 5 - 0) » 0,435 .

			2					2						p
0	0	p(1 + x		)		p	0	(1 + x	)		p			p

Свойство 2o . Функция j(x) , плотность распределения вероятностей , всегда неотрицательна, т.е.

j(x) ³ 0 .

Доказательство. Поскольку F (x2 ) ³ F (x1 ) при x2 > x1 (по свойству 3o для функции распределения), то:

j(x = x ) = F '(x = x ) = lim				F (x2 ) - F (x1 )	³ 0 ,

1	1	x2	→ x1	x2 - x1

как отношение двух неотрицательных величин. Что и требовалось доказать.

+∞

Свойство 3o . ∫ j(x) dx = 1.

−∞

Доказательство. По только что установленному свойству 2o ( j(x) ³ 0 ) плотности вероятности:

+∞ + A

∫ j(x) dx ³ ∫ j(x) dx

−∞ − A

при любом достаточно большом A . Но по свойству 1o для плотности вероятности:

∫j(x) dx = P(-A £ X £ A)

−A

при любом достаточно большом A . Следовательно:

+∞ + A

∫ j(x) dx ³ ∫ j(x) dx = P(-A £ X £ A) = F ( A) - F (-A)

−∞ − A

по следствию для непрерывной функции распределения. Откуда, переходя к пределу при A ® +¥ (неравенство сохранится), получаем:

+∞			(F ( A) - F (-A)) = lim F ( A) - lim F (-A) = F (+¥) - F (-¥) .
∫	j(x) dx ³ lim
		A→+∞	A→+∞	A→+∞
−∞

Откуда по свойству 2o для функции распределения:

+∞

∫ j(x) dx ³ F (+¥) - F (-¥) = 1 - 0 = 1.

−∞

Поскольку вероятность события не может быть больше 1, постольку

+∞

∫ ϕ(x) dx = 1.

−∞

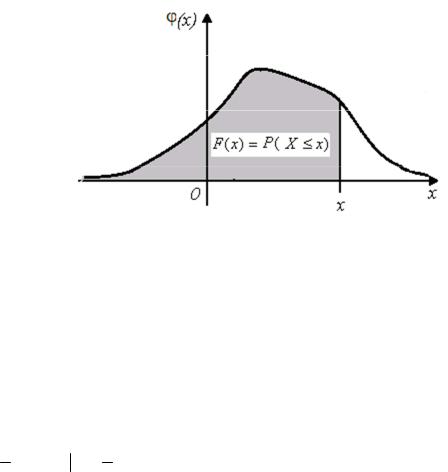
В силу доказанных сейчас свойств, функция ϕ(x) плотности распределения вероятностей всегда неотрицательна (по свойству 2o ). Она стремится к нулю при стремлении x → −∞ и x → +∞ (т.к. по свойству 3o площадь между графиком функции ϕ(x) и осью абсцисс равна единице). Примерный график функции ϕ(x) плотности распределения вероятностей изображён на следующем рис. 6.3.

Рис. 6.3. Иллюстрация свойств 1-3 функции плотности распределения

Свойство 4o . Функция распределения F (x) равна

F (x) = ∫ ϕ(t) dt .

−∞

Доказательство. Для несобственного интеграла

∫ ϕ(t) dt

−∞

справедливо:

x	ϕ(t) dt = lim		x	ϕ(t) dt ,
∫	ϕ(t) dt = lim			ϕ(t) dt ,
∫		A→−∞ ∫
−∞			A
а по свойству 1o для плотности распределения вероятностей:
x
∫ ϕ(t) dt = P( A ≤ X ≤ x) .
A
По следствию из свойства 4o	для непрерывной функции распределения:

∫ ϕ(t) dt = P( A ≤ X ≤ x) = F (x) − F ( A) .

Поэтому, переходя к пределу, получим:

x		x	ϕ(t) dt = lim	(F (x) − F ( A)) = F (x) − lim F ( A) = F (x) − F (−∞) .
∫	ϕ(t) dt = lim
		A→−∞ ∫	A→ −∞	A→ −∞
−∞		A
По свойству 2o		для функции распределения F (−∞) = 0 , т.е.

∫ ϕ(t) dt = F (x) − F(−∞) = F(x) .

−∞

Что и требовалось доказать.

Итак, для полной характеристики случайной величины достаточно знать или функцию распределения, или плотность распределения вероятностей (т.к. одну из них можно выразить через другую):

F (x) = ∫ ϕ(t) dt или ϕ(x) = F '(x) .

−∞

Рис. 6.4. Иллюстрация свойства 4 функции плотности распределения

______________

Пример. Найти функцию распределения случайной величины, плотность вероятности которой:

ϕ(x) =	1	.
	π(1 + x 2 )

Решение. По только что доказанному свойству:

F (x) = ∫ ϕ(t)

−∞

= π1 arctg t −∞x = π1 ( arctg x − arctg

dt = ∫

dt =

π(1 + t

)

−∞

( arctg x + π ) =

(−∞) )

arctg x .

Лекция № 7

Примеры распределения непрерывных случайных величин

1. Равномерное распределение

Определение. Случайная величина с плотностью вероятности

0	при x < a и x > b	где C = const,
ϕ(x) =	,	где C = const,
C	при a < x < b

называется равномерно распределённой величиной.

Равномерный закон распределения используется: при анализе ошибок измерения, когда проводятся численные расчёты; в ряде задач массового обслуживания.

+∞

Найдём величину C из условия ∫ ϕ(x) dx = 1

(свойство 3o плотности ве-

роятности):

−∞

+∞

∫

j(x) dx =

∫

0 × dx +

∫

C × dx +

∫

0 × dx = C

∫

dx = C x

b = C(b - a) = 1.

должно

−∞

быть

Поэтому С =

, а плотность вероятности равномерно распределённой ве-

b - a

личины имеет вид:

при x < a

x > b

j(x) =

при a < x < b

- a

Найдём также функцию распределения равномерно распределённой

величины. По свойству 4o

для плотности вероятности:

при x < a

∫ 0 × dt

−∞

F (x) = ∫ j(t) dt = ∫ 0

× dt

+ ∫

при a < x < b

b - a

−∞

∫ 0 × dt + ∫

dt + ∫ 0 × dt

при b < x

b - a

−∞

при x < a

x - a

= ∫

при a < x < b =

(x - a)

при a < x < b =

при a < x < b .

b - a

- a

b - a

при b < x

(b - a)

при b < x

∫

при b < x

- a

b - a

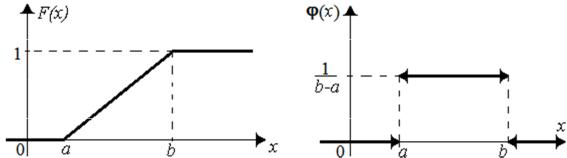
Графики функций F (x) и j(x)

приведены ниже на рис. 7.1. На графике

для функции j(x) четыре стрелки означают,

что левый или правый пределы

не достижимы функцией в соответствующей точке.

Рис. 7.1. Равномерное распределение

Пример. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придётся не более полминуты.

Решение. Пусть случайная величина X - время ожидания пассажира. Тогда её плотность вероятности равна:

0		при x < 0 и x > 2
		.
ϕ(x) = 1
		при 0 < x < 2

2

Поэтому по свойству 1o для плотности вероятности получим:

	1	2	1		1	2	1		1 / 2
P(0 ≤ X ≤		) = ∫		dx =		∫ dx =		x
	2		2		2		2		0

		0				0

=1 .

2. Нормальное распределение

Определение. Случайная величина имеет нормальный закон распреде-

ления (закон Гаусса), если её плотность распределения вероятностей имеет вид:

ϕ(x) =	1	− ( x−a )2
			2σ2	,

	2π σ e
	2π σ e

где a и σ - параметры распределения ( σ > 0, − ∞ < a < +∞ ).

Нормальный закон распределения наиболее часто встречается на практике. Главная его особенность – он является предельным законом, к которому приближаются другие законы распределения (при типичных условиях).

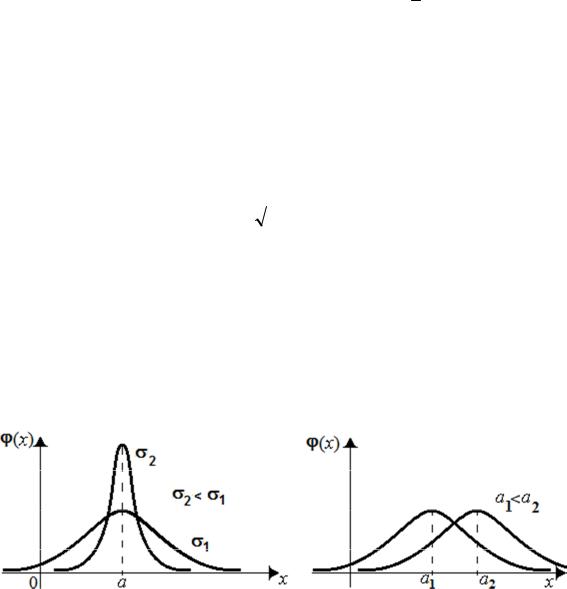
Плотность вероятности ϕ(x) - функция, похожая на колокол. Зависимость от параметров такова (рис. 7.2). При уменьшении только параметра σ , график функции вытягивается и поднимается вверх по оси ординат. А при увеличении только параметра a , график симметрично передвигается вправо вдоль оси абсцисс:

Рис. 7.2. Функция плотности распределения нормальной величины

Функция распределения F (x) нормального распределения

x	1	x	−	(t −a )2
F (x) = ∫ ϕ(t) dt =	1	∫ e		2 σ2	dt
F (x) = ∫ ϕ(t) dt =		∫ e			dt
−∞	2π σ −∞

имеет вид, изображенный на рис. 7.3:

Рис. 7.3. Функция распределения нормальной величины

а) Правило «трёх сигм»

Найдём вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от α до β :

β	1	β	−	( x−a)2
P(α ≤ X ≤ β) = ∫ ϕ(x) dx =		∫ e		2 σ2
					dx .

α	2π σ α

Для этого воспользуемся известным из математического анализа свойством определённого интеграла:

b c b

∫ f (x) dx = ∫ f (x) dx +∫ f (x) dx

a	a	c
и, используя ещё одно свойство:
	c	a
	∫ f (x) dx = −∫ f (x) dx ,
	a	c
окончательно получим:
b	b	a
∫ f (x) dx = ∫ f (x) dx −∫ f (x) dx .
a	c	c

Этим равенством и воспользуемся (при условии, что роль c играет параметр a из нормального закона)

β −

( x−a)2

−

( x−a)2

−

( x−a)2

P(α ≤ X ≤ β) =

∫ e

2 σ2

∫ e

2 σ2

−

∫ e

2 σ2

dx .

2π σ

2π σ a

Далее сделаем замену t =

x − a

в определённых интегралах (тогда dt = d (

x − a

)

или dx = σ dt ):

− ( x−a)2

P(α ≤ X ≤ β) =

σ2

−

2 σ2

2π σ

2π σ ∫a

∫a

β−a

α − a

−

t 2

−

t 2

∫

σ dt

−

∫

σ dt =

e 2

2π σ a−a

2π σ a −a

β−a

α−a

−

t 2

−

t 2

β − a ) − Φ( α − a ) ,

∫ e

dt −

∫ e

dt = Φ(

2π

−

z 2

где функция Лапласа

Φ(x) =

∫ e

затабулирована и приводится в при-

2 dz

2π

ложении 2 из [2]. В частном случае, когда интервал симметричен относительно точкиa , эта формула выглядит так:

P(a − ε ≤ X ≤ a + ε) = F( a + ε − a ) s

или так:

P( X − a

- F( a − ε − a ) = F( ε ) s s

≤ ε) = 2 F( sε ) .

- F( −sε ) = 2 F( sε )

Отсюда правило «трёх сигм» выводится следующим образом. Рассмотрим вероятность того, что изучаемая случайная величина (распределённая нормально) примет значение в пределах от a - 3s до a + 3s :

P(a - 3s £ X £ a + 3s) = 2 F(3s / s) = 2 F(3) .

Из таблицы для функции Лапласа находим, что F(x) = 0,49865, поэтому

P(a - 3s £ X £ a + 3s) = 2 × 0,49865 » 0,9973 ,

т.е. вероятность встретить значение изучаемой случайной величины именно на интервале [a - 3s, a + 3s] велика - 0,9973 !!!

3. Показательный (экспоненциальный) закон распределения

Определение. Случайная величина X имеет показательный (экспо-

ненциальный) закон распределения, если её плотность распределения вероятностей имеет вид:

0		при x < 0
j(x) =	−λ x	,
l e	−λ x	при x ³ 0

где l - параметр распределения ( l > 0 ).
Он возникает в теории массового обслуживания, теории надёжности.

Например, интервал времени T между двумя соседними событиями (заявками) в потоке поступающих заявок на обслуживание (ремонт телевизоров, автомобилей, …) имеет показательный закон распределения (с интенсивностью l ).

Примерный график плотности распределения вероятностей j(x) приводится на рис. 7.4.

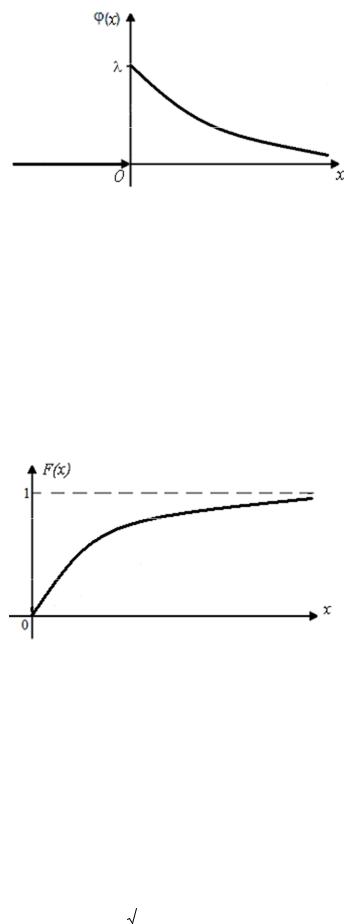
Рис. 7.4. Функция плотности распределения показательной величины

Определим вид функции распределения для показательного закона:

F (x) = ∫ ϕ(t) dt

−∞

x				при x < 0
	∫ 0 × d t =0			при x < 0
= −∞			0	x			x
	x		0	x			x
	∫ l e−λ t d t = ∫ 0 × d t + ∫ l e−λ t d t = - ∫
−∞			−∞	0			0
0		при x < 0			0		при
					0		при
=	- e−λ t	x	при x ³ 0		=		−λ x
=					=
					1	-e
		0			1	-e

e−λ t d (-lt)

при x ³ 0

x < 0

при x ³ 0

Примерный график функции распределения F (x) приводится на рис.7.5.

Рис. 7.5. Функция распределения показательной величины

4. Логарифмически-нормальное распределение

Определение. Случайная величина X ( X > 0) имеет логарифмическинормальное (логнормальное) распределение, если её натуральный логарифм ln X подчинён нормальному закону:

0			при	x < 0
			ln x		(t −a)2
F (x) = P(ln X < ln x) =	1			−
F (x) = P(ln X < ln x) =	1		e	−	2σ	2	d t	при x ³ 0 .


s		2p	∫0
			48

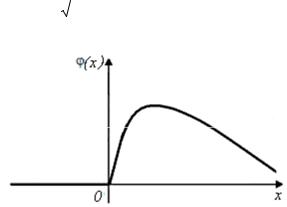
Отсюда, функция j(x) плотность распределения вероятностей логнормального распределения имеет вид (по правилу дифференцирования интеграла, зависящего от параметра)

0		при		x < 0
				(ln x−a)2
j(x) =	1		−
				2σ	2	при x ³ 0 .
			e

s	2p x

Примерный вид графика функции j(x) приведён на рис. 7.6.

Рис. 7.6. Функция плотности распределения логнормальной величины

Логнормальное распределение встречается при описании распределения доходов, банковских вкладов, долговечности изделий в режиме износа – старения, месячной зарплаты, посевных площадей под различные культуры и т.п.

5.Вейбуловское распределение

Винженерной практике часто используется распределение ВейбуллаГнеденко:

0		при x < 0

F (х) =		−( x / α)	β
	-e	−( x / α)	при x ³ 0
1	-e		при x ³ 0

	0	при x < 0
,
,	j(x) =	β−1		−( x / α)	β
		β−1	e	−( x / α)		при x ³ 0
	(b/ a)(x / a)		e			при x ³ 0

с параметрами a > 0 и b > 0 . Данное распределение часто используется для описания распределения экстремальных значений системы случайных величин:

X max (n) = max(X1, X 2 ,...X n ) , X min (n) = min(X1, X 2 ,...X n ) ,

кроме того оно используется для описания времени и интенсивности отказов в теории надежности сложных систем.

Частными случаями распределения Вейбулла-Гнеденко являются следующие распределения :

-Показательное распределение a = 1/ l > 0 , b =1,

-Релеевское распределение a > 0 , b = 2 .

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.202314.46 Mб010850.pdf
#
25.11.202314.46 Mб010851.pdf
#
25.11.202314.46 Mб010852.pdf
#
25.11.202314.46 Mб010853.pdf
#
25.11.202314.46 Mб110854.pdf
#
25.11.202314.46 Mб010855.pdf
#
25.11.202314.46 Mб110856.pdf
#
25.11.202314.48 Mб210857.pdf
#
25.11.202314.49 Mб210858.pdf
#
25.11.202314.51 Mб010859.pdf
#
21.11.2023175.87 Кб01086.pdf