
10622
.pdf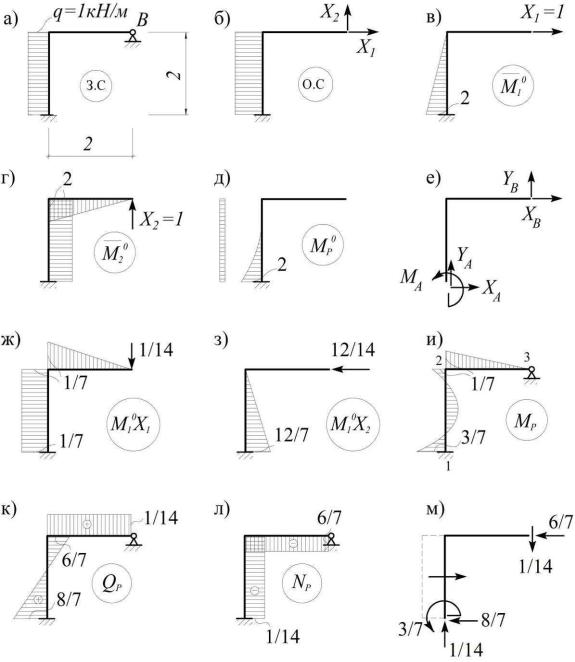
|
|
|
|
- 211 - |
|
|
|
|
|
|
M = M 0 |
+ Σ`M |
0X ; |
|
|
||
|
|
|
p |
p |
i i |
|
|
|
|
|
Q = Q 0 |
+ Σ`Q 0X ; |
|
(4.7) |
|||
|
|
p |
p |
i |
i |
|
|
|
|
|
N |
p |
= N 0 |
+ Σ`N |
0X , |
|
|
|
|
|
p |
i |
i |
|
|
|
где Mp, Qp, Np – |
соответствующие усилия в заданной СНС от заданной нагруз- |
|||||||
ки; M 0, Q |
0, N 0– |
те же усилия в ОС МС от заданной нагрузки; `M |
0, `Q |
0, `N 0 – |
||||
p p |
p |
|
|
|
|
i |
i |
i |
эти же усилия в ОС МС от Xi = 1.
Рис. 4.5
- 212 -
Поскольку при расчете рам учитываются только изгибные деформации, которым соответствуют изгибающие моменты, по формулам (4.7) определяют
лишь первое из внутренних усилий – Mp. Эпюру Qp удобнее построить по эпюре Mp, используя дифференциальную зависимость Qp = dMp/dx, а эпюру Np – по
эпюре Qp, рассматривая равновесие вырезанных узлов рамы.
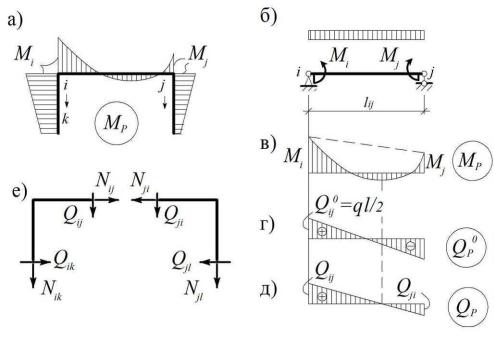
Рассмотрим такую процедуру на примере фрагмента рамы, приведенного на рис. 4.6, а.
Пусть на вертикально расположенных участках k-i и j-l эпюра Mp линейна и знакопостоянна, а на горизонтальном участке i-j, загруженном равномерно распределенной нагрузкой, представляет собой параболу.
Очевидно, что на последнем участке рамы эпюра Mp не отличается от эпюры моментов в простой двухопорной балке соответствующего пролета, загруженной равномерно распределенной нагрузкой и концевыми моментами (рис. 4.6, б), и ее в общем случае можно представить в виде суммы:
Mp (x) = Mp0 (x) + Mpк(x), |
(4.8) |
где Mp0 (x) – эпюра от собственной нагрузки внутри пролета, а Mpк(x) – эпюра от концевых моментов, показанная пунктиром на рис. 4.6, в.
l
Рис. 4.6
Дифференцируя (4.8), и рассматривая полученное выражение на концах участка, получим:
Qij = Qij0 + (M пр – M лев)/lij, |
(4.9) |
- 213 -
где Qij и Qij0 – поперечные силы от заданной и от местной нагрузки в i-м узле рамы на участке i-j (рис. 4.6, г– д), а М пр и М лев – значения моментов на концах
соответствующей балки, взятые с учетом знаков из сопромата. Аналогично под Qji будем понимать поперечную силу в j-ом узле этого участка. Тогда в нашем примере М пр = – Mj, а М лев = – Mi, поэтому
Qij = ql/2 + (Mi – Mj)/lij;
Qji = – ql/2 + (Mi – Mj)/lij.
Применяя соответствующие обозначения для продольных сил и рассматривая равновесие i-го узла рамы, получим (рис. 4.6, е):
SX = 0; Nij = – Qik;
SY = 0; Nik = – Qij.
Аналогичные уравнения, получаемые из условия равновесия рассматриваемого j-го узла рамы или ригеля i-j в целом, можно использовать для проверки найденных результатов.
Вернемся теперь к рассмотрению рамы на рис. 4.5, а.
Пример 4.3. Построить эпюры внутренних усилий для заданной рамы
(рис. 4.5, а).
Решение.
1. Находим изгибающие моменты по формуле (4.7):
Mp = Mp0 +`M10X1 +`M20X2,
воспользовавшись найденными ранее значениями X1 и X2 – см. пример 4.2.
На ригеле эта эпюра совпадает с эпюрой`M10X1 (рис. 4.5, ж), поскольку на этом участке эпюры Mp0 и`M20 равны нулю. Для построения Mp на стойке достаточно вычислить ее значения в 1-м узле (рис. 4.5, и): M1 = 2 + (1/7) – (12/7)
=3/7кНм.
2.При построении эпюры на стойке будем для определенности считать первый узел – левым, а второй – правым. Тогда по формуле (4.9) получим:
Q12 |
= ql12/2 + (M пр – M лев)/l12 = (1×2)/2 + [(–1/7) – (–3/7) ]/2 = 1 + 1/7 = 8/7; |
Q21 |
= - ql12/2 + (M пр – M лев)/l12 = - 1 + 1/7 = - 6/7кН. |
На ригеле местная нагрузка отсутствует, поэтому (рис. 4.5, к):
Q23 = Q32 = (1/7)/2 = 1/14кН.
3. Для построения эпюры Np достаточно рассмотреть равновесие 2-го узла рамы:
SX = 0; N23 = – Q21 = – 6/7 кН;
SY = 0; N21 = – Q23 = – 1/14 кН.
- 214 -
Для проверки правильности построения эпюр можно рассмотреть равновесие части рамы (рис. 4.5, м), расположенной выше сечения, проведенного вблизи опор A и B, где известны значения всех трех эпюр:
SX = 2 – 6/7 – 8/7 = 0;
SY = 2/7 – 2/7 = 0;
SMA= 3/7 – 2 ×1 + (6/7)×2 – (1/14) ×2 = 0. ·
4.4. Проверка правильности решения
При расчете статически неопределимых балок и рам эпюра Mp имеет решающее значение. Чтобы убедиться, что реакции лишних связей X1, X2, …, Xn найдены без ошибок и эпюра Mp построена правильно, выполняют кинемати-
ческую проверку.
На втором этапе расчета – при построении эпюр Qp и Np – выполняют статическую проверку правильности построения этих эпюр.
Кинематическая проверка. Для проверки эпюры Mp ее надо умножить на каждую из эпюр от единичных значений неизвестных – `Mi0. Результат должен быть равен нулю. Эта проверка имеет наглядный геометрический смысл и означает, что мы определяем перемещение Dip точки приложения Xi в направлении Xi от заданной нагрузки, которое, как это следует из сути метода сил, должно равняться нулю. В самом деле, учитывая, что формулу (4.7), сменив индекс суммирования i на j, можно записать в виде:
Mp = Mp0 + Sj`Mj0Xj, |
(4.7¢) |
и принимая во внимание формулы (4.4) – (4.6), получим:
Dip = Sk∫(Mp`Mi0/EJ)ds = Sk∫[( Mp0 + Sj`Mj0Xj)× (`Mi0 /EJ) ]ds =
= Sk∫(Mp0×`Mi0/EJ)ds + Sj[Sk∫ (`Mi0×`Mj0 /EJ)ds] Xj =Dip0 +Sjdij Xj = 0.
Статическая проверка. Позволяет проверить правильность построения эпюр Qp и Np по эпюре Mp и принципиально не отличается от такой же проверки эпюр, построенных для СОС. При этом рассматривается равновесие части рамы, расположенной по одну сторону от сечения, проведенного через точки, где известны значения всех трех эпюр – Mp , Qp и Np. Соответствующая процедура для СНС уже была рассмотрена в примере 4.3.
Пример 4.4. Выполнить кинематическую проверку правильности построения эпюры Mp для рамы на рис. 4.5, а в примере 4.3.
- 215 -
Решение. Умножая эпюру Mp (рис. 4.5, и) на единичные эпюры`M10 и`M20 (рис. 4.5, в, г) по правилу Верещагина, получим:
D1p = (Mp ´`M10) = (1/EJ)[(1/2)×2×(1/7)×(1/3)×2+(1/2)×2×(3/7)×(2/8)×1 –
– |
(2/3) ×2×1] = 0; |
D2p = (Mp ´`M20) = (1/EJ)[ – (1/2) |
×2×(1/7) ×2 – (1/2) ×2×(3/7)× 2 + |
+ (2/3)×2×(1/2)×2 – (1/2) ×2×(1/7)×(2/3)×2 = 0. |
|
Таким образом, кинематическая проверка выполняется. · |
|
Переходить к построению эпюр Qp и Np по эпюре Mp целесообразно лишь после того, как выполнена кинематическая проверка и есть уверенность, что эпюра Mp построена правильно.
Если ошибку найти не удается, можно попробовать решить задачу, выбрав другую основную систему.
Окончательно можно быть уверенным в правильности решения задачи лишь при одновременном выполнении кинематической и статической проверок. Отметим, что при этом возможны следующие варианты.
1. Кинематическая проверка выполняется, а статическая – нет. Скорее всего, это свидетельствует о правильности построения эпюры Mp и ошибке при построении эпюр Qp или Np.
Гораздо реже, но встречается ситуация, когда эпюра Mp соответствует не заданной, а какой-либо другой возможной нагрузке.
2. Кинематическая проверка не выполняется, а статическая – выполняется. Это возможно в случае, если правильно построены эпюры `Mi0 и Mp0, но неверно найдены реакции лишних связей Xi. Ошибка возможна при вычислении коэффициентов, свободных членов системы канонических уравнений, ее решении или при построении эпюры Mp по формуле (4.7).
В студенческих работах нельзя исключать и варианта, когда все эпюры построены правильно, а ошибка – в самой кинематической проверке.
3. Не выполняются как кинематическая, так и статическая проверки. Ошибка может быть допущена уже на стадии построения эпюр`Mi0 и Mp0 либо при построении эпюры Mp по формуле (4.7). При этом в последнем случае реакции Xi могут быть найдены правильно.
Примечания
1. В кинематической проверке речь идет о вычислении перемещения ip в системе, полученной из заданной СНС удалением, по крайней мере, одной i-ой связи и заменой ее соответствующей реакцией Xi .
2. Эпюру `Mi0 для кинематической проверки можно взять в ОС, отличной от той, которая применялась при построении эпюры Mp.
В системах с одной лишней связью все эпюры`M10, независимо от выбора ОС, с точностью до множителя будут равны.
-216 -
3.Очевидно, что если для рамы с двумя лишними связями D1p = 0, а D2p ¹ 0, то, скорее
всего, неправильно найдено значение X2, поэтому ошибку следует искать в вычислении D2p0 или d22.
4.Вместо того, чтобы умножать эпюру Mp на каждую из единичных эпюр`Mi0 , ее
можно умножить на их сумму`Ms0 = Si`Mi0, однако в этом случае будет труднее локализовать ошибку, если окажется, что Dsp = (Mp ´`Ms0) ¹ 0.
4.5. О выборе ОС МС. Признаки ортогональности эпюр
Напомним, что ОС МС получается из заданной СНС удалением лишних связей и их заменой неизвестными реакциями. Выясним, насколько мы свободны в выборе ОС, и как оценить качество нашего выбора.
Отметим, прежде всего, следующие моменты.
1.ОС выбирается не единственным способом, и более того, ее можно вы-
брать бесчисленным множеством способов. Так, для рамы на рис. 4.4, а в каче-
стве ОС помимо уже рассмотренной на рис. 4.4, б могут быть выбраны системы, приведенные на рис. 4.4, в– д.
2.Главным и безусловным требованием, предъявляемым к ОС, является требование ее неподвижности, то есть в качестве ОС нельзя выбрать геомет-
рически изменяемую систему (рис. 4.4, е) или мгновенно изменяемые системы
(рис. 4.4, ж, з).
3.Надо стремиться к выбору рациональной основной системы, чтобы соответствующая ей система канонических уравнений:
δ11 X1 + δ12 X2 + δ13 X3 + δ21 X1 + δ22 X2 + δ23 X3 + δ31 X1 + δ32 X2 + δ33 X3 +
0
1p
0
2p
0
3p
= 0 ; |
(4.3′) |
= 0 ; |
|
= 0 , |
|
имела как можно более простую структуру.
Для рамы на рис. 4.4, а такой будет ОС, приведенная на рис. 4.4, в. Нетрудно убедиться, что для нее δ12 = δ21 = 0, δ23 = δ32 = 0 и система трех линейных алгебраических уравнений (4.3) распадается на систему двух уравнений для определения X1 и X3 и одно независимое от них уравнение для определения X2:
δ |
X + δ |
13 |
X |
3 |
+ |
0 |
= 0; |
|
11 |
1 |
|
|
|
1p |
|
||
δ22 |
X2 |
+ |
2p0 |
= 0; |
|
|
||
δ |
X + δ |
33 |
X |
3 |
+ |
0 |
= 0. |
|
31 |
1 |
|
|
|
3p |
|
||
Чтобы выяснить, почему данная ОС оказалась удобнее остальных и почему для нее δ12 = δ23 = 0 , введем понятие ортогональности функций или ор-
тогональности эпюр.
Термин «ортогональность» является обобщением понятия «перпендикулярность» и в отношении двух векторов a и b из трехмерного пространства означает, что скалярное произведение этих векторов равно нулю:
- 217 -
i =3
(a×b) = ½a½×½ b½ cos (a,b) = axbx + ayby + azbz = ∑aibi = 0.
i =1
Аналогично, ортогональность двух векторов a и b из n-мерного пространства означает равенство нулю суммы произведений их одноименных компонент:
i=n |
|
(a×b) = ∑ aibi = 0. |
(4.8) |
i=1
Определение. Две функции f(x) и g(x) ортогональны на промежутке [0,l], если выполняется соотношение:
l |
|
∫ f(x) × g(x) dx = 0. |
(4.9) |
0 |
|
Классическим примером функций, ортогональных на промежутке [0,p], являются функции sin x и cos x .
Понятие ортогональности функций является естественным обобщением ортогональности векторов в n-мерном пространстве.
В самом деле, разбивая промежуток [0,l] на n частей длиной Dx = l/n узло-
выми точками xi = i(Dx), где i = 0,1, … , ( |
n – 1) и, переходя в (4.9) к численному |
|
интегрированию, получим: |
|
|
l |
|
n −1 |
∫ f(x) × g(x) dx = |
lim |
∑ f (xi) g (xi) Dx. |
0 |
x→0 |
i =0 |
Полагая в (4.8) ai = f (xi), bi = g (xi) Dx и переходя к пределу при Dx ® 0, а n ® ¥, мы и придем к (4.9).
Наконец, подставляя в (4.9) f(x) = `Mi0 и g(x) = `Mj0/EJ или g(x) =`Mp0/EJ и обобщая на случай n участков рамы, мы получим условие ортогональности этих эпюр в виде:
dij = (`Mi0 ´`Mj0) = S∫ (`Mi0×`Mj0 /EJ)ds = 0, |
(4.10) |
Dip0= (`Mi0 ´ Mp0)= S∫ (`Mi0× Mp0/EJ)ds = 0. |
(4.11) |
Из последних выражений можно получить признаки ортогональности
эпюр.
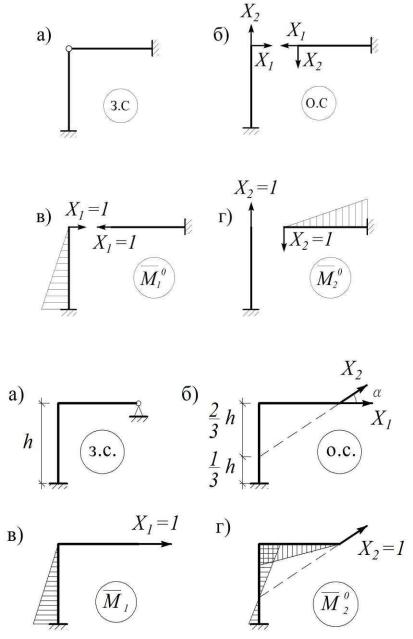
1. Две эпюры с взаимно нулевыми участками ортогональны. Примером служат эпюры `M10 и`M20 на рис. 4.7, в, и 4.7, г, соответствующие выбранной на рис. 4.7, б основной системе, для которой d12 = 0.
-218 -
2.Две эпюры ортогональны, если центр тяжести нелинейной эпюры лежит против нулевой точки линейной.
В качестве примера вернемся к раме на рис. 4.5, а − (рис. 4.8, а). Выберем вместо прежней ОС, показанной на рис. 4.5, б, новую ОС, в которой реакция X2 не перпендикулярна к X1, а направлена к ней под углом α (рис. 4.8, б). На стойке рамы центр тяжести эпюры`M10 (рис. 4.8, в) расположен против точки, где ордината эпюры`M20 равна нулю (рис. 4.8, г), поэтому по правилу Верещагина на этом участке их произведение равно нулю. На ригеле наоборот – эпюре`M20 соответствует нулевой участок эпюры`M10, поэтому в целом для выбранной основной системы δ12 = 0.
Рис. 4.7
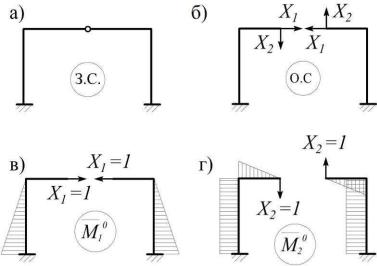
Рис. 4.8
-219 -
3)Симметричная и обратносимметричная эпюры ортогональны. Для рамы на рис. 4.9, а при симметричной ОС (рис. 4.9, б) эпюра `M10 симметрична,
а`M20 – обратносимметрична (рис. 4.9, г). При этом на левой половине рамы произведение эпюр`M10 и`M20 положительно, а на правой – равно по модулю тому же значению, но отрицательно, откуда и следует, что δ12 = 0.
Аналогично у рамы на рис. 4.4, а для ОС на рис. 4.4, в будут симметрич-
ными`M10 и`M30, а обратносимметричной – `M20, поэтому δ12 = δ23 = 0.
Рис. 4.9
Примечания
1.Напомним, что обратносимметричная (в литературе также встречается термин кососимметричная) эпюра получается из симметричной, если сменить на противоположный знак для части эпюры, расположенной по одну сторону от оси симметрии.
Очевидно, что понятия «симметричная» и «обратносимметричная» эпюры являются обобщением понятий четной и нечетной функций в математике. Для первых f (x) = f (– x), для вторых f (x) = – f (– x).
2.О симметричных и обратносимметричных эпюрах можно говорить лишь в отношении систем, обладающих свойством симметрии. При этом симметричными должны быть не только геометрические очертания, но и жесткости элементов конструкции.
3.Для системы с одной лишней связью вопрос о рациональном выборе основной системы, с учетом примечания 2 из предыдущего параграфа, целиком определяется видом эпю-
ры Mp0.
4.6. Расчет симметричных систем
При расчете симметричных систем можно упростить структуру системы канонических уравнений за счет обращения в ноль как коэффициентов δij, так и
свободных членов ip0.
В первом случае соответствующий прием носит название группировки неизвестных, во втором – результат достигается с помощью разложения нагрузки на симметричную и обратносимметричную.
- 220 -
Группировка неизвестных применяется для рам, у которых реакции лишних связей представлены только симметричными неизвестными. Примером служит рама на рис. 4.10, а для выбранной на рис. 4.10, б основной системы, где в канонических уравнениях
d11 X1 + d12 X2 + D1p0 = 0;
d21 X1 + d22 X2 + D2p0 = 0
все коэффициенты отличны от нуля. |
|
Чтобы упростить эту систему, перейдем от неизвестных X1 и X2 |
к новым |
неизвестным X1¢ и X2¢ по формулам: |
|
X1¢ = (X1 + X2)/2; |
(4.12) |
X2¢ = (X1 - X2)/2 |
|
где обратное преобразование: |
|
X1 = X1¢+ X2¢; |
(4.13) |
X2 = X1¢- X2¢ |
|
имеет наглядный смысл. При этом неизвестные X1¢ и X2¢ соответствуют новой основной системе (рис. 4.10, в), для которой эпюры`M10¢ и`M20¢ ортогональны (рис. 4.10, г, д), а d12¢ = 0, поэтому соответствующая система канонических уравнений распадается на два независимых уравнения:
d11¢ X1¢ + D1p0¢ = 0;
d22¢ X2¢ + D2p0¢ = 0.
Определив групповые или обобщенные неизвестные X1¢и X2¢, можно с по-
мощью (4.13) вернуться к старым переменным X1 и X2.
Разложение нагрузки на симметричную и обратносимметричную рас-
смотрим на следующем примере (рис. 4.11, а), где в соответствии с принципом суперпозиции в такой форме представлена заданная нагрузка (рис. 4.11, б, в). Для выбранной основной системы (рис. 4.11, г) d12 = 0 и расчет от симметричной нагрузки приводит к системе канонических уравнений:
|
d11 |
X1(1) |
+ D1p0(1) = 0; |
(4.14) |
|
d22 |
X2(1) |
= 0. |
|
При этом D2p0(1) = (`M20 ´ Mp0(1)) = 0 в силу ортогональности обратносим- |
||||
метричной эпюры `M 0 |
и симметричной эпюры M 0(1) |
от первого загружения |
||
2 |
|
|
p |
|
(рис. 4.11, б). Поэтому решением (4.14) будет X1(1) ¹ 0, X2(1) = 0.
Расчет рамы от второго варианта загружения (рис. 4.11, в) приводит к системе канонических уравнений:
