Рисунок 5 – Пример функционального свойства: имеетБиологическуюМаму
Рисунок 6 – Обратное функциональное свойство
являетсяБиологическойМатерью |
18 |
|
Транзитивные Свойства
Если свойство транзитивно и связывает отдельные индивиды а и б, а также индивид б с индивидом с, то мы можем сделать вывод, что индивид а связан этим же свойством с индивидом с. Например, рис. 7 показывает пример транзитивного свойства имеетПредка. Если Мэтью является предком Петра и Петр – предок Уильяма, то можно сделать вывод, что Мэтью – предок Уильяма, – на это указывает пунктирная линия на рисунке 7.
Рис. 7 – Пример транзитивного свойства: имеетПредка
Симметричные свойства
Если свойство P является симметричным и свойство связывает индивида а с
индивидом б, то б также связан с индивидом а с помощью того же свойства Р.
Рис. |
8 |
показывает |
пример |
симметричного |
свойства. |
Если |
индивид |
Мэтью связан |
с индивидом Джеммой через |
свойство |
имеетБратаИлиСестру, то мы можем заключить, что Джемма также должна быть связана с Мэтью через свойство имеетБратаИлиСестру.
Рис. 8 – Пример симметричного свойства: имеетБратаИлиСестру
Асимметричные свойства
Если свойство P является асимметричным и связывает индивида а с индивидом б, то индивид б не может быть связан с индивидом а через
свойство |
Р. |
Рис.9 показывает пример асимметричного свойства. Если |
индивид |
Жан связан с индивидом Мэтью через свойство являетсяРебенком, |
то можно |
утверждать, что Мэтью не может являться ребенком Жана, а |
потому не может быть связан с Жаном свойством являетсяРебенком. Это, однако, не мешает Мэтью быть связанным с другим лицом Биллом через
свойство являетсяРебенком.
Рис. 9 – Пример асимметричного свойства являетсяРебенком
Рефлексивные свойства
Свойство Р называется рефлексивным, когда это свойство связывает индивида с самим собой. На рис.10 мы видим пример рефлексивного свойства знает,
Джордж знает Джорджа, т.е. самого себя. Однако, кроме того, Джордж может знать других людей, поэтому Джордж может быть связан отношением знает с индивидом Симоном.
Рисунок 10– Пример рефлексивного свойства |
Рисунок 11– Пример иррефлексивного свойства |
знает |
являетсяМамой |
Иррефлексивные свойства
Если свойство иррефлексивное, то оно может быть описано как свойство, которое связывает индивида а с индивидом б, только когда эти индивиды различны. Как пример рассмотрим свойство являетсяМамой: индивид Алиса может быть связан с индивидом Бобом свойством являетсяМамой, но Алиса не может быть мамой самой себе (рис. 11).
Домены и диапазоны свойств
Свойство описывает бинарное отношение. Доменом называется область определения отношения, а диапазоном – область значений отношения. Свойства (отношения) связывают индивидов из домена с индивидами диапазона.
Применение онтологий
Ряд способов использования онтологий:
•для совместного использования людьми или программными агентами общего понимания структуры информации;
•для возможности повторного использования знаний в предметной области;
•для того чтобы сделать допущения в предметной области явными;
• для отделения знаний в предметной области от оперативных знаний;
• для анализа знаний в предметной области.
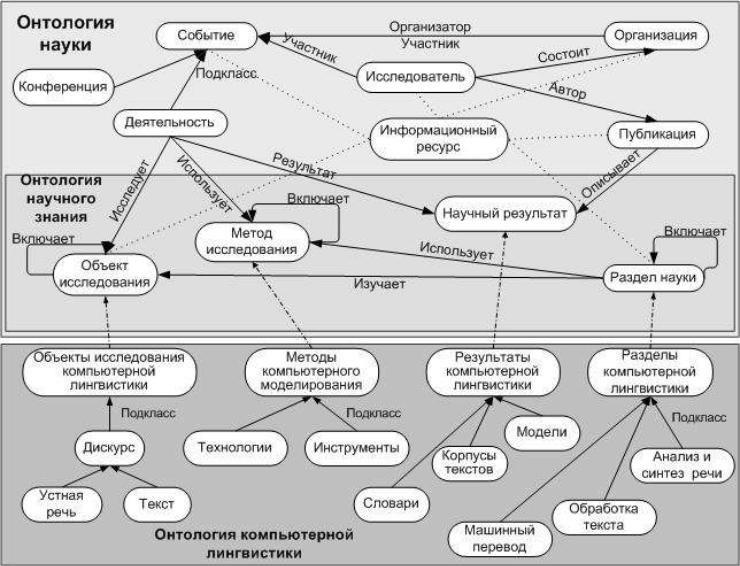
Рисунок 12 – Пример онтологии как научного знания и компьютерной лингвистики
Построение онтологии часто не является само по себе конечной целью, обычно онтологии далее используются другими программами для решения практических целей. На данном этапе развития науки существует ряд задач,
где применение онтологий может дать хорошие результаты. Однако сейчас
лишь малое количество приложений на естественном языке включают в себя онтологические базы, откуда черпаются знания об окружающей действительности. Использование онтологий возможно в:
•машинном переводе;
•вопросно-ответных системах;
•информационном поиске;
•системах извлечения знаний;
•общих системах ведения диалога между компьютером и
человеком;
•системах понимания языка (автоматическое реферирование текста, рубрикация и др.)