10307

В этом случае sin x и cos x выражаются по известным тригонометрическим

Заметим, что применение универсальной подстановки часто приводит к достаточно громоздким выражениям, поэтому использовать ее нужно только после того, как исчерпаны другие возможности.

Лекция 31. Комплексные числа

31.1. Введение. Вспомним, как развивалось понятие числа, начиная от чисел натуральных до чисел действительных. Если операция сложения во множестве натуральных чисел выполнима без ограничений, то операция обратная сложению, т.е. решение уравнения a x b , выполнима только при

220

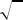
b a . Если отказаться от этого ограничения, то получатся «новые» числа – отрицательные. Так «родились» целые числа, во множестве которых сохранены все свойства суммы и обратная операция – разность, результатом которой является число x b a .

Во множестве натуральных чисел также не всегда разрешима задача,

ходимость расширения множества целых чисел до чисел рациональных. В этом множестве обратная операция – деление, результатом которой является число x b : a , разрешима с ограничением a 0 . Для рациональных чисел сохраняются свойства операций сложения и умножения.

Оказалось, что во множестве рациональных чисел не всегда разрешима задача извлечения квадратного корня из положительного числа,

например, неразрешимо уравнение x2 2 0 . Число 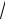2 , которым мы привычно обозначаем один из корней этого уравнения, число – иррациональное. Это число «должно» бы выражать длину диагонали квадрата со стороной равной единице. Но среди известных чисел, с помощью которых можно выразить длину диагонали, такого числа не нашлось. Такие числа назвали иррациональными, т.е. невыразимыми. Это открытие было сделано во времена Пифагора (580–500 г. до н.э.). Позднее, примерно через 1000 лет, латинские слова рациональный и иррациональный стали связывать со словом рацио – разум. В средневековой математической культуре возник новый термин вместо «иррациональный» – surdus (глухой или немой), т.е. такое число, когда немой его не может высказать другому, а второй (глухой) не может выслушать первого. Сопротивление «разума» исчезло, когда стали интерпретировать иррациональные числа бесконечными десятичными непериодическими дробями.

Комплексные числа, о которых пойдет речь, возникли из необходимости извлечения квадратного корня из отрицательного числа. Определим «новое» число –«мнимую единицу» i , квадрат которого равен 1, т.е.

i 2 1. Расширим множество действительных чисел, вводя числа вида

ный) частью комплексного числа, а число y Im z Im(x iy) его мнимой

(лат. imaginarius – мнимый) частью.

31.2. Геометрическая интерпретация комплексных чисел. Ком-

плексные числа удобно изображать точками плоскости xOy , с декартовой

системой координат, которую в этом случае называют комплексной плоскостью. Ось абсцисс этой плоскости называют действительной осью – ей отвечают действительные числа z x , а ось ординат – мнимой осью. Числа z iy , лежащие на мнимой оси, называют чисто мнимыми.

221

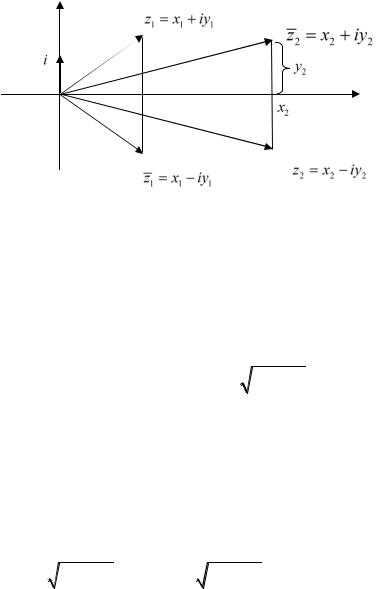
Два комплексных числа z1 x1 iy1 и z2 x2 iy2 равны тогда и только

тогда, когда x1 x2 и y1 y2

Сопряжённым к данному комплексному числу z x iy назовем число z x iy , которое обычно помечается чертой сверху. Сопряжённые комплексные числа отличаются знаком мнимой части. Если z x iy , то z x iy . Сопряжённые числа симметричны относительно действительной оси (см. рис. 31.1).

Рис. 31.1

31.3. Тригонометрическая форма комплексного числа. Наряду с ал-

Модуль – это расстояние от начала координат до точки z (x, y) .

Угол между положительным направлением оси Ox и радиус-векто- ром z называется аргументом комплексного числа. Поскольку этот угол определяется с точностью до числа, кратного 2 , то выделим его главную

222

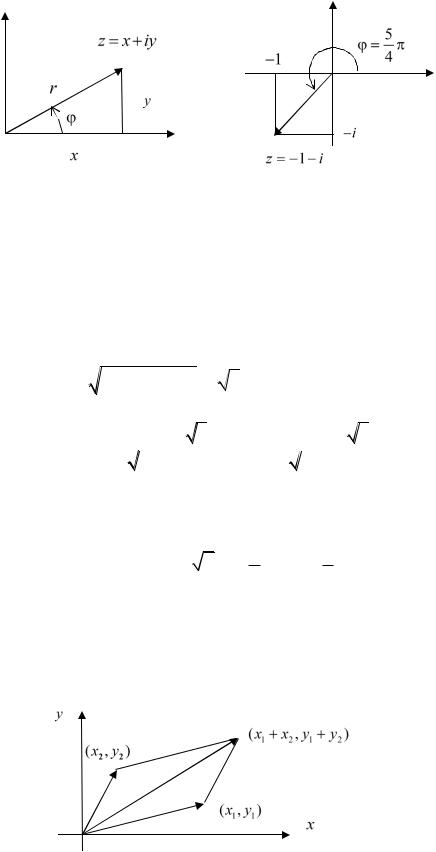
Рис. 31.2

От алгебраической формы комплексного числа легко перейти к его тригонометрической форме

рис. 31.2). Таким образом,

z1 i 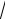2(cos 54 i sin 54 ) .

31.4.Операции над комплексными числами. Начнем со сложения.

Рис. 31.3

Заметим, что это соответствует правилу сложения векторов (см. рис. 31.3).

223

Произведением комплексных чисел называется число

(x1 iy1 ) (x2 iy2 ) (x1x2 y1y2 ) i(x1 y2 x2 y1 ) .

Найдём произведение двух комплексных чисел, заданных в тригонометрической форме

z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 )

r1 r2 (cos 1 cos 2 sin 1 sin 2 i(sin 1 cos 2 cos 1 sin 2 ))

r1r2 (cos( 1 2 ) i(sin( 1 2 )) .

Таким образом, при умножении комплексных чисел в тригонометрической форме их модули нужно перемножить, а аргументы сложить.

Геометрический смысл умножения на комплексное число

z r(cos i sin )

состоит в том, что происходит «растяжение» плоскости с коэффициентом r и поворот на угол . Благодаря этим свойствам комплексных чисел с их помощью удаётся решать задачи теории упругости, связанные с деформацией твёрдых тел, а также изучать движение жидкостей и газов.

Пример. Найти произведение чисел z1 2(cos(30 i sin30 ) и

z2 2(cos(120 i sin120 ).Умножение в тригонометрической форме даёт

В результате умножения вектора z1 на вектор z2 длина вектора z1 увеличилась в два раза и он «повернулся240 » на угол300120 (см. рис. 31.4).

270

224

После этого становится понятными правила умножения отрицательных чисел. Почему, например, ( 1) ( 1) 1? Действительно, представляя1 в тригонометрической форме, получаем

( 1)( 1) (cos i sin ) (cos isin ) (cos 2 isin 2 ) 1.

Также перестаёт быть «таинственной» формула i 2 1, поскольку

i i (cos 2 i sin 2 )(cos 2 i sin 2 ) (cos i sin ) 1.

Чтобы получить частное двух комплексных чисел, нужно умножить и числитель и знаменатель дроби на число сопряжённое знаменателю и отделить вещественную и мнимую части.

Найдём частное двух комплексных чисел, заданных в тригонометрической форме

r1 (cos 1 cos 2 sin 1 sin 2 i(sin 1 cos 2 cos 1 sin 2 )) r2

r1 (cos( 1 2 ) i sin( 1 2 )). r2

Итак, модуль частного двух комплексных чисел равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

ставим каждое из этих чисел в тригонометрической форме:

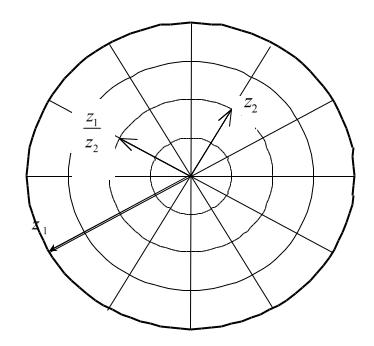
Тогда частное равно z1 / z2 2(cos1500 i sin1500 ) 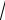3 i (см. рис. 31.5).

225

Определим операцию возведения в степень комплексного числа. По правилу умножения комплексных чисел в тригонометрической форме для всякого натурального числа n имеем

zn rn (cos n i sin n ) .

В частном случае, когда модуль числа равен единице, получается формула, носящая имя английского математика А. Муавра (1667-1754)

(cos i sin )n cos n isin n .

Эта формула служит источником для получения многих замечательных соотношений, связывающих тригонометрические функции. Например, при n 2 имеем равенство

cos2 2isin cos sin2 cos2 isin 2 .

Приравнивая действительные и мнимые части, получаем известные формулы для синуса и косинуса двойного аргумента

226

Лекция 32. Решение алгебраических уравнений

32.1. Извлечение корня из комплексного числа. Число z называется корнем n -ой степени из комплексного числа a , если zn a . Эта опера-

ция – обратная возведению комплексного числа в целую положительную степень. Во множестве вещественных (действительных) чисел эта задача

? В этой форме уравнение примет вид

rn (cos i sin )n | a | (cos isin )

или

rn (cos n i sin n ) | a | (cos isin ) .

Два комплексных числа в тригонометрической форме равны тогда и только тогда, когда их модули равны, а аргументы отличаются на число, кратное 2 , т.е.

rn | a |, n 2 k, k 0, 1, 2, .

Поэтому все корни имеют один и тот же модуль r n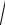 | a | , а аргументы этих корней определяются по формуле

Убедимся, что число корней конечно и равно показателю n степени уравнения. Действительно, представляя искомые корни в тригонометрической форме

видим, что в силу периодичности тригонометрических функций достаточно

их геометрическая интерпретация: все корни расположены на окружности,

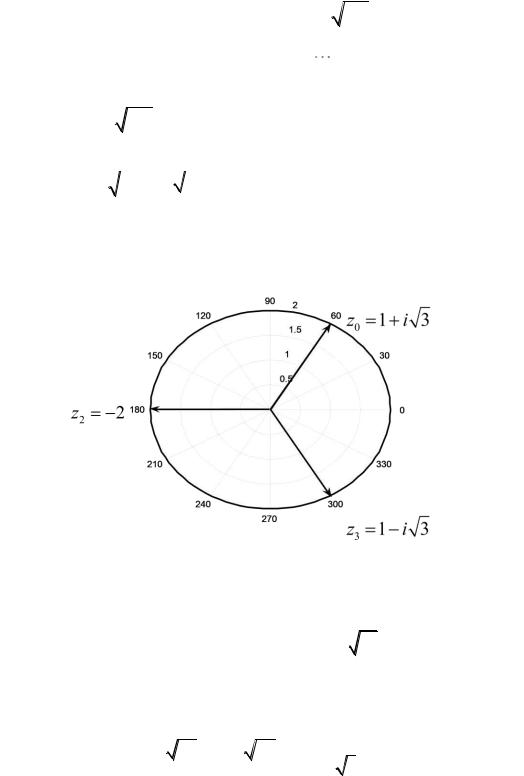
Например, уравнение z3 8 0 имеет три корня, расположенных на окруж-

положительным корнем из положительного числа. Если расширить его применение для изображения корня из комплексного числа, то он потеряет однозначность. Например,

32.2.Квадратное уравнение. Рассмотрим квадратное уравнение

ax2 bx c 0 , коэффициенты которого действительные числа. Формально написанная формула для вычисления его корней

во множестве действительных чисел не имеет смысла, если подкоренное вы-

Следовательно, если дискриминант уравнения отрицателен, то

b2 4ac (4ac b2 ) i 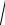| b2 4ac | .

Формула вычисления корней квадратного уравнения принимает вид

Пример. Решить уравнение z3 8 0 . После разложения левой части уравнения на множители

(x 2)(x2 2x 4) 0

229