10297

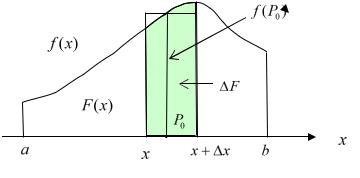
значение интеграла через длину промежутка интегрирования и значение подынтегральной функции в некоторой (правда неопределённой) точке этого промежутка.

Этот результат называют теоремой о среднем в интегральном исчислении.

33.4. Существование первообразной функции. В предыдущей лекции мы отметили, что интеграл непрерывной на [ a,b] функции

существует. Наша цель – связать понятия определённого и неопределённого интегралов и, тем самым, показать, как вычисляется определенный интеграл без вычисления интегральных сумм.

Рассмотрим интеграл с переменным верхним пределом

F (x) x f (t)d t ,

a

где подынтегральная функция f (x) непрерывна в промежутке [ a,b] .

Напомним, что переменная интегрирования – «немая», т.е. может быть обозначена любой буквой. Написанный нами интеграл – это некоторая функция F (x) верхнего предела x , и её геометрический смысл ясен из

следующего рисунка:

Рис. 33.6

Применяя теорему о среднем значении функции, запишем приращение в виде

f (t)d t F (b) F (a) .

a

Лекция 34. Вычисление определённого интеграла

34.1. Интегрирование по частям и замена переменной. Пусть u(x) и v(x) – функции, непрерывные вместе со своими производными в

Это и есть формула интегрирования по частям в определённом интеграле. Как и в случае неопределённого интеграла, её целесообразно применять, если интеграл справа будет «проще», чем исходный интеграл.

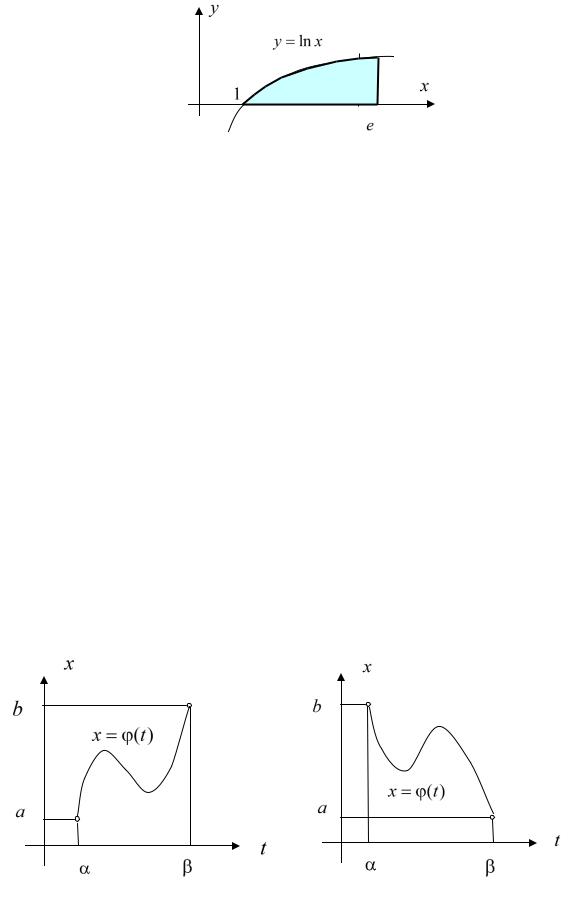
Пример. Найти площадь фигуры, ограниченной линией y ln x ,

осью абсцисс и прямой x e . Искомая площадь (см. рис. 34.1) выражается

e

интегралом S ln x d x

1

242

Формула Ньютона – Лейбница даёт возможность установить правило замены переменной в определённом интеграле. Пусть требуется вычислить интеграл

b

f (x)d x ,

a

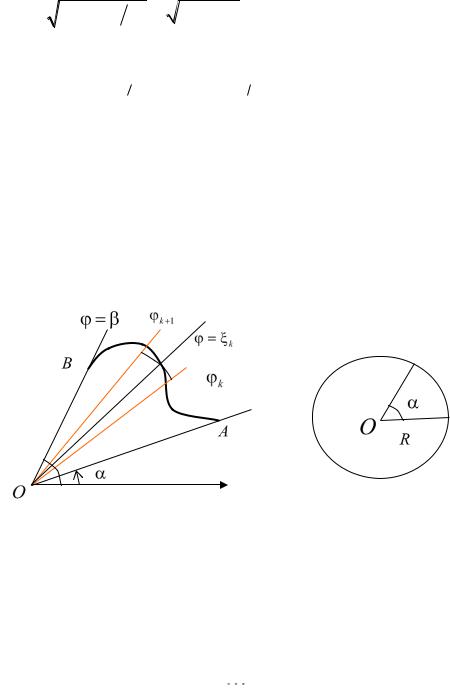
где функция f (x) непрерывна в промежутке [ a,b] . Пусть функция x (t) удовлетворяет следующим условиям: 1) (t) непрерывна вместе со своей производной (t) в некотором промежутке [ , ]; 2) сложная функция f ( (t)) должна быть определена в этом промежутке (для этого достаточно, например, потребовать, чтобы (t) была монотонна); 3) концам промежутка [ , ] соответствуют концы промежутка [ a,b] ,т.е. ( ) a,( ) b или ( ) b , ( ) a (см. рис. 34.2).

Рис. 34.2

243

При этих условиях имеют место формулы

Ft ( (t)) F ( (t)) (t) f ( (t)) (t) .

Применяя формулу Ньютона – Лейбница к обоим интегралам в первом из

b

равенств (34.1), получим, с одной стороны, f (x)d x F (b) F (a) , а с

a

другой

f ( (t)) (t)d t F ( (t) F ( ( )) F ( ( )) F (b) F (a) .

Аналогично можно убедиться в справедливости второго равенства в (34.1). Следует заметить, что, в отличие от замены переменной в неопределённом интеграле, здесь нет необходимости возвращаться к «старой» переменной. Если вычислены правые из интегралов (34.1), то, тем самым, вычислены и левые интегралы. Излишне упоминать, что не каждая подстановка ведёт к упрощению: какую замену переменной следует

применять –это может подсказать лишь опыт.

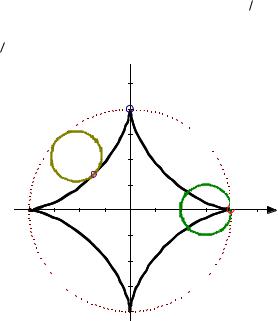
Пример. Вычислить площадь, ограниченную эллипсом, заданным

244

Опыт вычисления неопределённых интегралов «подсказывает» замену

34.2. Вычисление площади фигуры в полярной системе координат.

Аналогом криволинейной трапеции в полярной системе координат будет криволинейный сектор. Это фигура, ограниченная лучами , и кривой AB , заданной уравнением ( ) , определяющим для каждого значения угла расстояние от начала координат до соответствующей точки кривой AB (см. рис. 34.3).

Рис. 34.3

Предполагается, что функция ( ) непрерывна в промежутке, . Будем сначала решать задачу вычисления площади криволинейного

равным ( k ) , k [ k , k 1] . Площадь кругового сектора радиуса R и с центральным углом равна

Sсект. 12 R2 .

Поэтому площадь сектора OAB приближённо выражается интегральной суммой

S1 n 2 ( k ) k .

2 k 1

Переходя к пределу при n , причём так, что длина максимального из

частичных отрезков max( k ) стремится к нулю, получаем

k

Рис. 34.4

Если вычисленияпроводить в декартовой системе координат, то получается «плохой» интеграл

Перейдём к полярным координатам по формулам: x cos , y sin .

Пример 2. Вычислить площадь, ограниченную одним витком спирали Архимеда и полярной осью. Спираль Архимеда можно рассматривать как траекторию точки, равномерно движущуюся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается вокруг полюса. В полярнойсистеме координат её уравнение имеет видa , a 0, a const . Один виток спирали получается при повороте луча

на угол 2 .Искомая площадь выражается интегралом

Рис. 34.5

34.3. Вычисление площади фигуры, ограниченной кривыми,

заданными параметрически. Интерпретируя определённый интеграл площадью криволинейной трапеции, мы предполагали, что кривая y f (x)

задана в явном виде. А как быть, если границы фигуры заданы параметрическими уравнениями? Заметим, что задание кривой в явном виде

– это частный случай её параметрического задания, когда в качестве параметра избрана переменная x :

Лекция 35. Другие приложения определённого интеграла

В предыдущей лекции мы применили определенный интеграл к вычислению площадей фигур. Здесь будут рассмотрены другие его приложения.

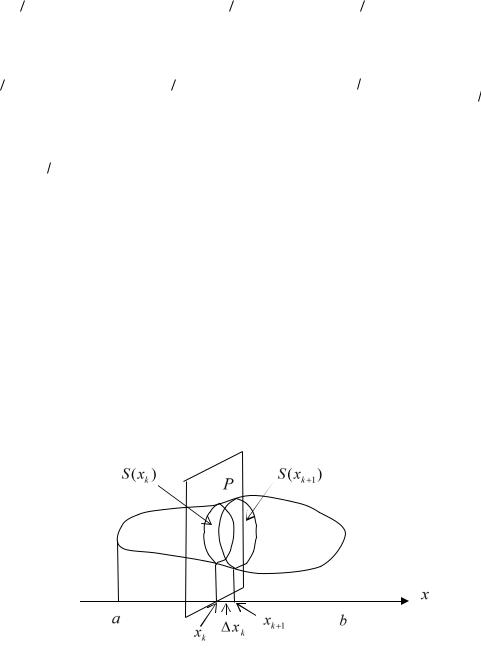
35.1. Вычисление объёма тела с известной площадью поперечного сечения. Пусть некоторое тело в направлении оси абсцисс находится в пределах отрезка [ a,b] . Как обычно, разбиваем этот отрезок на n частей

и через точки деления проводим плоскости P , перпендикулярные оси Ox

. Эти плоскости рассекут тело на «дольки». На рисунке изображена одна из них.

«дольки» можно приближённо вычислить как объём цилиндра с площадью основания S (xk ) и высотой xk . Поэтому объём тела приближённо равен

сумме объёмов таких цилиндров

n

V S (xk ) xk

k 1

249