
10292
.pdf
Раздел 6. Математический анализ. Интегральное исчисление
Лекция 29. Неопределенный интеграл
Наряду с задачейдифференцирования функции, в которой для заданной функции f (x) требуетсянайти ее производную f (x) , часто приходится
решать обратную задачу, называемую интегрированием функции: для заданной функции f (x) найти такую функцию F (x) , производная которой
совпадает с функцией f (x) , т.е. |
|
|
|
|
|
|
|
|
F (x) f (x) . Например, предполагая, что |
||||||||
известно уравнение движения |
S S (t) , т.е. закон изменения |
пути с |
||||||
течением времени, можно найти |
|
|
|
Если, |
напротив, |
|||
скорость v(t) S (t) . |
||||||||
заданаскорость как функция времени |
v v(t) , то |
возникает |
задача об |
|||||
определении пройденного пути |
|
S |
в |
зависимости |
от |
времени, |
т.е. по |
|
функции v v(t) «восстановить» |
|
функцию S(t) , |
для |
которой |
v v(t) |
|||
является производной S (t) v(t) . |
В данной лекции рассмотрим решение |
|||||||
этой обратной задачи.Происхождение термина интегрирование связано с именем Я. Бернулли (1654-1705). Вероятно, он произвёл термин от латинскогоintegro – приводить в прежнее состояние, восстанавливать.
29.1. Первообразная функция и неопределённый интеграл.Функция
F (x) называется первообразнойфункции f (x) на промежутке (a,b) , если для любого x (a,b) выполняется равенство
dF (x) f (x) . dx
К сожалению, это определение не даёт способа нахождения первообразной F (x) данной функции f (x) . Однако для основных
элементарных функций эта задача разрешима, поскольку известны их
производные. |
Например, |
|
легко |
видеть, |
что |
первообразной |
функции |
|
f (x) cos x будет функция |
F (x) sin x ,так |
как |
(sin x)' cos x . Но для |
|||||
функции f (x) cos x |
есть |
и |
другие |
первообразные. |
Например, |
|||
F (x) sin x 1, |
F (x) sin x 2 |
и, |
вообще, |
F (x) sin x C , где |
C – любое |
|||
число.
Из этого примера следует, что одна и та же функция имеет множество первообразных.Возникает вопрос – как найти всё это множество? Покажем,
210

что множество |
функций |
F (x) C , |
где F (x) – некоторая первообразная |
функции f (x) , |
а C – |
произвольная постоянная, исчерпывает все |
|
первообразныефункции f (x) . |
|
||
Теорема.Если F1 (x) |
и F2 (x) |
– двепервообразные функции f (x) ,то |
|
F1 (x) F2 (x) C , где C –некоторая постоянная. |
|||
Доказательство.Рассмотрим функцию (x) F1 x F2 (x) . Так как для |
|||
любого x имеем |
|
|
|
|
|
|
|
|
(x) F1 (x) F2 (x) f (x) f (x) 0 , |
||
то по формуле Лагранжа конечных приращений получаем, что (x) C , и,
следовательно, F1 x F2 (x) C .
Таким образом, достаточно найти одну первообразную F (x) данной функции f (x) , чтобы знать всё множество её первообразных F (x) C .
Для обозначения рассматриваемой операции – нахождения функции F (x) изравенства
dF (x) f (x)dx ,
был введён символ , применение которого к указанному равенству восстанавливает множество всех первообразных данной функции f (x)
(подобно тому, как знак 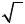 обозначает операцию нахождения квадратного корня). Для краткости совокупность всех первообразных функции f (x) называется её неопределенным интеграломи обозначается так
обозначает операцию нахождения квадратного корня). Для краткости совокупность всех первообразных функции f (x) называется её неопределенным интеграломи обозначается так
f (x) dx F (x) C ,
где C – некоторая постоянная.Операция нахождения неопределенного интеграла называется интегрированием.При этом функция f (x) называется
подынтегральной функцией, f x dx – подынтегральным выражением, а знак– знаком интеграла.
Поставим вопрос: для всякой ли функции f (x) существует
первообразная, а, следовательно, и неопределенный интеграл?
Сформулируем без доказательства достаточное условие интегрируемости:
если функция f (x) непрерывна на интервале (a,b) , то на этом множестве у функции f (x) существует первообразная, а, значит, и неопределённый
интеграл. Ниже будем говорить об интегралах непрерывных функций, которые заведомо существуют.
211

Из определения неопределенного интеграла непосредственно следуют формулы, подчёркивающие, что операции интегрирования и дифференцирования взаимно обратные (с точностью до постоянной)
f (x)dx f x , |
d f x dx f x dx , |
|
df (x) f (x) C . |
f (x)dx f (x) C , |
Это аналогично тому, как операции возведения в целую степень и извлечение корня, проведённые последовательно друг за другом, оставляют без изменения число, к которому они применялись
|
|
|
|
|
|
|
( n a )n a, |
n an a, |
a 0. |
||||
Отметим два свойства, непосредственно вытекающие из соответствующих правил дифференцирования: постоянный множитель можно выносить за знак интеграла, т.е.
k f (x) dx k f (x)dx k const ,
и неопределённый интеграл суммы или разности конечного числа функций равен соответствующей сумме (разности) интегралов этих функций, т.е.
( f (x) g(x))dx f (x)dx g(x)dx .
Для нахождения производной функции, полученной из основных элементарных функций с помощью алгебраических операций или суперпозиции, применялись таблица производных основных элементарных функций и правила дифференцирования. Формально, таблица интегралов элементарных функций может быть получена, если переписать справа налево таблицу производных. Однако для практического применения целесообразнее привести таблицу интегралов в следующем виде:
|
|
|
x 1 |
|
|
dx |
|
|
|
||
x |
dx |
|
|
C ( 1) , |
|
|
|
= ln |
x |
C |
|
|
|
|
x |
||||||||
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
axdx |
|
ax |
C (a 0, a 1) |
, |
|
exdx ex C |
|||||
|
|
|
|||||||||
|
|
|
ln a |
|
|
|
|
|
|
||
sin x dx cos x C cos x dx sin x C
212
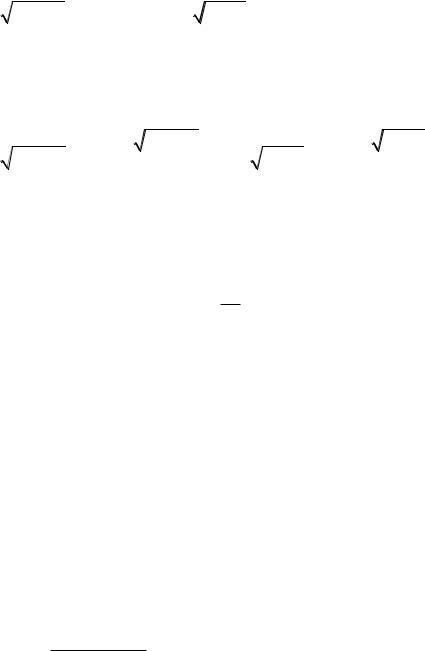

cosdx2 x sindx2 x tg x ctg x C ,
где при вычислении интеграла суммы нескольких функций сумма произвольных постоянных, которая при этом получается, заменена одной постоянной.
Следует отметить, что некоторые интегралы не могут быть выражены через элементарные функции. В частности, это касается интегралов следующих функций:
sin x |
, |
cos x |
, |
1 |
, e x2 . |
|
x |
x |
ln x |
||||
|
|
|
29.2.Интегрирование методами подстановки и замены переменной.Еще одно важное свойство неопределенного интеграла, основанное на инвариантности формы первого дифференциала, позволяет находить интегралы функций, не входящих в таблицу.
Пусть
f (x) dx F (x) C
иформально подставим в эту формулу функцию x (t) ,производная которой непрерывна. Тогда получим так называемую формулу подстановки
f ( (t)) (t)dt f ( (t))d (t) F( (t)) C .(29.1)
Покажем, что формула (29.1), действительно, верна. Для этого найдём производную по переменной t правой части этого выражения
|
|
|
|
|
|
Fx |
( (t)) (t) f ( (t)) (t) . |
||
Таким образом, |
правая |
часть |
в (29.1) |
является первообразной |
подынтегрального выражения слева.
Применение этой формулы позволяет находить интегралы сложных функций, используя таблицу основных интегралов. Например, найдем
cos(3x 2)dx .
Зная, что
cosudu sin u C
иделая в этойформулеподстановкуu 3x 2 , получим
214

cos(3x 2)d (3x 2) sin(3x 2) C ,
откуда найдем
cos(3x 2)dx 13 sin(3x 2) C .
Этот прием, основанный на подстановке некоторой функции в готовую формулу табличного интеграла, называют методом подстановки.
Рассмотрим теперь приём интегрирования с помощью замены переменной. Предположим, что нужно найти интеграл f (x)dx . Заменяем
переменную интегрирования некоторой дифференцируемой функцией x (t) , имеющей обратную функцию t (x) . Предположим также, что
(t) непрерывна.Тогда справедлива формула замены переменной в
неопределенном интеграле
|
(29.2) |
f (x)dx f ( (t)) (t)dt , t (x) . |
|
Действительно, пусть F (x) первообразная |
f (x) . Тогда по формуле |
подстановки правая часть этого выражения равна |
|
f ( (t)) (t)dt F( (t)) C F(x) C
при x (t) , что подтверждает справедливость формулы (29.2).
Прием замены переменной состоит в том, чтобы после её проведения сделать такую замену, при которой для подынтегральной функции в полученном интеграле справа в (29.2) легко может быть найдена первообразная.
|
|
|
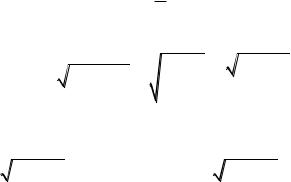
Например, для нахождения интеграла |
a2 x2 dx сделаем замену |
|
переменной x a sin t так, что

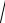 a2 x2
a2 x2 
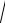 a2 a2 sin2 t a cost , dx a cost dt .
a2 a2 sin2 t a cost , dx a cost dt .
Следовательно,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos 2t |
|
a |
2 |
x |
2 |
dx a |
2 |
cos |
2 |
tdt |
a |
2 |
|
dt |
|||||||
|
|
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
1 |
|
|
|
|
|
a2 |
t sin t cost C . |
||||||||
|
|
|
|
t |
|
|
|
sin 2t |
|
C |
|
||||||||
2 |
|
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
215 |
|
|
|
|
|
|
|
|
Перейдём от переменной t к переменной x . В промежутке a x a
существует обратная функция t arcsin ax , поэтому
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x2 |
|
|
|
a2 x2 |
. |
||||||
|
cost |
1 sin2 t |
|
||||||||||||||||
|
a2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||
Окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dx |
a2 |
arcsin |
x |
|
x |
|
|
|
||||||||
|
|
a2 x2 |
|
a2 x2 |
C . |
||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
a |
2 |
|
|
|
|
|
|||||
Заметим в заключение этой темы, что в некоторых случаях замену переменной непосредственно не осуществляют, а применяют так называемую операцию «внесения под дифференциал». Заменяя выражение(x)dx дифференциалом d (x) , получают
f ( (x))d (x) f ( )d .
Например, |
|
|
|
||||
|
1 |
|
1 |
|
3x 7 |
11 |
|
3x 7 10dx |
3x 7 10 d 3x 7 |
|
|
|
C . |
||
3 |
3 |
11 |
|
||||
216
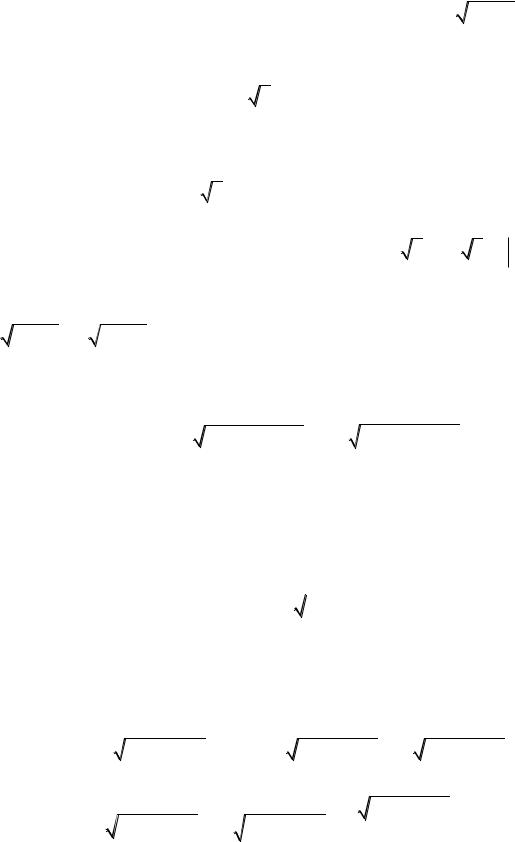
Лекция 30. Методы интегрирования (продолжение)
30.1.Интегрирование простейших иррациональностей.Рассмотрим только простейшие случаи иррациональных подынтегральных функций.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если интеграл |
содержит иррациональность |
вида |
n ax b a 0 , то |
||||||||||||||||||||||||
применяют подстановку |
ax b tn . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример.Найти интеграл |
|
|
1 |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Сделаем замену или x t2 . Тогда |
dx 2tdt и |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
|
dx |
2t dt |
2 |
t 1 1 |
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
x 1 |
|
|
|
|
|
t 1 |
|
t 1 |
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 t |
|
|
dt 2 t ln |
t 1 |
C = 2( |
|
x ln |
|
|
x 1) C . |
|||||||||||||||||
t 1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Если |
подынтегральное выражение |
содержит иррациональностивида |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b t p с p , |
||
n ax b и |
m ax b , где |
m n , то применяют подстановку |
|||||||||||||
равным наименьшему общему кратному чисел m и n . |
|
||||||||||||||
|
Рассмотрим интегралы вида |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
dx |
|
Mx N dx |
|
|||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Ax2 Bx C |
|
|
Ax2 Bx C |
|
|||||
Первый из них сводится к табличному интегралу выделением полного квадрата в подкоренном выражении. Для нахождения второго интеграла следует в числителе выделить дифференциал квадратного трехчлена d ( Ax2 Bx C) (2Ax B)dx .
Пример. Найтиинтеграл I |
x 2 dx |
|
|
. |
||
|
|
|
|
|
||
3 |
2x x |
2 |
||||
|
|
|
|
|||
В числителе дроби получим дифференциал подкоренного выражения d (3 2x x2 ) (2 2x)dx и разобьём интеграл на два интеграла
I |
1 |
|
(2 2x) 2 |
|
dx |
|
1 |
|
|
(2 2x)dx |
|
|
dx |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 2x x2 |
3 2x x2 |
3 2x x2 |
|
|||||||||||||||||||||||||
|
1 |
|
|
d (3 2x x2 ) |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
2x x2 arcsin |
C |
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
3 2x x2 |
|
4 (x 1)2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
217 |
|
|
|
|
|
|
|
|
|
|
|
|

Винтегралах вида

 a2 x2 dx ,
a2 x2 dx , 
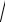 a2 x2 dx ,
a2 x2 dx , 
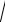 x2 a2 dx
x2 a2 dx
освобождаются от иррациональности применением тригонометрических подстановок. Для первого интеграла применяется замена x a sin t (можно
x acost ) |
и используется тождество |
sin2 t cos2 t 1; |
для второго – |
|||||
замена x a tgt и применяется соотношение 1 tg2 t |
1 |
; для третьего – |
||||||
cos2 t |
||||||||
|
|
|
|
|
|
|
||
замена x |
a |
или x |
a |
. |
|
|
|
|
cos t |
sin t |
|
|
|
||||
|
|
|
|
|
|
|||
30.2. Интегрирование по частям.Рассмотрим метод интегрирования, который позволит нахождение одного интеграла заменить отысканием другого, «более простого». В основу этого метода положено следующее рассуждение. Пусть u (x) и v(x) – две функции, имеющие непрерывные
производные на некотором интервале. Найдем дифференциал d (u v) от произведения этих функций
d (u v) u dv v du ,
где dv v (x) dx, du u (x) dx . Перепишем это выражение в виде u(x) dv(x) d (u(x) v(x)) v(x)du(x)
и проинтегрируем обе его части. Учитывая, что d (u v) u v , получим
формулу интегрирования по частям
u(x) dv(x) u(x) v(x) v(x) du(x) .
Метод интегрирования по частям состоит в представлении интеграла
f (x)dx
ввиде u(x) dv(x) так, чтобы интеграл v(x) du(x) в правой части формулы
интегрирования по частям оказался «более простым». При нахождении функции v(x) можно произвольную постоянную C , возникающую при этом
интегрировании, положить равной нулю.
Найдем интеграл x e xdx . Введем обозначения: u(x) x ,
218
dv(x) e xdx . Тогда du(x) dx и v(x) e xd ( x) e x .
Применяя формулу интегрирования по частям, получим
|
x e xdx x e x e xdx x e x e x C . |
|
Формула |
интегрирования по частям |
предполагает разбиение |
подынтегрального выражения на два множителя |
u(x) и dv(x) , причем при |
|
переходе к правой части первый дифференцируется, а второй интегрируется. Нужно стараться, во-первых, чтобы интегрирование дифференциала dv не представляло трудностей и, во-вторых, чтобы
интеграл v(x) du(x) имел более простое подынтегральное выражение. Так,
в предыдущем примере было бы «неразумно» положить u e x , а |
dv xdx |
|||||
. Действительно, в этом случае |
|
|
|
|
|
|
x e xdx |
x2 |
e x |
1 |
x2 |
e xdx , |
|
|
|
|
||||
2 |
|
2 |
|
|
|
|
мы получили более сложный интеграл, чем первоначально данный. Заметим, что если мы имеем интегралы вида
Pn (x)sin kxdx , Pn (x)cos kxdx , Pn (x)ekxdx ,
( Pn x – многочлен n -ой степени), то следует выбрать u(x) Pn (x) . При
этом интегрирование по частям проводится столько раз, какова степень многочлена Pn (x) . Если же имеем интегралы вида
Pn (x)arcsin kx dx , Pn (x)arccos kx dx , Pn (x)arctg kx dx ,
Pn (x)arcctg kx dx , Pn (x)loga kx dx ,
то выбираем в качестве функции u(x) либо обратную тригонометрическую функцию, либо логарифм.
30.3. Интегрирование выражений, содержащих тригонометрические функции.Разнообразие тригонометрических функций и особенно формул, их связывающих, приводит к большому
219
