
10290
.pdf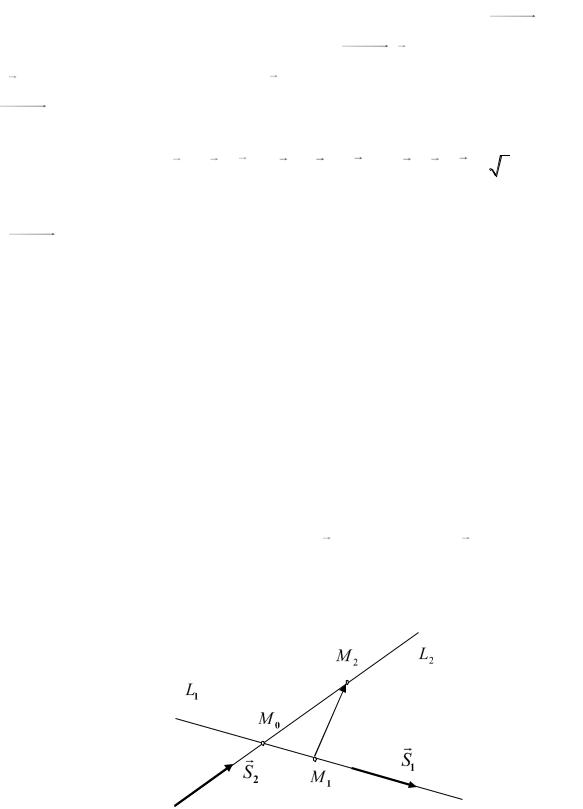
|
|
|
x |
|
y 7 |
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
5 |
2 |
|
|
|
|
|
||||
и найти её проекциюна эту прямую. |
|
|
|
|
|
|
|
|
|||||
Выберем |
точку |
на прямой |
|
M1 (0, 7, 2) , тогда M1M 0 |
{2,6,1}. |
||||||||
Вычислим скалярное произведение |
M1M 0 , S 38 , квадрат |
модуля |
|||||||||||
| S |2 38 направляющего вектора S {3,5, 2}, и по формуле |
(12.9)получим |
||||||||||||
M1M 2 {3,5, 2}: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
d | 2i 6 j k (3i 5 j 2k ) | | i j k | 3 . |
|
||||||||||||
Координаты проекции |
точки |
|
M 2 (x2 , y2 , z2 ) находим |
из равенства |
|||||||||
M1M 2 {x2 0, y2 |
7, z2 |
2} M 2 (3, 2, 4) , поэтому окончательно получаем |
|||||||||||
M 2 (3, 2, 4) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
В частности, таким способом можно находить расстояние между параллельными прямыми в пространстве как расстояние от точки, взятой на одной прямой, до другой прямой.
12.3. Пересечение прямых в пространстве. Пусть двепрямые L1 и L2
заданы каноническими уравнениями
L : |
x x1 |
|
y y1 |
|
z z1 |
, |
L : |
x x2 |
|
y y2 |
|
z z2 |
. |
|
|
|
|
|
|
||||||||
1 |
m1 |
|
n1 |
|
p1 |
2 |
m2 |
|
n2 |
|
p2 |
||
|
|
|
|
|
|
||||||||
Выясним условия пересечения этих прямых. Предполагаем, что направляющие векторы этих прямых S1 {m1, n1, p1} и S2 {m2 , n2 , p2} не
коллинеарны, что исключает случаи параллельности или совпадения этих прямых, и, кроме того, точки M1 (x1, y1, z1 ) и M 2 (x2 , y2 , z2 ) различные (см.
рис.12.6).
Рис. 12.6
90
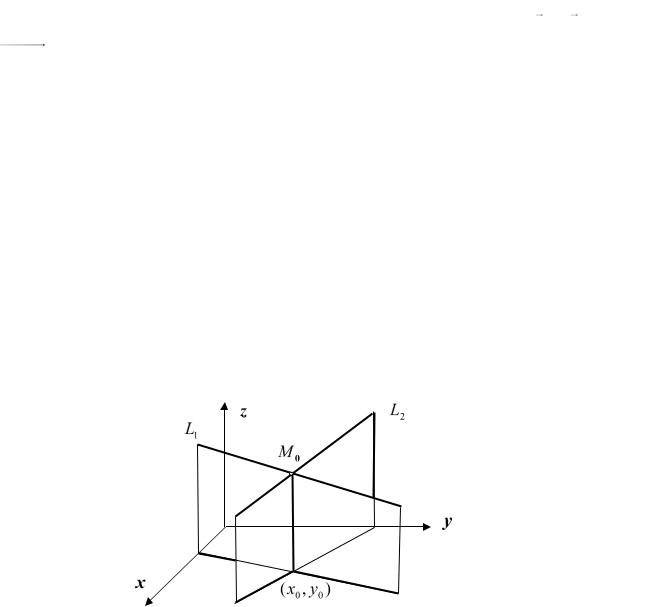
Ясно, что прямые будут принадлежать одной плоскости, а значит
пересекаться в точке M 0 , тогда и только тогда, |
когда три вектора S1 , S2 и |
||||
M1M2 {x2 x1, y2 y1, z2 z1} компланарны. В |
|
координатной форме это |
|||
условие выглядит так |
|
|
|
|
|
|
x2 x1 |
y2 y1 |
z2 z1 |
|
|
|
|
|
|||
|
m1 |
n1 |
p1 |
|
0 . |
|
m2 |
n2 |
p2 |
|
|
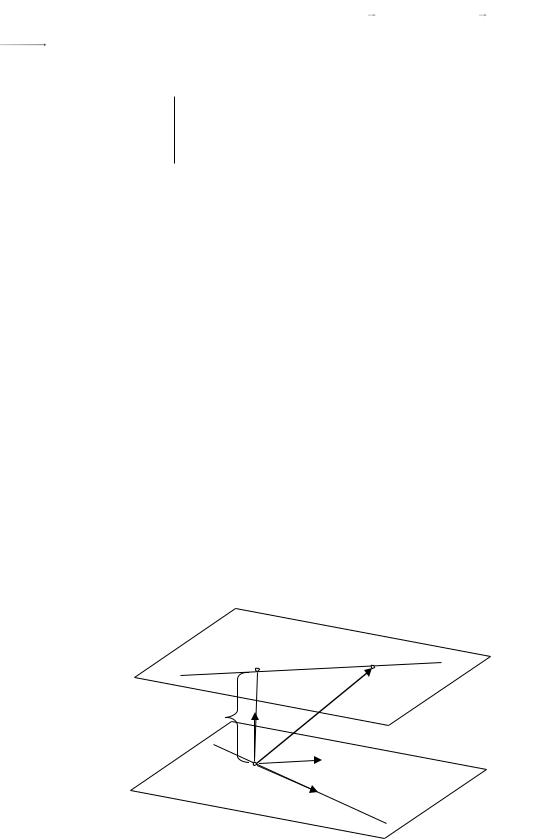
Как найти координаты точки пересечения прямых? Проведём через каждую прямую плоскость, проецирующую эту прямую на какую-нибудь из
координатных |
плоскостей. |
Например, |
рассмотрим |
плоскости, |
|
проецирующие эти прямые на плоскость |
xOy . |
Пересечение этих |
|||
плоскостей – это прямая, перпендикулярная плоскости |
xOy . Координаты |
||||
точки пересечения этой прямой с плоскостью |
xOy совпадают с |
||||
соответствующими координатами точки пересечения данных прямых (см.
рис. 12.7).
Рис.12.7
Нахождение координат точки (x0 , y0 ) сводится к решению системы
x x |
|
|
|
y y |
|
|
||||
|
1 |
|
|
|
1 |
|
|
|||
|
m1 |
|
|
n1 |
|
|
||||
|
|
|
|
|
|
, |
||||
|
|
x x |
|
|
|
|
y y |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
n |
2 |
|
||
|
2 |
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
2 |
|
|
||
а третья координатаможет быть найдена из уравнения прямой L1 или L2 . Пример. Доказать,что прямые
91
L : |
x 5 |
|
y 4 |
|
z 5 |
, L : |
x 5 |
|
y 16 |
|
z 6 |
|
||
|
|
|
|
|
|
|||||||||
1 |
3 |
|
6 |
2 |
2 |
4 |
|
|
12 |
3 |
|
|||
|
|
|
|
|
|
|||||||||
пересекаются и найти |
координаты |
точки их |
пересечения |
M 0 (x0 , y0 , z0 ) |
||||||||||
Проверяем компланарность тройки векторов S1 {3, 6, 2}, S2 |
{4, 12,3} и |
|||||||||||||
M1M 2 {0,12, 1} , вычисляя определитель:
|
|
|
|
|
|
|
|
|
|
|
0 |
12 |
1 |
|
6 |
2 |
|
3 |
6 |
|
0 . |
|
|
|
||||||||
3 |
6 |
2 |
12 |
|
|
|||||
4 |
12 |
3 |
|
12 |
3 |
|
4 |
12 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Следовательно,эти прямые пересекаются. Координаты точки пересечения находим, решая, например, систему
x 5 |
|
|
y 4 |
|
|||||
|
3 |
|
|
|
6 |
|
. |
||
|
|
x 5 |
|
|
|
y 16 |
|||
|
|
|
|
|
|||||
|
4 |
|
|
12 |
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Её решение x0 7, y0 20 . Из уравнения, допустим, первой прямой найдем третью координату z0 3 . Итак, точка пересечения этих прямых
M 0 (7, 20,3).
12.4. Расстояние между двумя прямыми.Случай параллельных прямых мы рассматривали в п.12.2. Поэтому пусть прямые скрещивающиеся, следовательно, расположены в параллельных плоскостях (см. рис. 12.8), расстояние между которыми и будет искомым расстоянием между прямыми.
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
1 |
1 |
|
1 |
92
Рис.12.8
Пусть прямые заданы каноническими уравнениями
L : |
x x1 |
|
y y1 |
|
z z1 |
, |
L : |
x x2 |
|
y y2 |
|
z z2 |
|
|
|
|
|
|
|||||||
1 |
m1 |
|
n1 |
|
p1 |
2 |
m2 |
|
n2 |
|
p2 |
|
|
|
|
|
|
|
|||||||
Кратчайшее расстояние между прямыми найдём как абсолютную величину
проекции вектора 1 2 |
на вектор |
= 1 |
× 2. |
|
|
|
||||||||
Пример. Найти расстояние между прямыми |
|
|
|
|||||||||||
|
+ 1 |
|
|
|
− 1 |
|
|
|
+ 1 |
|
− 2 |
|
||
1 : |
|
|
= |
|
= |
|
; |
2 : |
|
= |
|
= |
|
; |
1 |
|
1 |
2 |
1 |
3 |
4 |
||||||||
Вектор 1 2 = {1, −1, 1}. Находим векторное произведение
|
|
|
= 1 × 2 = |1 |
1 |
2| = −2 − 2 + 2 . |
1 |
3 |
4 |
Удобнее находить проекцию на вектор = {1, 1, −1}, коллинеарный вектору . Тогда
= Пр |
|
= |
∙ 1 2 |
= |
|1 − 1 |
+ 1| |
≈ 0.58. |
|
|
|
|
|
|||||
|
1 2 |
|
|
|
√3 |
|||
|
|
|
|
|||||
Лекция 13. Взаимное расположение прямых и плоскостей
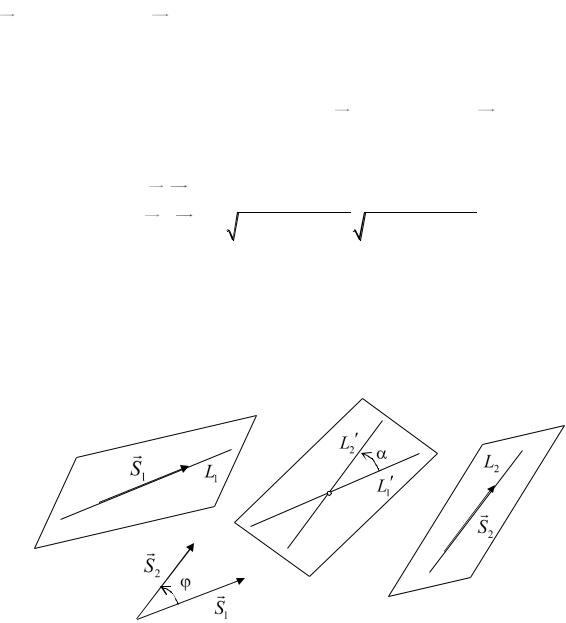
13.1.Угол между прямыми в пространстве. Пусть заданы две прямые
L1 и L2 своими каноническими уравнениями
L : |
|
x x1 |
|
|
y y1 |
|
z z1 |
|
|
|||
|
|
|
|
|
|
|||||||
1 |
|
m1 |
|
|
n1 |
|
|
|
p1 |
|||
|
|
|
|
|
|
|
||||||
L : |
x x2 |
|
y y2 |
|
z z2 |
. |
||||||
|
|
|
||||||||||
2 |
|
m2 |
|
|
n2 |
|
|
|
p2 |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
93 |
|
|
|
|
|
|
||
Если |
m1 |
|
n1 |
|
|
p1 |
|
, что означает коллинеарность направляющих векторов |
m2 |
n2 |
|
p2 |
|
||||
|
|
|
|
|
|
|||
S1 {m1, n1, p1} |
и |
|
S2 {m2 , n2 , p2}, то прямые L1 и L2 параллельны и угол |
|||||
между ними полагают равным нулю. Параллельные прямые, очевидно, принадлежат одной плоскости.
Под углом между пересекающимися прямыми будем понимать уголмежду их направляющими векторами S1 {m1, n1, p1} и S2 {m2 , n2 , p2}, если он острый, и угол в противном случае. Следовательно,
cos | cos | |
| S1 |
, S2 | |
|
|
| m1 m2 n1 n2 p1 p2 |
| |
|
. |
(13.1) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
S |
|
|
S |
2 |
|
m 2 |
n 2 |
p 2 |
|
m 2 |
n 2 |
p 2 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
||
Прямые, не лежащие в одной плоскости, называются |
|||||||||||||||||||
скрещивающимися |
|
прямыми. |
Определим |
понятие угла |
между |
||||||||||||||
скрещивающимися прямыми. Под углом |
между двумя прямыми L1 и L2 |
||||||||||||||||||
будем понимать наименьший из углов между пересекающимися прямыми L1 и L2 , им параллельными (см. рис.13.1).
Рис. 13.1
В частности, условие перпендикулярности двух прямыхимеет вид
L1 L2 m1m2 n1n2 p1 p2 0 .
13.2. Угол между прямой и плоскостью.Найдем теперь угол между прямой
L : |
x x0 |
|
y y0 |
|
z z0 |
(13.2) |
|
m |
n |
p |
|||||
|
|
|
|
и плоскостью П : Ax By Cz D 0 . Напомним, что под углом между прямой и плоскостью понимают наименьший положительный угол
94
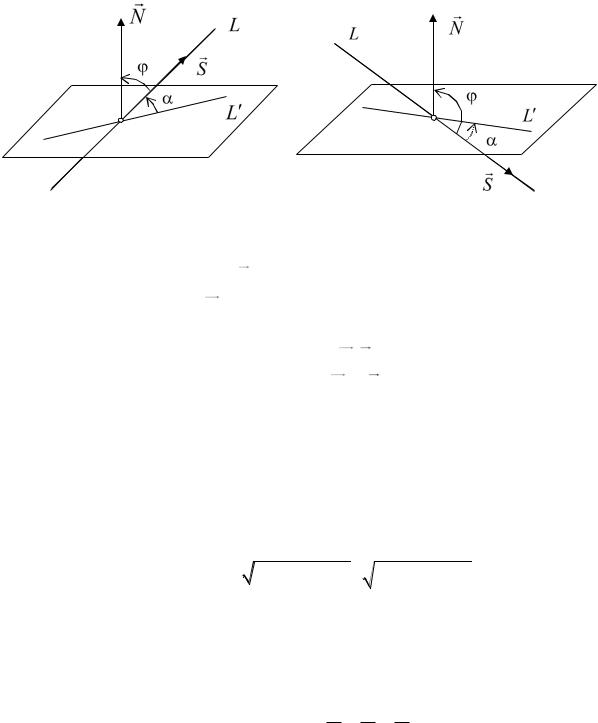
между проекцией |
|
прямой L на плоскость П и прямой L (см. рис. |
L |
||
13.2). |
|
|
|
Рис. 13.2 |
|
|
|
|
Вычисление угла |
можно свести к вычислению угла |
|
между |
||
направляющим вектором S {m, n, p} прямой |
L и нормальным к |
||||
плоскости П вектором |
N {A, B,C}. |
В случае острого угла |
0 / 2 |
||
имеем |
|
|
|
|
|
|
sin cos N, S . |
|
|
|
|
|
|
| N | | S | |
|
|
|
|
|
|
|
|
|
В случае тупого угла |
/ 2 , |
так как |
2 (см. рис. |
13.2), |
|
получим sin sin( 2 ) cos . Таким образом, для вычисления угла между прямой и плоскостью получаем формулу
sin | cos | |
|
|
| mA nB pC | |
|
. |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
A2 |
B2 C2 |
m2 n2 p2 |
||||||
|
|
|
|
|||||
В частности, условие перпендикулярности и условие параллельностипрямой и плоскостиимеют вид
L П mA Bn Cp ;
L || П Am Bn Cp 0 .
В последнем случае, если дополнительно выполняется равенство
95

Ax0 By0 Cz0 D 0 ,
которое означает, что точка (x0 , y0 , z0 ) прямой L принадлежит плоскости П
, то прямая лежит в этой плоскости. Таким образом, принадлежность прямой, заданной каноническими уравнениями (13.2), плоскости П : Ax By Cz D 0 определяется выполнением условий
Am Bn Cp 0
Ax0 By0 Cz0 D 0 .
Если прямая L задана как линия пересечения двух плоскостей
A1x B1 y C1z D1 0
A2 x B2 y C2 z D2 0 ,
то ее направляющий вектор может быть получен как векторное произведение нормальных векторов этих плоскостей (см. рис. 12.3), т.е.
SN1 N2 ,
изадача нахождения угла между прямой иплоскостью сводится к
предыдущей. В этом случае
N1 N2 , N |
|
(N1, N2 , N ) |
|
|
|
|
|
|
|
sin | N1 N2 | | N | |
|
|
|
. |
|
|
|
|
|
| N1 N2 |
| | N | |
|
|
|
|||||
13.3.Пересечение прямой с плоскостью. Вычислим теперь |
|||||||||
координаты точки пересечения прямой L : |
x x0 |
|
|
y y0 |
|
z z0 |
и |
||
m |
|
n |
p |
||||||
|
|
|
|
|
|
|
|||
плоскости П : Ax By Cz D 0 при условии, что они пересекаются. Перейдём от канонических уравнений прямой к параметрическим
x x0 |
|
y y0 |
|
z z0 |
|
m |
n |
p |
|||
|
|
x mt x0
t y nt y0z pt z0
Найдем значение параметра t1 , при котором соответствующая точка прямой принадлежит плоскости, т.е. удовлетворяет уравнению
A mt x0 B nt y0 C pt z0 D 0
или, что тоже,
96
( Am Bn Cp)t ( Ax0 By0 Cz0 D) . |
(13.2) |
Если Am Bn Cp 0 и Ax0 By0 Cz0 D 0 , то это уравнение не имеет
решений. Эти условия соответствуют тому, как мы выяснили выше, что прямая и плоскость параллельны и, следовательно, не пересекаются. Если Am Bn Cp 0 и Ax0 By0 Cz0 D 0 , то уравнение (13.2) имеет
бесчисленное множество решений, т.е. прямая принадлежит плоскости. И, наконец, если Am Bn Cp 0 , то
t1 |
|
Ax0 By0 |
Cz0 |
D |
. |
|
Am Bn Cp |
||||||
|
|
|
||||
Подставим это значение в параметрические уравнения прямой и найдем x1, y1, z1 – координаты точки пересечения прямой L с плоскостью П .
Если прямая L задана как линия пересечения двух плоскостей
A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0 ,
а плоскость задана уравнением Ax By Cz D 0 , то координаты точки
их пересечения находим, решая следующую систему трех линейных уравнений:
Ax By Cz D 0 |
||||
|
A1x B1 y C1z D1 0 . |
|||
|
||||
A x B y C z D 0 |
||||
|
2 |
2 |
2 |
2 |
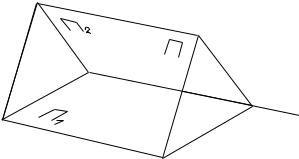
Здесь возможны варианты. Если определитель матрицы этой системы не равен нулю, то искомая точка пересечения единственна и находится, например, по правилу Крамера. Если определитель матрицы этой системы равен нулю, что означает компланарность нормальных векторов к этим плоскостям, то система может быть несовместна (см., например, рис. 13.3)
97
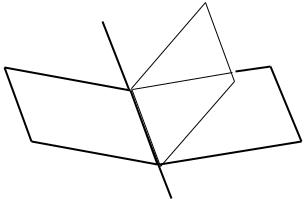
Рис. 13.3
или иметь бесчисленное множество решений, когда эти три плоскости пересекаются по одной прямой(см. рис. 13.4).
Рис. 13.4
Лекция 14. Другие задачи о прямых и плоскостях
Рассмотрим несколько типичных задач получения уравнений прямых или плоскостей, обладающих заданными свойствами.
Задача 1. Составить уравнения прямой L , проходящей через данную точку M x0 , y0 , z0 перпендикулярно к данной плоскости П : Ax By Cz D 0
.
98

= { , , }
0 0, 0, 0
L 
Рис. 14.1
Очевидно, что в качестве направляющего вектора прямой можно взять нормальный вектор к плоскости, т.е. S N {A, B,C}. Отсюда следует, что уравнения искомой прямой имеют вид
x x0 |
|
y y0 |
|
z z0 |
. |
(14.1) |
|
|
|
||||
A |
|
B |
|
C |
|
|
Задача 2. Составить уравнение плоскости П , проходящей через данную точку M1 (x1, y1, z1 ) перпендикулярно к данной прямой L
x x0 |
|
y y0 |
|
z z0 |
. |
|
|
|
|||
m |
|
n |
|
p |
|
Очевидно (см. рис. 14.2), что в качестве нормального вектора плоскости можно взять направляющий вектор прямой, т.е. N s m, n, p
. Отсюда следует, что уравнения искомой плоскости имеет вид
m x x1 n y y1 p z z1 0. |
(14.2) |
П
Рис. 14.2
99
