Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

10261

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

4.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

a12 4a0 a2 0 ,	1	2 ,		a1		y C1 e 1 x C2e 2x .
a12 4a0 a2 0 ,	1	2			,	y (C1 C2 x)e 1 x .

				2a0
a12 4a0 a2 0 ,	1,2		i ,			y e x(C1 cos x C2sin x) .
a0 y a1 y a2 y q(x)	(a0 0) .

y Y y ,

Y – y –

y1 (x) y2 (x) –

a0 y a1y a2 y 0

C1 (x) C2 (x)

C	(x) y (x) C		(x) y	2	(x) 0,
1	1	2		2
			(x) y		(x) q(x)
C1	(x) y1	(x) C2	(x) y	2	(x) q(x)
	q(x)				).

a0 y a1 y a2 y 0 ,

				-

	y1		,	y C1 (x) y1 (x) C2 (x) y2 (x) –

y		const
2

a0 y a1 y a2 y q(x) .

(

a0 y a1y a2 y Pn (x) e x ,	Pn (x) –	-
n, –	,	-

			y Q (x) e x xm ,
Qn (x) –	n		n		-
Qn (x) –	n				-
, m –			a0	2 a1	a2 0 ,
		.
a0 y a1 y a2 y e x Pn (x) cos		x Qk (x) sin x ,			Pn (x)
Qk (x) –	n k, i –				-
,					-
y e x M (x) cos	x N (x) sin		x xm ,	M (x)	N(x)
–		n	k, m –		-
,		n	k, m –		-
,
i .

a0 y a1 y a2 y q1(x) q2 (x)

a0 y a1 y a2 y q1(x)

a0 y a1 y a2 y q2 (x).

9.1.

Y –

, X

B»

m+n

(A, B)

m n

(

–

)

(

)

: =(a1, a2, , ak).

–

nk.

k = 0

n0 = 1 –

–

Pn 1 2 3 n n!

n (n 1) (n 2) (n (k 1))

(n k)!

–

Cnk

n (n

1) (n 2) (n (k

1))

(n k)! k!

(a b)n Cn0anb0 Cn1`an 1b1 Cn2 an 2b2 Cnn a0bn Cnk a

k 0

(

: {1,1,2,5} –

CPk ,

: Ckn Ckn k 1 .

	-
	,
m	-
n	-
.
	-
	k
	k
2n.	.
	.
	-

n k bk .

							{1,2, , n}	1
k1			,			2 k2 , ,	n kn ,	-
			k=k1+k2+ +kn.
			k!			.
	k !k	2	! k	n	!	.
1		2		n

9.2.

							A, B,..., X, Y,
... .							a, b,..., x, y, ...
	x X		,	x			X, -
	x X –	x				X.
	X	Y	.		(X = Y),		-
	X		.		Y (	Y ),
	X				Y (	Y ),
	X				Y.
X	Y	Y,		X	Y.		Y
	Y	Y,		X			Y
(	Y).
	X	Y		X Y (X Y		(	)
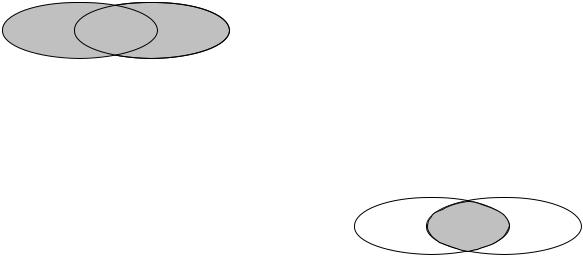
				X Y (X Y		X+Y)	-
				,		X
					Y (	X
	. 9.1.				Y (	. 9.1).
			:
		X Y = Y X,
		(X Y) Z = X (Y Z) = X Y Z.
		(		)		X	Y
	X Y (X Y		X Y)	-		X	Y
	X Y (X Y		X Y)	-
	,	,
	X,	,		Y
	X,			Y	. 9.2.
(	. 9.2).		:		. 9.2.
			:
		X Y = Y X,
		(X Y) Z = X (Y Z) = X Y Z.
			:
	(X Y) Z = (X Z) (Y Z)			(X Y) Z = (X Z) (Y Z).

(

X = X, X = .

(

)

(

)

(

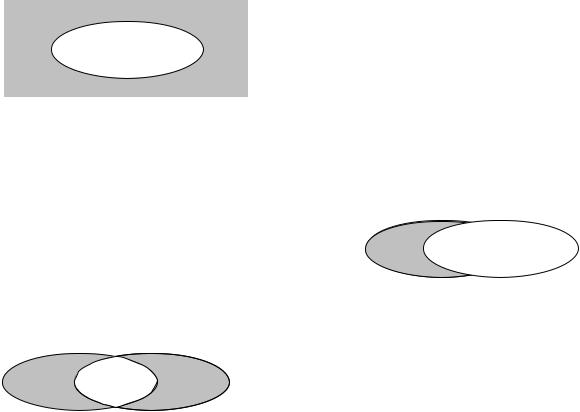
: X = , X = X.

X (

X )

X (

. 9.3).

. 9.3.

X ,

I, X

X Y

X \ Y)

X Y (

Y (

. 9.4).

X Y

Y :

X \ Y X

. 9.4.

(

. 9.5):

. 9.5.

X Y = (X Y) \ (X Y)

X Y = (X \ Y) (Y \ X ).

9.3.

	–						,			-
(	),	(			).
	.				(	)			,	-
	.	0,				1.			,	-
		0,				1.
a )		,			a (	a.
a )		,				a.		a	a
	:			a	(	-		0	1
	:		a	a	(	-		0	1
).								1	0
).

		(	disjunctio –	,	)
		a b (	: a b, a + b)		-
,	“a	b“,	,
		,		.
		:
		a b b a ,

a (b c) (a b) c = a b c .

		(	conjunctio –		,	)	-
	a	b	,		“a	b”,
a b)	,		a	b (		:	a b,
a b)	,		:		.
			:

a b b a ,

a (b c) (a b) c = a b c .

(a b) c (a c) (b c)									(a b) c (a c) (b c)
			:			a			,			a				.
				a b						a b
				a b				b		a b					b
	(								implicatio –								)			-
a	b									,						“	a,			b”
”a	b”,												,				a –			, b –
,						–				(							a b).			-
												: (a b) (a							) .
												: (a b) (a						b	) .
			a		b					(				.			a b),
a b b	a.		a		b					(							a b),
a b b	a.																			.
										:										.
										:
		a	b		a b		a b				a b		a b
		1	1		1		1				1			1
		1	0		1		0				0			0
		0	1		1		0				1			0
		0	0		0		0				1			1

9.4.

,	–	,		-
,		,
.			a,b
e	a	b	a,b	-
(	a –	,	b –	),
	.		a,b	-

			,											,				–
			(a		b		b				a).							-
											,							-
	.		.									,						-
			.
			(				)				,							-
	.										,			.				-
	.		a,a ,								a			.		,		-
			a,a ,								a					,		-
			.		:							G V , E, I ,					V
–			, I –		:					E		G V , E, I ,					V
–			, I –							E
			V.					V								,		-
			E –		,		I –								.
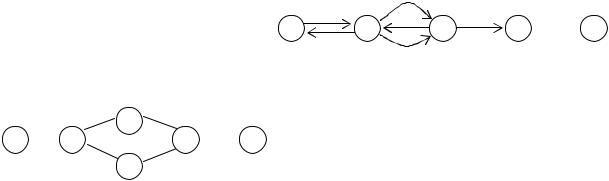
			: V 1,2,3,4,5 ,		E a,b,c,d,e, f ,								I					:

					a		b		c		d		e		f
				(1,2)		(2,3)			(3,4)		(2,1)		(2,3)		(3,2)
					-				a		b
	,				-		1		a	2	f	3		c	4			5
	,			.	9.6.		1		d	2		3			4			5
											e

			5		-
	.		5		-							. 9.6
	.											. 9.6
			1															-
2		3	6		4													-
2		3	6		4			.										-
			5					.										-
			5												,			-
			. 9.7								6					5		.
			. 9.7								6					5
(	. 9.7)		V={1,2,3,4,5,6},						E 1,3 , 1,6 , 2,3 , 3,5 , 5,6 ,									-
	4		–			.								,
			–											,	.
			,												.			-
			,															-
	,		–	.										.
											;			.
	,									.	;
	,							.		.								-
								.										-
								,								–		-

.				,
.
–		,			.
,				.
–			.
(				)	.
5				9.8	1,2 ,
5	5,1	–		,	1,4 , 1,3
4		.
1		.	:
1			:
3		2,3,5,4	–	;	;
2		2,3,4,5,1,3,4–		,	;
. 9.8		3,1,4,5,1,2–		,	;
. 9.8		1,3,4,1,2,3,1–			,
		1,3,4,1,2,3,1–			,
1,2,3,1,4,5,1–		,		;
2,3,4,5,1,2 –			.		,
		.			,
		.			1
		,			-
			.		-
			.
			.
,			,		.
	. 9.9,			1 –	,
,			: 1,2,5; 1,5; 1,3,4,5.

2,3 , 3,4 , 4,5 ,

– -

;

	2
		5
3	4
	. 9.9
,	,	-
	5 –	-

10.

10.1.

						-
;			,	,	,	( -
,	)	. .;			;
					;
		-			-
;		-			.
					,	-
.						-

,	(	)	,
(	),
	.

)		,	.			(			-
)			.	,
				,
		.							-
		.	M
.	x,y M		M	z=x y,			z M, . .
.	x,y M			z=x y,			z M, . .
M			.				x,y M
	x y=y x.		,				x,y M		-
e M	x y=y x.								-
e M		x M					x e=x		-
,		x M					x e=x
e x =x.						0.
						0.
		x M				1.			-
		x M							-
x M,	x x =e	x x=e (							-
e	).	,	e=0,					x	-
–x.		,	e=0,					x	-
–x.		,	e=1,						x
x–1 (x=0		,	e=1,				M).		x
x–1 (x=0							M).
	(x y) z=x (y z).		,			x,y,z M			-
	(x y) z=x (y z).		.
			.

	,			,			a	b
	,			,	a		a	b
	x,		,	-	a		a	b
y,	x,	x y.	,	-	b		a	b
				-	b		a	b
	M={a,b}.			-
	M={a,b}.
,			"	"		,			-
			(						-
).									-
). a, b		(							-
). a, b				,					-
.	M								-
	M								-

G (G=(M, )),

	, . .				(x y) z=x (y z)
x,y,z M;
	M				e	,
x M	x M			x e=x e x =x;		x M	,
	x M					x M	,
x x =e	x x =e.				,	G=(M, )		-
					,	G=(M, )		-
	(			).	:
N –		, Z –		, Q –	:	, R –		,
N –		, Z –		, Q –		, R –		,
C –	.			: (Z, +), (Q, +), (R, +), (C, +).
				: (Z, +), (Q, +), (R, +), (C, +).
	,				–	0,
x					–x.
(R , C ) –				: (Q , ), (R , ), (C , ).				Q
(R , C ) –	.			(		,	)	,
	.
G=(M, ).	G'=(M',		),	M' M,
G=(M, ).				(Z, +) (Q, +) (R, +) (C, +).
				(Z, +) (Q, +) (R, +) (C, +).
				(Q , ) (R , ) (C , ).
	G1=(M1, )		G2=(M2, ) –
			.	G1=(M1, )	G2=(M2, )		,
					:M1 M2,
	x,y M1			(x y)= (x) ( y).		: G1 G2.
			: (R+, ) (R, +),			: G1 G2.
			: (R+, ) (R, +),			: R+ R
	(x)=ln x.			ln (x y)= ln (x)+ln (y) ,			.
	–						,	-
	K=(M, +,	).			(+)		( ).	-
:	K=(M, +,	).
:			:	(M, +)
	,		:	(M, +)		.
	,			0,	,	.	x,	-
	–x;			0,	,		x,	-
	–x;					,		-
						,	.	-
				,			.	,
				,				,
				,			;

x (y+z)=(x y)+(x z)	(y+z) x=(y x)+(z x).		:
x (y+z)=(x y)+(x z)	(y+z) x=(y x)+(z x).
K'=(M', +, ),		M' M,	K=(M, +, ).
	(Z, +, ) (Q, +, ) (R, +, ) (C, +, ),
		.
		F=(M, +, ),	:
			,	-
		1,	,	x
		,	x–1;	,
				,
. . 0 1.		,		;
x–1		x 0.
(M*, )			.
,		M' M,	.
F'=(M', +, ),		M' M,	F=(M, +, ).
			:

(Q, +, ) (R, +, ) (C, +, ).

10.2.

	–		,		-
,	.			.
,			.	.
			.
		V,
		,			.
,			,		-
,		.	,
		.			-
		.			-
	x	.		e1, e2, … , en
	x			e1, e2, … , en
		x = x1 e1 + x2 e2 + … + xn en,
	x1, x2, … , xn			x	-
e1, e2, … , en,					x
e1, e2, … , en.		x	V		-
	(x)	x	V		-
	(x)		,	,	-
	.	(x)		x	-
,	x			(x).

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20234.69 Mб010257.pdf
#
25.11.20234.69 Mб010258.pdf
#
25.11.20234.69 Mб010259.pdf
#
21.11.2023170.87 Кб01026.pdf
#
25.11.20234.69 Mб110260.pdf
#
25.11.20234.69 Mб010261.pdf
#
25.11.20234.69 Mб010262.pdf
#
25.11.20234.69 Mб010263.pdf
#
25.11.20234.69 Mб010264.pdf
#
25.11.20234.69 Mб010265.pdf
#
25.11.20234.69 Mб010266.pdf

	–						,			-
(	),	(			).
	.				(	)			,	-
	.	0,				1.			,	-
		0,				1.
a )		,			a (	a.
a )		,				a.		a	a
	:			a	(	-		0	1
	:		a	a	(	-		0	1
).								1	0
).

	–						,			-
(	),	(			).
	.				(	)			,	-
	.	0,				1.			,	-
		0,				1.
a )		,			a (	a.
a )		,				a.		a	a
	:			a	(	-		0	1
	:		a	a	(	-		0	1
).								1	0
).

	–						,			-
(	),	(			).
	.				(	)			,	-
	.	0,				1.			,	-
		0,				1.
a )		,			a (	a.
a )		,				a.		a	a
	:			a	(	-		0	1
	:		a	a	(	-		0	1
).								1	0
).