
10169
.pdf
50
сопротивления в форме: M × &y& + C × y = 0 или, разделив левую и правую части
уравнения на M и обозначив через |
ω 2 = |
С |
, |
окончательно получим: |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
&& |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ω × y = 0 . |
|
|
|
|
|
|
|
(5.2) |
|||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||
В (5.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = |
C |
= |
|
1 |
|
|
= |
|
|
Q |
= |
|
g |
(5.3) |
||||||||
|
|
|
|
|
|
M × yст |
|
|
|
|
|||||||||||||
|
|
|
M |
|
δ × M |
|
|
|
|
yст |
|
|
|||||||||||
- круговая или циклическая частота свободных колебаний или число колебаний
за время (2 ×π ) |
секунд. Здесь δ - перемещение точки приложения груза (массы) |
|||||
от действия единичной силы |
|
= 1. |
|
|||
P |
|
|||||
Составим |
|
характеристическое уравнение |
r 2 + ω 2 × y = 0 . Его решением |
|||
будет: r1,2 = ±ω × |
|
|
= ± i ω . Каждому корню rk |
|
||
|
-1 |
характеристического уравнения |
||||
будет соответствовать решение дифференциального уравнения в виде Ck × erk ×t , то есть:
y = C1 × eiω t + C2 × e -iω t , |
(5.4) |
где С1 и С2 – произвольные постоянные, которые можно определить из
начальных условий t0 , y0 , y0 |
= V0 . |
|
|
|
|
|
|
& |
|
|
|
|
|
Решение (5.4) преобразуем, используя формулу Эйлера: |
|
|
|
|||
|
|
e± iω t = cosω t ± i sin ω t . |
|
|
|
|
Тогда: |
y = C1 (cosω t + i sin ω t) + C2 (cosω t - i sin ω t) = |
|
|
|
||
|
= i (C1 - C2 ) ×sin ω t + (C1 + C2 ) × cosω t . |
(5.5) |
||||
|
a1 = i (C1 - C2 ); |
b1 = C1 + C2 - |
|
i = |
|
. |
Обозначим: |
произвольные постоянные; |
-1 |
||||
Тогда выражение (5.5) примет вид: |
|
|
|
|
||
|
|
y = a1 × sin ω t + b1 × cosω t . |
(5.6) |
|
||
Введем другие произвольные постоянные: |
|
|
|
|||
|
|
a1 = A × cosα , |
b1 = A ×sin α . |
|
|
|
Подставив в (5.6) получим: y = A × (sin ω t × cosα + cosω t × sin α ) , или окончательно:
y = A × sin (ω t + α ) |
(5.7) |
|
|
|
|
Получено решение дифференциального уравнения свободных колебаний системы с одной степенью свободы, которые будут происходить по гармоническому закону с амплитудой колебаний A , начальной фазой α и
|
51 |
|
|
|
|
|
ω = |
|
= |
|
[ рад/ с] . Поскольку ω |
частотой собственных колебаний |
C / M |
1/(M ×δ11 ) |
|||
показывает число колебаний за |
время 2π |
сек, она называется круговой |
|||
собственной частотой колебаний. Она не зависит от начальных условий и является динамической характеристикой при колебаниях системы с одной
степенью свободы. Способ ее определения рассмотрим на примере. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
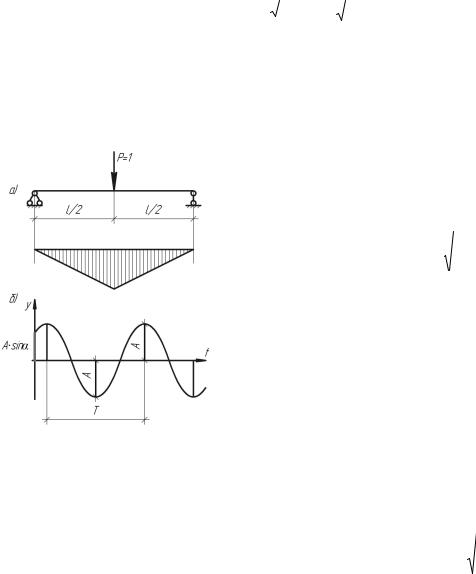
Пример. Рассмотрим колебания упругой |
|||||||||||||||||||||||||||
|
|
|
|
|
|
системы |
|
с |
|
одной |
степенью |
свободы |
по |
||||||||||||||||||||
|
|
|
|
|
|
рис.5.2а. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
δ11 = |
|
|
, ω = |
48 × E × I |
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 × E × I |
M × l 3 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
На рис. 5.2б показан график гармонических |
|||||||||||||||||||||||||||
|
|
|
|
|
|
колебаний |
|
системы: |
T = |
2 ×π |
(сек) |
- |
|
|
|
период |
|||||||||||||||||
|
|
|
|
|
|
|
ω |
||||||||||||||||||||||||||
|
|
|
|
|
|
собственных колебаний, т.е. время одного |
|||||||||||||||||||||||||||
|
|
|
|
|
|
полного колебания системы. Величины A |
и |
||||||||||||||||||||||||||
|
|
|
|
|
|
α |
в (5.7) |
определяем из начальных условий: |
|||||||||||||||||||||||||
Рис. 5.2 |
|
|
при t |
= 0, |
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y0 , y0 = V0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
||
y = A × sin α ; |
sin α = |
; y0 |
= A ×ω × cos(ω t |
+ α ) = A ×ω × cosα ; |
cosα = |
|
|
y0 |
; |
||||||||||||||||||||||||
A |
|
A ×ω |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
×ω |
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|||||
α = arctg |
|
0 |
. sin 2 α + cos2 α = |
|
0 |
|
+ |
|
|
|
0 |
|
|
= 1, тогда A = |
y02 + |
|
|
0 |
. |
|
|
||||||||||||
|
y0 |
|
2 |
|
A |
2 |
|
2 |
|
|
|
ω |
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
×ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.Свободные колебания системы с конечным числом
степеней свободы без учета сил сопротивления
Свободные колебания системы вызываются начальными возмущениями.
Они происходят только под действием внутренних сил. В процессе исследования свободных колебаний определяют частоты и формы собственных колебаний,
необходимые для динамического расчета конструкций.
Собственными называются свободные колебания по одной из собственных форм. Собственная форма - это форма свободных колебаний системы,
совершающихся по гармоническому закону с одной и той же частотой.
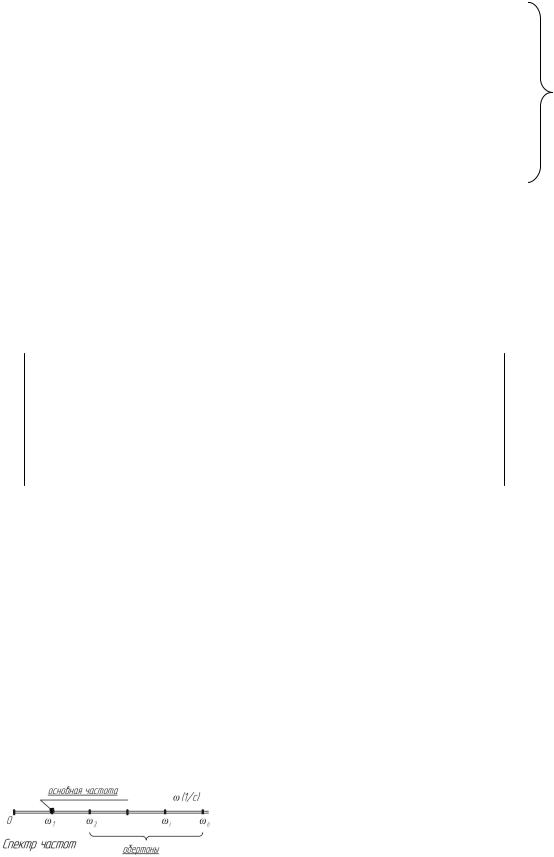
Рассмотрим собственные поперечные колебания балки, несущей n
точечных масс (рис. 6.1).В момент времени t положение масс системы будет

52
определяться ординатами
y1 , y2 , . . . , yi , . . . , yn .
F |
, F |
, . . . , F , . . . , |
и1 |
и2 |
Рисi . 6.1 |
Представим отклонение центра каждой массы системы как результат действия системы сил инерции
Fиn , где: Fиi |
= -M i × yi , т.е.: |
|
&& |
|
y1 = Fи1 ×δ11 + Fи2 ×δ12 + ... + Fиi ×δ1i + ... + Fиn ×δ1n ; |
|
y2 = Fи1 ×δ 21 + Fи2 ×δ 22 + ... + Fиi ×δ 2i + ... + Fиn ×δ 2 n ; |
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (6.1) |
|
yi = Fи1 ×δ i1 + Fи2 ×δ i 2 + ... + Fиi ×δ ii + ... + Fиn ×δ in ; |
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
|
yn = Fи1 ×δ n1 + Fи2 ×δ n 2 + ... + Fиi ×δ ni + ... + Fиn ×δ nn . |
При составлении уравнений (6.1) в этом случае использован метод сил.
Подставим выражение каждой силы инерции Fиi |
= -M i |
× yi в формулу (6.1) и |
|
|
&& |
перенесем все члены полученной системы уравнений в одну сторону. Тогда дифференциальные уравнения свободных колебаний системы с “n” степенями свободы без учета сил неупругого сопротивления и с начальными условиями: при
t = 0, y0i |
, y |
0i (i = 1, 2, ..., n) , примут вид: |
|
|
|
|
|
|||||
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
+ M 1 |
× y1 ×δ11 |
+ M 2 |
× y2 |
×δ12 |
+ ... + M i |
× yi |
×δ1i + ... + M n × yn ×δ1n = 0 ; |
||
|
|
y2 |
+ M 1 |
&& |
+ M 2 |
&& |
×δ 22 |
+ + M i |
&& |
×δ 2i |
+ + M n |
&& |
|
|
× y1 ×δ 21 |
× y2 |
× yi |
× yn ×δ 2 n = 0 ; |
|||||||
|
|
|
|
&& |
|
&& |
|
|
&& |
|
|
&& |
|
|
y. i. |
+. .M. 1. |
×.y.1 .×δ. .i1 . |
+. M. .2. |
×.y.2 . |
. . . |
. . . . . . . |
. . . |
. . . |
. . . . . . . |
. . . . . . . . . . (6.2) |
|
|
×δ i 2 + ... + M i × yi ×δ ii + ... + M n × yn ×δ in = 0 ; |
||||||||||
|
|
|
|
&& |
|
&& |
|
|
&& |
|
|
&& |
|
|
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
||||||||||
|
|
yn |
+ M 1 |
× y1 ×δ n1 |
+ M 2 |
× y2 |
×δ n 2 |
+ ... + M i |
× yi |
×δ ni |
+ ... + M n |
× yn ×δ nn = 0 . |
|
|
|
|
&& |
|
&& |
|
|
&& |
|
|
&& |
Решение системы уравнений (6.2) представляют в виде гармонических колебаний:
yi = Ai × sin (ω t + α ) , (i = 1, 2, ..., n) |
(6.3) |
|
|
|
|
с амплитудой A , собственной круговой частотой ω и начальной фазой α . При этом полагают, что все отклонения происходят в одной фазе. Подставив это
решение в систему дифференциальных уравнений (6.2), |
после преобразований |
|||
(сокращения на sin (ω t + α ) ), сгруппировав все члены с |
y |
i |
и поделив на ω 2 |
, |
|
|
|
|
|
53
получим систему линейных однородных алгебраических уравнений относительно
амплитуд колебаний A1 , A2 ,..., Ai |
,..., An |
( |
y = Ai ×ω |
2 |
× sin (ω t + α ) ) : |
|||||||||||
|
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
|
(M 1 ×δ11 |
- |
1 |
) × A1 + M |
2 ×δ12 × A2 +...+ M i ×δ1i × Ai + ...+ M n ×δ1n × An = 0 ; |
||||||||||||
|
||||||||||||||||
|
|
ω 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
M 1 ×δ 21 |
× A1 + (M 2 ×δ 22 |
- |
1 |
) A2 +...+ M i ×δ 2i × Ai + ...+ M n ×δ 2n × An = 0 ; |
||||||||||||
ω 2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(6.4) |
||||
. . . . . . |
. . |
. . |
. . . . .. . . |
. |
.. . |
. . . . |
. . |
. . . . |
. |
. |
. |
|
||||
M 1 ×δ i1 × A1 + M 2 ×δ i 2 × A2 |
+...+ (M i |
×δ ii - |
|
1 |
) × Ai + + M n ×δ in × An = 0 ;... |
|||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
ω 2 |
|
|
|
|
|||
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
||||||||||||||||
M 1 ×δ n1 × A1 + M 2 ×δ n2 × A2 |
+...+ M i ×δ ni × Ai |
...+ + (M n ×δ nn - |
1 |
) × An = 0 . |
||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω 2 |
||
Система (6.4) допускает два вида решений: |
|
|
|
|||||||||||||
- нулевое, |
когда A1 = A2 = ... |
= Ai |
= ... |
= An |
= 0 , т.е. движение отсутствует; |
|||||||||||
- отличное от нуля, которое возможно в том случае, когда определитель системы уравнений, составленный из коэффициентов при неизвестных амплитуд,
равен нулю:
(M 1 ×δ11 - λ) |
M 2 ×δ12 |
. . . |
M i ×δ1i |
. . . |
M n ×δ1n |
M 1 ×δ 21 |
(M 2 ×δ 22 - λ) |
. . . |
M i ×δ 2i |
. . . |
M n ×δ 2n |
. . . . . . . . . . . . . . . . |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = 0, (6.5) |
M 1 ×δ i1 |
M 2 ×δ i 2 . . . (M i ×δ ii - λ) . . . M n ×δ in |
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
M 1 ×δ n1 |
|
|
M 2 ×δ n 2 . . . |
M i ×δ ni |
. . . (M n ×δ nn - λ) |
|
где обозначено |
λ = |
1 |
|
- величина обратная квадрату круговой собственной |
||
ω 2 |
|
|||||
|
|
|
|
|
|
|
частоты колебаний. |
|
|
|
|
||
Выражение |
(6.5), |
|
являющееся алгебраическим уравнением n − ой степени |
|||
относительно ω 2 |
(или |
|
λ) , называют уравнением частот или вековым |
|||
уравнением, позволяющим определить собственные частоты. Решение этого уравнения дает столько значений собственных частот, сколько степеней свободы
имеет система. Их |
располагают в убывающем порядке λ1 |
F λ2 F ... F λi |
F ... F λn , |
||
что соответствует |
ряду значений собственных |
частот |
|
ω1 P ω2 P ... P ωi P ωn , |
|
|
(рис. 6.2). Наименьшая частота называется |
||||
|
основной частотой, |
а |
другие частоты - |
||
|
обертонами. |
Вся |
совокупность |
частот |
|
Рис. 6.2 |
собственных колебаний системы называется |
||||
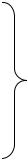
|
54 |
|
спектром ее собственных частот. Каждой частоте |
ωk соответствует |
|
собственное колебание |
yik = Aik × sin(ωk t + α k ), (i = 1, 2, ..., n) . |
Для формирования |
уравнения частот (6.5) |
необходимо вычислить удельные перемещения δ ij по |
|
известным методам строительной механики, построив предварительно эпюры
изгибающих моментов от действия единичных сил |
Pi |
= 1 , |
(i = 1, 2, |
... , n) , |
|||
приложенных по направлению соответствующих координат |
yi |
(i = 1, 2, ..., n). |
|
||||
6.1. Формы собственных колебаний |
|
|
|
|
|
||
Общее решение (6.3) |
содержит |
n2 |
неизвестных |
амплитуд A |
и n |
||
|
|
|
|
|
|
ik |
|
начальных фаз, то есть всего |
(n2 + n) произвольных постоянных, |
в то время как |
|||||
число начальных условий: при |
t = 0 , y0i , |
y0i |
(i = 1, 2, ... , n ) |
- равно только |
(2 × n) . |
||
|
|
& |
|
|
|
|
|
В связи с этим необходимо уменьшение числа произвольных постоянных.
Поскольку из уравнений (6.4) непосредственно определить амплитуды колебаний
не удается, |
то |
выражают отношения |
амплитуд |
ρik |
= |
Aik |
, |
называемые |
|
|
|||||||||
|
|
|
|
|
|
|
A1k |
|
|
коэффициентами |
форм колебаний |
или относительными |
амплитудами |
||||||
свободных |
колебаний системы. |
Они |
характеризуют |
собственные формы |
|||||
колебаний, выражая все координаты системы через одну произвольную,
определяющую колебания в принятом направлении y1 .
Коэффициенты форм колебаний могут быть определены из уравнения амплитуд (6.4). С этой целью поделим все члены уравнения амплитуд на A1k и,
подставляя поочередно в эти уравнения значения частот, получим систему уравнений для определения коэффициентов форм колебаний:
(M 1 ×δ11 |
- |
1 |
) × |
A1k |
+ M |
2 ×δ12 |
× |
|
A2k |
|
+...+ M i ×δ1i |
× |
Aik |
+ ...+ M n |
×δ1n |
× |
Ank |
= 0 ; |
||||||||||||||
ω 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
A |
|
|
|
A |
|
|
|
A |
|
||||||||||
|
|
|
|
|
|
k |
|
1k |
|
|
|
|
|
|
1k |
|
|
|
|
1k |
|
|
|
|
1k |
|
||||||
M 1 |
×δ 21 |
× |
A1k |
+ (M 2 ×δ 22 |
- |
1 |
) × |
A2k |
+...+ M i ×δ 2i |
× |
Aik |
+ ...+ M n |
×δ 2n |
× |
Ank |
= 0 ; |
||||||||||||||||
|
|
|
|
A |
||||||||||||||||||||||||||||
|
|
|
|
A |
|
|
|
|
|
ω |
2 |
|
|
|
A |
|
|
|
|
A |
|
|
|
|
|
|||||||
|
|
|
|
|
1k |
|
|
|
|
|
k |
|
|
|
1k |
|
|
|
|
1k |
|
|
|
|
1k |
|
||||||
. . . |
×.δ.n.1 |
.× A. . . |
+. M 2 ×δ n 2 ×. . . .. . . . |
.. |
. |
.+.....+ M i ×δ ni ×. . . . . . . . |
. . . |
+. ....+ (M n ×δ nn -. . . . . . . . . . .ω 2. . |
). × A. . . |
(6.6) |
||||||||||||||||||||||
M 1 |
A |
A |
= 0 . |
|||||||||||||||||||||||||||||
|
|
|
|
A1k |
|
|
|
|
A2k |
|
|
|
|
|
|
|
Aik |
|
|
|
|
|
|
1 |
|
|
|
Ank |
|
|||
|
|
|
|
1k |
|
|
|
|
|
1k |
|
|
|
|
|
|
|
1k |
|
|
|
|
|
|
k |
|
|
|
1k |
|
||
или в общем виде:

55
n |
|
yi = ∑ ρik × A1k × sin (ωk t + α k ), (i = 1, 2, ... , n) . |
(6.7) |
k =1
Свободные колебания происходят, таким образом, по этому сложному закону и состоят из суммы гармонических собственных колебаний системы. В
этом решении неизвестных ρik равно n, неизвестных α k - то же n, т.е. общее
число неизвестных произвольных постоянных – 2n, что соответствует количеству
начальных условий. Собственные частоты ωk и коэффициенты ρik не зависят от
начальных условий и являются динамическими характеристиками системы с
“ n ” степенями свободы.
Собственные формы колебаний системы как и коэффициенты форм колебаний обладают свойством ортогональности, то есть удовлетворяют
условию:
n |
|
∑ M i × ρik × ρij = 0 . (k ¹ j ) |
(6.9) |
i=1
Коэффициенты форм колебаний позволяют построить собственные формы колебаний. При их построении пренебрегают продольными деформациями стержней по сравнению с изгибными деформациями и угловыми деформациями жестких узлов. Вычислив коэффициенты форм, выражают амплитуды колебаний для каждой собственной формы:
Aik = ρik × A1k , |
(i = 1, 2, ... , n ) |
(6.10) |
|
|
|
|
|
ивыполняют построение форм колебаний.
7.Свободные колебания системы с одной степенью свободы с учетом сопротивления среды
При свободных колебаниях сооружений с течением времени наблюдается их затухание. Это связано с действием на сооружение сил сопротивления,
направления которых противоположны скорости движения системы.
В динамических расчетах учитывают следующие силы сопротивления:
- аэродинамические силы сопротивления, возникающие вследствие воздействий на сооружение или конструкцию внешней среды – воздуха, воды и др. Эта сила сопротивления зависит от скорости колебаний: R1 = -b1 ×V - при небольших колебаниях; R2 = -b2 ×V 2 - при больших скоростях колебаний. Здесь b1
56
и b2 - коэффициенты, характеризующие вязкость среды и аэродинамические
характеристики сооружений;
-сухое или кулоново трение, характеризующее трение между твердыми телами (например, в опорных закреплениях конструкций зданий и сооружений);
-силы неупругого сопротивления или внутреннего трения, являющиеся наиболее значимыми при рассмотрении колебаний упругих систем. Эти силы возникают за счет неидеальных упругих свойств материалов строительных конструкций, т.е. за счет поглощения материалом конструкций части энергии колебаний и последующим выделением этой части энергии, например, в виде тепла. Величина этого поглощения энергии характеризуется коэффициентом
поглощения ψ = - W , где: W - энергия колебаний за период T1 ; |
W - часть |
||||||||||
W |
|
|
|
|
|
|
|
|
|
|
|
энергии, поглощенная материалом конструкции за время T1. |
|
|
|||||||||
ψ = - DW = - |
t +T1 |
dW |
|
|
|
|
|
|
+T1 = |
||
∫ |
= - |
|
lnW |
|
tt |
||||||
|
|
||||||||||
|
|||||||||||
W |
t |
W |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
= lnW (t) - lnW (t + T1 ) = ln |
|
|
|
W (t) |
|||||||
|
|
. |
|||||||||
|
|
||||||||||
|
|
|
|
|
W (t + T1 ) |
||||||
Рис. 7.1
Выразим энергию колебаний W = E + П как сумму кинетической и потенциальной энергий. Так как в начале и окончании периода собственных колебаний скорости колебаний отсутствуют, то E = 0. В эти же моменты времени
Wmax = П . |
|
|
|
||
W (t) = |
1 |
× C × yn2 ; |
W (t + T1 ) = |
1 |
× C × y |
|
|
||||
2 |
|
2 |
|
||
2 |
|
ψ = ln |
(1/ 2) × C × yn2 |
yn |
|
|
n+1 |
; |
|
= 2 × ln |
|
. |
|
2 |
yn+1 |
|||||
|
|
|
(1/ 2) ×C × yn+1 |
|
||
Величину ln yn = δ называют логарифмический декремент затухания. yn+1
Таким образом, коэффициент поглощения энергии колебаний ψ = 2 ×δ .
При динамических расчетах строительных конструкций затухание колебаний принято характеризовать коэффициентом неупругого сопротивления
материала |
γ = |
ψ |
= |
δ |
. Он зависит от свойств материала конструкции и |
|
2 ×π |
π |
|||||
|
|
|
|
|||
составляет: |
|
|
|
|
|
|
|
|
57 |
- |
для железобетона: |
γ жб = 0,1; |
|
- |
для стали: |
γ сталь |
= 0,025 ; |
- |
для дерева: |
γ дер. |
= 0,05 ; |
- |
для кирпичной кладки: |
γ жб = 0,08 . |
|
Дифференциальное уравнение движения системы с одной степенью свободы с учетом сил сопротивления было получено в п.5 (см. формулу 5.1) и
имеет вид:
|
|
M × y + b × y + C × y = P(t) , |
|
|
|
|
||||
|
|
&& |
& |
|
|
|
|
|
|
|
где учтено, что изменение силы неупругого сопротивления в соответствии с |
||||||||||
гипотезой Кельвина-Фойгта пропорционально скорости колебания |
системы |
|||||||||
( Fс = -b × y ), |
где b коэффициент пропорциональности. При P(t) = 0 (свободные |
|||||||||
& |
|
|
|
|
|
|
|
|
|
|
колебания), |
поделив все члены на М и обозначая: 2 ×ε = |
b |
; |
ω 2 = |
C |
, |
получим |
|||
|
|
|||||||||
|
|
|
|
|
M |
|
M |
|
||
дифференциальное уравнение свободных колебаний системы с одной степенью свободы с учетом сил неупругого сопротивления:
|
|
|
|
|
|
|
|
y + 2 ×ε × y + ω |
2 |
× y = 0 . |
|
|
|
|
|
(7.1) |
||||||||
|
|
|
|
|
|
|
&& |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В выражении (7.1) |
ε |
называют коэффициентом демпфирования (или |
|||||||||||||||||||||
затухания). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение уравнения (7.1) имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y = e−ε t (a1 × cos ω1t + b1 × sin ω1t) , |
|
(7.2) |
|
|
|||||||||||||
|
ω = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
ω 2 - ε 2 |
(7.3) |
- |
частота |
|
собственных колебаний |
с |
учетом |
сил |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сопротивления. |
|
Так как |
ε PP ω , то на практике принимают ω1 = ω и записывают |
|||||||||||||||||||||
(7.2) |
в виде: y = e−ε t (a1 × cos ω t + b1 × sin ω t) . |
Произвольные постоянные |
|
a1 и |
|
b1 |
||||||||||||||||||
определяются из начальных условий: |
|
|
|
|
|
|
|
|
|
|
|
0 + ε × y0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||
в момент времени t = 0 , y = y0 |
= a1 , y = y0 |
= -ε × a1 + b1 ×ω , откуда: |
b1 |
= |
|
& |
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
& & |
|
|
|
|
|
|
|
|
|
ω |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда общее решение (7.2) примет вид: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
& |
|
+ ε × y0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y = e −ε t ( y0 |
× cos ω t + |
y0 |
× sin ω t) . |
|
|
|
|
(7.4) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|||
Выражение (7.4) есть уравнение свободных колебаний (движения) системы с одной степенью свободы с учетом сил неупругого сопротивления.
Это же уравнение можно записать и в другой форме:

58
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = a × e−ε t sin (ω t +α ) , |
(7.5) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
где: |
|
a и |
α |
- |
произвольные постоянные, |
||||||||
|
|
|
|
|
|
|
|
|
|
определяемые |
также из |
начальных |
|||||||||||
|
|
|
|
|
|
|
|
|
|
условий. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
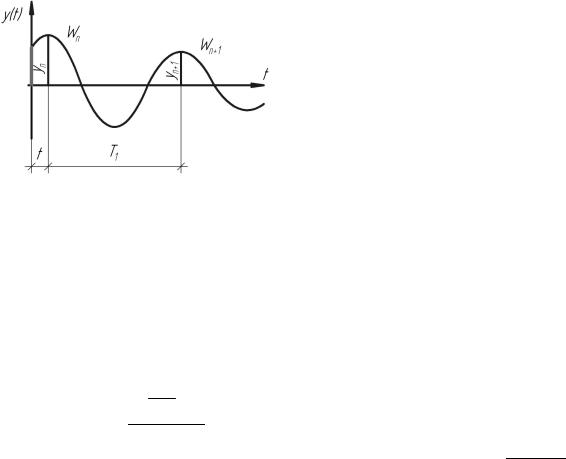
На |
|
|
рис. |
|
|
7.2 |
показан |
график, |
|||||
|
|
|
|
|
|
|
|
|
|
характеризующий |
движение |
системы с |
|||||||||||
|
|
|
|
|
|
|
|
|
|
учетом сопротивления среды. |
|
||||||||||||
|
|
|
|
|
|
Рис. 7.2 |
|
T = |
|
2 ×π |
|
- период колебаний с учетом сил |
|||||||||||
|
|
|
|
|
|
ω1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
сопротивления. |
|
|
|
|
|||||||||
Выразим логарифмический декремент затуханий: |
|
|
|
|
|||||||||||||||||||
δ = ln |
y |
n |
|
= ln |
a × e |
−ε t sin (ω t + α ) |
|
= ln |
1 |
|
= ln eε T1 =ε ×T . |
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
(7.6) |
||||||||||||||
|
|
|
a × e−ε (t +T1 ) sin[ω1 (t + T1 ) + α ] |
e−ε |
|
||||||||||||||||||
|
|
yn+1 |
|
|
|
|
T1 |
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
γ = |
ψ |
|
= |
2 ×δ |
|
= δ ; |
|
δ = γ ×π = ε ×T1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 ×π |
|
|
2 ×π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8.Вынужденные колебания системы с одной степенью
свободы при действии гармонической нагрузки
Рассмотрим систему по рис. 8.1 с одной степенью свободы, находящейся под действием гармонической нагрузки
P(t) = P × sinθ t , приложенной к сосредоточенной массе M.
Дифференциальное уравнение движения этой системы:
|
&& |
& |
|
M × y |
+ b × y + C × y = P ×sin θ t . |
Рис 8.1 |
Поделив левую и правую части уравнения |
|
на M и обозначив P = P , получим дифференциальное уравнение вынужденных
M
колебаний системы с одной степенью свободы от действия гармонической нагрузки:
|
|
|
|
|
|
|
|
|
|
|
|
y + 2 ×ε × y + ω |
2 |
× y = P × sin θ t . |
(8.1) |
||||||
|
&& |
|
& |
|
|
|
|
|
|
|
Решение этого дифференциального уравнения ищут как сумму общего |
||||||||||
решения, выражающего свободные колебания и имеющего вид: |
|
|||||||||
|
y |
c |
= e−ε t (a |
× cos ω t + b × sin ω t) , |
|
|||||
|
|
1 |
|
|
1 |
|
|
|||

59
ичастного решения неоднородного дифференциального уравнения,
выражающего вынужденные колебания, которое ищут в виде:
yb = A1 × sin (θ t - β ) ,
где: A1 - частота вынужденных колебаний, θ - частота нагрузки; β - угол сдвига
по фазе между гармонической нагрузкой и вынужденными колебаниями. Таким образом полное решение дифференциального уравнения имеет вид:
y = e−ε t (a1 × cos ω t + b1 × sin ω t) + |
A1 ×sin (θ t - β ) . |
(8.2) |
|||
Для получения выражения угла сдвига по фазе |
β и амплитуды |
||||
вынужденных колебаний A1 , проделаем следующее: обозначим |
Ω =θ t − β . Тогда: |
||||
yb = A1 ×θ × cos W , |
yb |
= -A1 ×θ |
2 |
× sin W . |
|
& |
&& |
|
|
|
|
Подставляя в (8.1), получим:
- A1 ×θ 2 sin W + 2 ×ε × A1 ×θ × cos W + ω 2 × A1 × sin W = P ×sin (W + β ) = P × (sin
Приравняем коэффициенты при sin Ω и cos Ω . Получим:
- A ×θ 2 |
+ A ×ω 2 |
= |
P |
× cos β ; |
|
1 |
1 |
|
|
|
|
2 ×ε × A1 ×θ = |
|
× sin β , |
|||
P |
|||||
откуда:
tg β = |
2 ×ε ×θ |
. |
|
|
|||
|
ω 2 -θ 2 |
|
|
W × cos β + cos W × sin β ).
(8.3)
(8.4)
Обозначим отношение частот через λ = θ , умножим и разделим правую часть |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(8.4) на ω 2 и учитывая, что ε = γ ×π , получим окончательно: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 ×ε ×θ / ω 2 |
|
2 ×ε ω × |
|
|
= |
|
2 |
×ε × λ |
× |
|
|
|
|
|
= |
γ ×π × λ |
× |
|
|
= |
|
γ × λ |
|
, tg β = |
γ × λ |
. |
|
|||||||||||||||||||
tg β = |
= |
ω |
2 ×π |
π |
(8.5) |
||||||||||||||||||||||||||||||||||||||||||
|
1 - λ2 |
|
|
1 - λ2 |
|
|
|
|
|
|
1 - λ2 |
|
|
|
1 - λ2 |
1 - λ2 |
|
1 - λ2 |
|
|
|
|
|||||||||||||||||||||||||
|
Возведем в квадрат правые и левые части выражений (8.3). Получим: |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 2 |
× (ω 2 -θ 2 )2 |
= |
|
|
2 × cos 2 β |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ×ε |
2 × A 2 |
×θ 2 |
= |
|
|
2 × sin 2 β . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Складывая, будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 = A |
2 |
× (ω 2 |
-θ 2 ) + 4 ×ε 2 × A 2 ×θ 2 |
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
откуда выражение для |
|
амплитуды вынужденных колебаний примет вид: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω 2 |
|
|
|
|
|
|
|
|
Pω 2 |
|
|
|
|
|
|
|
|
|
|
|
|
D * |
|
|
|
|
|||||||
A1 = |
|
|
|
|
P |
|
|
|
|
|
× |
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
, |
(8.6) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ω 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(ω 2 -θ 2 )2 + 4 ×ε 2 ×θ 2 |
|
|
(1 - λ2 )2 + γ 2 × λ2 |
(1 - λ2 ) 2 + γ 2 × λ2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
где:
