
10055
.pdf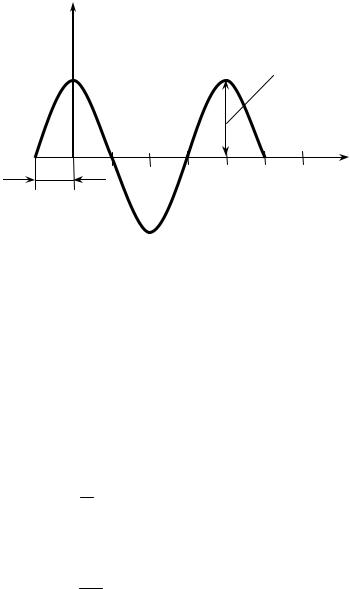
20
Угол α равен произведению угловой скорости вращения рамки ω на время
t.
α = ω × t
Таким образом, ЭДС, возникающая в рамке, будет равна
e = Em sinα = Em sinω t (В) |
(3.1) |
3.2. Способы изображения синусоидальных величин
Под переменной ЭДС понимается ЭДС, изменяющаяся по синусоидально- му закону (рис. 3.2).
e(B)
Em
φE |
0 |
ωt |
|
||
|
|
Рис. 3.2
Закон изменения синусоидальной ЭДС записывается в следующем виде:
e = Em sin(ω t +ϕE ) (В), |
(3.2) |
где e – мгновенное значение ЭДС (В), это значение ЭДС в каждой точке синусоиды;
ω t +ϕE – фаза синусоидальных колебаний; ϕE – это начальная фаза для t = 0;
ω – угловая частота синусоидальных колебаний (1/с). Частотой f называется число периодов в секунду:
f = 1 (Гц),
T
где T – период, это время одного цикла колебаний (с). Угловая частота ω и частота f связаны соотношением:
ω = 2π = 2π × f .
T
Для источника переменного напряжения закон изменения записывается в следующем виде:

21 |
|
|
u =U m sin(ω t +ϕU ) |
(В) |
(3.3) |
Для синусоидального тока закон изменения записывается аналогичным |
||
образом: |
|
|
i = I m sin(ω t + ϕI ) |
(А) |
(3.4) |
При сравнении выражений (3.2), (3.3), (3.4) видно, что форма записи оди- накова, разница лишь в угле начальной фазы ϕ .
Частота переменного тока f = 50 Гц в Европе и 60 Гц в США и Японии. Для того, чтобы сравнить характеристики цепей постоянного и переменно-
го токов, вводится понятие действующего значения синусоидальной величины:
|
1 |
T |
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
||||||
тока I = |
Im2 sin 2 ω t × dt = |
|
|
|
|
|
|
|
|
|||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
|
|
U |
|
|
|
|
напряжения U = |
U m2 sin 2 ω t × dt = |
m |
|
; |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
T |
0 |
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
T |
|
|
|
E |
|
|
|
|
|
|
|
|
|
||||||
ЭДС E = |
|
Em2 sin 2 ω t × dt = |
m |
|
. |
|||||||||||||||||
|
T |
|
|
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
Электроприборы в цепях переменного тока измеряют действующее значе- ние тока, напряжения, ЭДС и мощности.
Тригонометрическая форма записи синусоидальных величин неудобна при расчёте электрических цепей переменного тока, поэтому в электротехнике си- нусоидальные функции изображают в виде комплексных чисел, согласно сле- дующему положению.
Любая синусоидальная функция может быть изображена в виде вектора на комплексной плоскости, величина которого равняется синусоидальной функ- ции, а угол, образованный с осью действительных чисел, равняется углу начальной фазы синусоидального колебания.
Комплексная плоскость – это плоскость, образованная с осью действи- тельных чисел (+ 1) и осью мнимых чисел (+ j), где j 2 = −1.
∙
На рис. 3.3 показано изображение амплитуды тока I m на комплексной плоскости
+ j
∙
Im
Imм
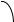 φ
φ
Imд |
+ 1 |
|
Рис. 3.3

22
∙
Из рис. 3.3 следует, что I m – комплекс I m (точка показывает комплексную величину); Imд – проекция комплекса на ось действительных чисел; I mм – про- екция комплекса на ось мнимых чисел; ϕ – угол начальной фазы.
Существуют следующие способы изображения комплексных чисел: алгебраическое
|
|
|
|
|
|
|
|
∙ |
|
|
||
|
|
|
|
|
|
|
|
I m = Imд |
+ jI mм ; |
|||
|
|
тригонометрическое |
|
|
||||||||
|
|
|
|
|
|
|
|
∙ |
(cosϕ + j sinϕ); |
|||
|
|
|
|
|
|
|
|
I m = |
Im |
|||
|
|
|
|
|
|
|
|
, ϕ = arctg |
I mм |
. |
||
где |
|
Im |
|
= Im2 |
д + I m2 |
м |
||||||
|
|
|||||||||||
|
|
|
|
|||||||||
|
|
показательное |
|
|
I mд |
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
∙ |
× e+ jϕ ; |
|||
|
|
|
|
|
|
|
|
I m = |
I m |
|||
где e – основание натуральных логарифмов.
∙ ∙
Аналогично изображаются и комплексы напряжений U и ЭДС E .
Рассмотрим пример, когда требуется определить сумму двух токов
,изображённых на комплексной плоскости (рис. 3.4).
+j
∙
∙ |
I3 |
I1
∙
I 2
(3.5)
(3.6)
(3.7)
∙∙
I 1 и I 2
+ 1
Рис. 3.4
Взаимное расположение векторов на комплексной плоскости называется
∙ ∙ ∙
векторной диаграммой. Для определения суммы двух токов I 3 = I1 + I 2 доста-
точно сложить их по правилу параллелограмма.
Применение комплексных чисел при расчёте электрических цепей пере- менного тока позволяет перейти от дифференциальных и интегральных уравне- ний к алгебраическим.
23
3.3. Резистор в цепи однофазного переменного тока
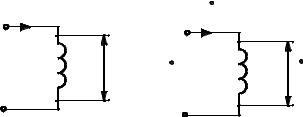
Пусть в цепь переменного тока i = I m sin ω t включен резистор R (рис. 3.5).
a) |
i |
б) I |
|
u ~ |
R |
uR |
UR |
|
|
U ~ R |
Рис. 3.5
Падение напряжения на резисторе определим согласно закону Ома:
uR = R × i = R × Im sinω t |
(3.8) |
где U m = R × I m .
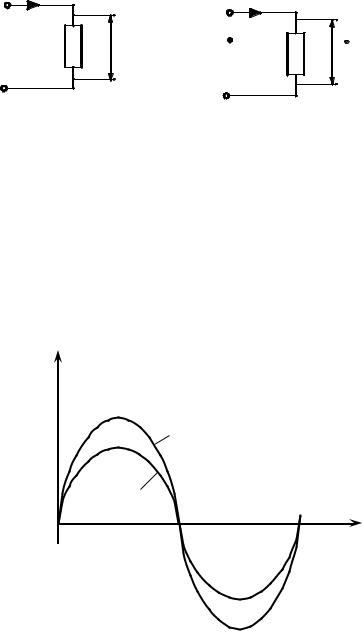
Графики изменения тока i и падения напряжения uR показаны на рис. 3.6. Построим векторную диаграмму для цепи, содержащей резистивный эле-
мент. Построение начнём с комплексной плоскости (рис. 3.7). Параллельно оси
∙
действительных чисел (+ 1) строим вектор действующего значения тока I .
uR, i
|
uR |
i |
|
0 |
2π ωt |
π |
Рис. 3.6
Далее, сравнивая законы изменения тока i и падения напряжения u R (рис.
3.6), делаем вывод: так как законы изменения тока i и падения напряжения на
∙
резисторе u R одинаковы, то вектор U R совпадает по направлению с вектором
∙
тока через резистор I (рис. 3.7).

24
+ j
∙
 U R
U R
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 |
|
|
|
|
|
Рис. 3.7 |
|
|
|||||
Поэтому закон Ома в комплексном виде запишется так: |
|
||||||||||
|
|
|
∙ |
|
|
∙ |
|
|
|||
|
|
|
U R = R × I |
|
(3.9) |
||||||
Этой форме записи закона Ома соответствует схема замещения, показан- |
|||||||||||
ная на рис. 3.5б. |
|
|
|
|
|
|
|
|
|
|
|
Мгновенная мощность на резисторе равна: |
|
|
|||||||||
p = u ×i = I U |
|
sin2 |
ω t = |
ImUm |
[1- cos 2ω t] |
|
(3.10) |
||||
m |
|
|
|
||||||||
|
m |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Из выражения (3.10) видно, что мгновенная мощность содержит постоян- |
|||||||||||
ную составляющую |
ImUm |
и переменную |
ImUm |
cos 2ω t . |
|
||||||
|
|
|
|||||||||
2 |
|
|
2 |
|
|
|
|||||
Среднее значение мощности, выделяемой на резистивном элементе, равно: |
|||||||||||
|
|
|
P = |
Um Im |
=U × I = I 2 × R |
(Вт), |
(3.11) |
||||
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
где I = U R
Мощность Р называется активной и измеряется в ваттах (Вт).
25
3.4. Индуктивность в цепи переменного тока (индуктивный элемент)
Пусть в цепь переменного тока i = I m sin ω t включена индуктивность (рис. 3.8, а).
a) |
i |
|
б) |
I |
|
|
|
|
|
||
|
|
|
|
|
|
u ~ L |
uL |
U ~ |
X L |
U L |
|
|
|
|
|||
Рис. 3.8
Известно [1], что при прохождении тока через индуктивный элемент в нём возникает магнитный поток Φ , который наводит в нем ЭДС самоиндукции
|
|
eL = -W |
dΦ |
= -L |
di |
, |
(3.12) |
dt |
|
||||||
|
|
|
|
dt |
|
||
где W – число витков катушки индуктивности. |
|
||||||
Эта ЭДС самоиндукции уравновешивается падением напряжения на ин- |
|||||||
дуктивности u L |
|
|
|
|
|||
|
|
eL = − uL |
|
|
|
(3.13) |
|
Падение напряжения на индуктивности u L с учётом (3.12) и (3.13) будет |
|||||||
равно |
|
|
|
|
|||
uL = L |
di |
= ωL × Im cosω t = ωLIm sin (ω t + 900 ) |
(3.14) |
||||
|
|||||||
|
dt |
|
|
|
|
||
|
|
uL =U m sin(ω t + 900 ) |
|
||||
Введём понятие индуктивного сопротивления X L |
|
||||||
|
|
X L =ωL = 2π fL = 314L , (Ом) |
(3.15) |
||||
где f = 50 Гц. |
|
|
|
|
|||
Графики изменения тока ( i ) и падения напряжения на катушке ( u L ) пока- заны на рис 3.9.
26
uL, L
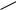 uL
uL
i
0 |
π |
3/2 π 2π |
ωt |
π/2 |
Рис. 3.9
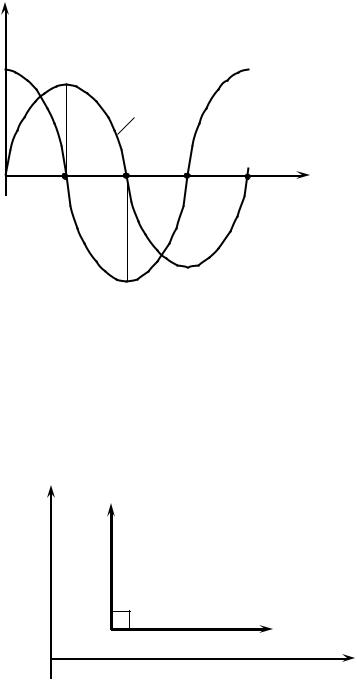
Из рис. 3.9 следует, что ток i и падение напряжения u L колеблются в про-
тивофазе.
Построим векторную диаграмму для цепи, содержащей индуктивность L. Построение начинаем с комплексной плоскости (рис. 3.10). Параллельно оси
|
∙ |
|
строим вектор действующего значения тока |
∙ |
действительных чисел |
+1 |
I . |
||
|
|
|
|
|
|
|
|
|
|
+ j |
|
|
∙ |
|
|
|
|
U L |
|
90º
∙
I
+ 1
Рис. 3.10
Теперь, сравнивая (рис. 3.9) законы изменения тока sin ω t и падения напряжения на индуктивности U m × sin(ω t + 900 ), делаем вывод, что вектор па-
|
∙ |
∙ |
π . |
дения напряжения на индуктивности U L |
опережает вектор тока I на угол |
||
|
|
|
2 |
Закон Ома в комплексном виде для индуктивного элемента запишется |
|||
∙ |
∙ |
|
|
U L = + jX |
I , |
|
(3.16) |
|
L |
|
|
где + jX L – комплекс индуктивного сопротивления;
27
|
|
∙ |
|
∙ |
на угол π . |
+ j показывает, что вектор U L опережает вектор I |
|||||
Мгновенная мощность индуктивности равна: |
2 |
||||
|
|||||
qL = uL × i = Im sin ω t ×U Lm cosω t = U L I sin 2ω t |
(3.17) |
||||
Мощность в цепи, содержащей индуктивный элемент, называют реактив- |
|||||
ной индуктивной мощностью (+ QL) и измеряют в вольт-амперах реактивных |
|||||
(вар). |
|
|
|
|
|
+ Q |
L |
= I 2 X |
L |
(вар) |
(3.18) |
|
|
|
|
||
3.5. Конденсатор в цепи переменного тока
Пусть в цепь переменного напряжения u = U m sinω t включен конденсатор
(рис. 3.11). |
|
|
|
|
|
|
Тогда ток, проходящий через конденсатор будет равен [1]: |
|
|||||
iA = C duC =ωCUm cosω t = Im cosω t = Im sin (ω t +900 ), |
(3.19) |
|||||
dt |
|
|
|
|
|
|
где Im =ωCU m . |
|
|
|
|
|
|
Введём понятие ёмкостного сопротивления XC |
|
|
||||
X |
|
= 1 = |
1 |
= 1 |
, (Ом) |
(3.20) |
|
C |
ωC |
2π fC |
314C |
|
|
где f = 50 Гц, емкость С измеряется в фарадах (Ф). |
|
|||||
a) |
|
|
б) |
|
|
|
ic |
|
|
|
I C |
|
|
|
|
|
|
|
|
|
u~ |
|
uc |
U~ |
X C |
U C |
|
|
|
|
|
|||
C |
|
|
|
|
||
Рис. 3.11
Графики изменения напряжения на конденсаторе uC и тока i показаны на рис. 3.12.

28
uC, i
|
uC |
|
|
|
i |
|
|
0 |
π |
3/2 π 2π |
ωt |
π/2 |
Рис. 3.12
Построим векторную диаграмму для цепи, содержащей конденсатор. По- строение начинаем с комплексной плоскости (рис. 3.13). Параллельно оси дей- ствительных чисел (+ 1) строим вектор действующего напряжения на конденса-
∙
торе U C . Теперь, сравнивая (рис. 3.12) законы изменения напряжения на кон-
денсаторе uC = U m × sinω t |
и тока i |
через конденсатор Im ×sin (ωt + 90)0 |
делаем |
|
|
∙ |
|
вывод, что вектор тока I опережает вектор падения напряжения U C на конден- |
|||
π |
|
|
|
саторе на угол 2 . |
|
|
|
Закон Ома в комплексном виде для конденсатора запишется так: |
|
||
|
∙ |
∙ |
|
|
U C = - jX C IC , |
(3.21) |
|
где − jX C – комплекс емкостного сопротивления; |
|
||
|
|
∙ |
|
− j показывает, что падение напряжения на конденсаторе U C отстает |
|||
∙ |
|
|
|
от тока I C на угол π . |
|
|
|
2 |
|
|
|
+ j |
∙ |
|
|
|
I C |
|
|
90º
∙
U C
Рис. 3.13 |
+ |
Этой форме записи закона Ома в комплексном виде соответствует схема замещения, показанная на рис. 3.11, б.

29
Мгновенная мощность на конденсаторе равна
qC = uC × iC = U m sin ω t × Im cosω t = U m Im sin 2ω t |
(3.22) |
||
Мощность в цепи, содержащей емкостный элемент, называют реактивной |
|||
емкостной мощностью QC и измеряют в вольт-амперах реактивных (вар). |
|
||
− Q = I 2 X |
C |
(вар) |
(3.23) |
C |
|
|
|
Знак «минус» у мощности QC говорит о том, что в первую и третью чет- верть колебаний конденсатор отдаёт мощность источнику в отличие от индук- тивности, которая в первую и третью четверть потребляет от источника реак- тивную мощность +QL.
3.6.Последовательное соединение резистора, индуктивности
иёмкости в цепи переменного тока
Последовательным соединением элементов называется такое соединение, когда по всем элементам идёт один и тот же ток, а приложенное напряжение равняется геометрической сумме падений напряжений на этих элементах со- гласно второму закону Кирхгофа.
Схема последовательного соединения R, xL, и xC приведена на рис. 3.14, а.
а) |
|
R |
X L |
X C |
|
|
|
I |
б) |
I |
|||
|
|
|
|
|||
U~ |
|
U R |
U L |
U C |
U ~ |
Z |
|
|
|
Рис. 3.14
Второй закон Кирхгофа в комплексном виде запишется следующим обра-
зом:
|
|
|
|
|
|
|
|
∙ |
|
∙ |
∙ |
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
U |
|
=U R |
+U L +U C |
|
|
|
(3.24) |
|||||
С учетом вышеприведённых выражений |
|
|
|
|
||||||||||||||
|
|
∙ |
∙ |
|
|
∙ |
|
|
|
∙ |
|
|
|
∙ |
[R + j(xL − xC )] |
|
||
|
|
U = I R + I |
(+ jxL )+ I (− jxL )= I |
(3.25) |
||||||||||||||
Выражение в квадратных скобках обозначим через Z и назовем его полным |
||||||||||||||||||
комплексным сопротивлением цепи. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Z = R + j(xL − xC ) |
|
|
(Ом) |
(3.26) |
||||||||
По величине |
|
Z |
|
|
равняется |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||
|
|
|
|
|
Z = |
|
Z |
|
R2 + (x |
L |
− x |
)2 |
|
(Ом) |
|
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
Тогда закон Ома для последовательно соединенных элементов в комплекс- ной форме запишется в виде
