
9939
.pdf
§4. Извлечение корней из комплексных чисел
7.15. Представить в показательной форме числа: 1) z 2i ; 2) |
z 1 i ; 3) 1; 4) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 i ; 5) 3 i 3 ; 6) 2 i 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.16. Представив числа z1 1 i |
и z2 1 i 3 в показательной форме, вычислить: |
||||||||||||||||||||||
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) z1 z2 ; 2) |
; 3) z16 ; 4) 4 z1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
7.16. Извлечь корни из комплексных чисел: 1) i ; 2) 3 1 ; 3) 4 |
1 ; 4) 3 i ; 5) 4 4 ; |
||||||||||||||||||||||
6) 4 2 2i
 3 ; 7) 6
3 ; 7) 6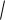 1 .
1 .
7.17. Найти корни многочлена второй степени (с комплексными коэффициентами) на множестве комплексных чисел и разложить его на
2
множители Q(x)ix2ix13i .
7.18. Составить квадратное уравнение с действительными коэффициентами,
если известен один из его корней x 1 3i.
1
2
7.19. Решить на множестве комплексных чисел уравнение 4x 8x 130.
Глава 8
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
§1. Непосредственное интегрирование
В задачах 8.1 - 8.24 вычислить интегралы:
8.1. x 23dx. x
x 4 8.4. 2 x dx.
|
x 13 |
8.7. |
dx. |
|
x |
1 x2
8.10. 2 dx. x 1 x
8.13.21 dx.
x7
|
x 1 |
|
|
|
|
|
|||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
8.2. |
|
3 |
|
dx. |
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
8.5. |
|
|
|
|
|
|
|
dx |
|||
|
|
|
|
|
|
4 3 |
|
||||
|
x |
|
|
x |
|
|
|
||||
1 x 2
8.8. dx.
x
8.11. 21 dx. x 27
dx
8.14.  5 x2 .
5 x2 .
8.3.3x 21dx.
 x
x
3 2 4
x 
 xdx.
xdx.
 x
x
2
12x
8.9.2 2 dx.
x1 x
8.12.2x2 dx.
x1
dx
8.15. 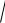 4 x2 .
4 x2 .
70

dx
8.16. 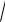 x2 9.
x2 9.
2
8.19. ctgxdx.
8.22. 3xexdx.
8.25.Будет ли
sin2x 1?
|
|
|
|
|
cos2x |
dx |
||
8.17. |
|
|
|
|
|
|||
|
2 2 . |
|||||||
|
|
|
cosxsinx |
|||||
|
|
|
|
|
2 |
|
|
|
|
|
3tgx 3 |
||||||
8.20. |
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||
|
2 . |
|
||||||
|
|
|
|
sinx |
||||
|
|
|
|
x |
x |
|||
8.23. |
|
2 |
5 |
dx |
||||
|
|
|
||||||
|
x . |
|||||||
|
|
|
|
10 |
|
|
|
|
8.18. tg2xdx.
|
|
x |
|
x |
|
e |
|
|
|
||
e 1 |
2 |
dx |
|
8.21. |
|
. |
|
|
cosx |
||
|
|
|
|
3 x 2
8.24. xe 3 x dx. x
1
функция cos2x 1 2первообразной для функции
2
8.26. |
Пусть F x |
- первообразная для функции |
|
1 |
|
|
и F 1 . |
|
|
|
|
|
|||||
|
|
|
|
|||||
2 |
||||||||
|
|
|
|
2 |
||||
|
|
|
|
5 4x x |
||||
Найти |
F 2 . |
|
|
|
|
|
|
|
§2. Интегрирование внесением под знак дифференциала или методом замены переменной
В задачах 8.27 - 8.64 вычислить интегралы:
|
|
2xdx |
|
7 |
|
|
|
|
|||
|
|
|
2 3xdx |
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
8.27. |
|
|
. |
|
|
. |
8.30. |
||||
|
x2 |
8.28. 2 3x dx.8.29. |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
53 5xdx |
|
|
|
|
|
|
|
|
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
. |
|
8.31. |
|
|
|
8.32. |
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 3x |
|
|
|
. |
|
|
|
3 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||
|
|
|
|
1 3x |
|
|
|
2x 3 |
|
|
|
|
|
|
x 1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||||
8.34. |
|
3 2x |
.8.35. |
|
2x 1 . |
8.36. |
x2 1 . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
6x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
dx |
|
|
|
|
|
x lnx |
|
|
|
|
|
||||||||||||||
8.38. |
|
|
|
|
8.39. |
|
|
|
|
|
|
|
|
dx |
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
x |
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
23x 5x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x3 dx
8.33.  .
.
 x4 1
x4 1
8.37.3x2 dx
x1
lnx
8.40. x dx.8.41.
xdxln x .
8.45. ex dx.
x
e 1
1 sinx
2 dx. cosx
cosx dx
3 2 .
 sinx
sinx
8.42. |
e3x dx. |
|
|
|
|
8.43. e xdx.8.44. |
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
dx |
|
|
sinx |
dx |
|||
8.46. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
2x |
.8.47. |
2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
cosx |
|
|||||
|
|
|
|
|
|
9 e |
|
|
|
|
||||||
|
|
sinx |
|
|
|
|
sin2x |
dx |
||||||||
|
e |
|
|
cosxdx |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
8.49. |
|
|
|
|
|
|
|
|
.8.50. |
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
cosx |
|
||||
5 2
8.52.cosxsin2xdx. 8.53. xsin1xdx.
e
 x dx.
x dx.

 x
x
8.48.
8.51.
8.54.
|
tgx |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
ctgx |
|
|
|
|
||||
|
dx |
|
|
|
arctgx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
. |
8.55. 2 dx. 8.56. |
|
2 dx. |
8.57. |
||||||
|
cosx |
|
|
sinx |
|
|
1 x |
|
|||||
|
|
|
|
71 |
|
|
|
|
|
||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3arcsinx |
||||||||||
|
2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
dx |
|||
|
|
|
1 x |
|||||||||
|
|
3x arcsinx |
||||||||||
|
2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
||
|
|
|
|
1 x |
||||||||
|
|
|
|
dx |
||||||||
|
|
. |
||||||||||
|
|
|
||||||||||
2 |
||||||||||||
|
|
|
1 2x x |
|||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||
8.58. |
|
|
|
|
|
|
|
|
|
. |
8.59. |
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
2 |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
4 2x 3 |
|
|
|
arccosx 1x |
|
|||||||||||
8.61. |
|
|
|
dx |
|
.8.62. |
|
dx |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x 2x 2 |
|
|
4x 3 x |
|
|
|
|||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.64. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
§3. Интегрирование по частям
8.60.
8.63.
В задачах 8.65 - 8.92 вычислить интегралы:
8.65. x sinxdx.
8.68. exx dx.
x
8.71. 2 dx. sinx
8.74. x sinxdx.
8.77. lnxx dx.
8.80. arcsinxdx.
8.83. xarcctgxdx.
2
8.86. x sinxdx.
2 x
8.89. x 2 dx.
8.92. Вычислить разность функции x ln x .
8.93. Вычислить разность функции x 6cos3x.
8.66. x cos2xdx.
2x
8.69. 3 x e dx.
8.72. x2 dx. cosx
8.75.ln xdx.
8.78.lnx3xdx.
arcsinx 8.81. dx.
 1 x
1 x
|
|
|
|
|
|
|
|
arctgx |
|
||||
|
|
|
|
|
dx |
|
8.84. |
|
|
|
|||
x |
|
|
. |
|||
|
|
|
|
|
||
8.87. ln2 xdx.
x
8.90.e sinxdx.
F2 F1, если F x
8.67.5x 6sin3xdx.
x
8.70.x 2 dx.
x cosx 8.73. 2 dx.
sinx
8.76.xlnx 1dx.
2
8.79.lnx 1dx.
8.82.arctgxdx.
|
|
|
|
|
|
|
|
|
arcsinx |
|
|||
8.85. |
|
|
|
|
dx |
|
|
|
|
|
|||
|
1 x |
|
. |
|||
|
|
|
||||
2 x
8.88.x e dx.
x
8.91.e cosxdx.
-первообразная для
|
|
|
|
F x |
|
F2 F |
- первообразная для |
|
, если |
|
|
|
|
|
3 |
|
|
72

§4. Интегрирование рациональных функций
В задачах 8.94 - 8.113 вычислить интегралы:
x
8.94. x 2dx.
dx
8.97. x 2x 3.
2x 7dx
8.100. 2 . x x 2
x3 1
8.103. 3 dx. x x
8.106. |
x3 1 |
dx |
||
|
||||
|
3 |
. |
||
|
x |
|
x |
|
dx
8.109. x x2 1 .
8.95.x2 dx.
x3
dx
8.98. x 12x 3.
xdx
8.101. 2 .
2x 3x 2
|
|
|
dx |
|
|||||
8.104. |
|
|
|
. |
|
||||
x x 12 |
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x x 1 |
|
||||
8.107. |
|
|
|
|
|
|
dx |
||
|
4 |
|
|
||||||
|
|
|
|
. |
|||||
|
|
|
|
x x |
|
||||
8.110. |
|
|
|
dx |
|
. |
|
|
|
|
|
3 |
|
|
|
||||
|
|
x 1 |
|
|
|
|
|||
8.112. |
|
x 2 |
dx |
8.113. |
|
x 2 |
dx |
||
|
|
|
|
||||||
4 |
. |
3 2 |
. |
||||||
|
|
x 1 |
|
|
|
x 2x x |
|
||
8.96.
8.99.
8.102.
8.105.
8.108.
8.111.
x4
2 dx. x 2
x 4dx
.
x 2 x 3
3x 2x 3
2
3 dx. x x
|
|
x 2 |
dx |
||
|
|
|
|||
3 |
x |
. |
|||
|
|
x |
|
||
|
|
x 1 |
dx |
||
|
|
|
|||
4 |
2 . |
||||
|
x |
x |
|
||
xx3dx1 .
§5. Интегрирование тригонометрических функций
В задачах 8.114 - 8.131вычислить интегралы:
sin3xsin7xdx |
sin2xcos6xdx |
|
x |
x |
||
coscodxs |
||||||
8.114. |
. 8.115. |
|
. |
8.116. |
3 |
2 . |
3
8.117. sinxdx.
3
cosx
8.120. 2 dx. sin x
8.123. tg4xdx.
4
8.126. cosxdx.
8.118.
8.121.
8.124.
8.127.
5
cosxdx .
3
sincosxxdx.
|
2 x |
. |
||
sin |
|
dx |
||
|
|
2 |
|
|
3sindxx .
2 3
8.119. sinxcosxdx.
3
8.122. ctg xdx.
2 x
8.125. cos2dx.
dx
8.128. 5cos2x.
73

|
|
dx |
|
|
dx |
|
|
|
dx |
||
8.129. |
|
|
. 8.130. |
|
|
|
. |
8.131. |
|
|
. |
|
|
1 sinx |
|
||||||||
|
5cosx 3 |
|
|
1 sinx cosx |
|||||||
§6. Интегрирование некоторых иррациональных функций
В задачах 8.132 - 8.148 вычислить интегралы
8.132. x 
 x 5dx.
x 5dx.
x
8.135. 1 xdx.
|
|
x 1 |
|
dx |
8.138. |
|
|
||
2x 1 . |
||||
1 dx
8.141. 4x 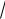 x .
x .
3 2
8.144. x 1 xdx.
|
|
|
1 |
|
|
dx |
|
|
|
|
|
|
|
||
8.147. |
|
|
|
|
|||
2 |
|
|
. |
||||
|
|
x x |
1 |
|
|||
|
1 |
|
|
|
dx |
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
8.133. |
1 x . |
|
8.134. |
|||||||
|
1 |
|
|
dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.136. |
1 x 1 . |
8.137. |
||||||||
1
8.139. dx. 8.140. x  x 1
x 1
|
|
|
1 |
|
|
dx |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
8.142. |
|
|
|
|
|
|
|
|
8.143. |
||||||
3 2 . |
|
||||||||||||||
|
|
x x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
8.145. |
x1 x dx. |
8.146. |
|||||||||||||
|
|
|
1 |
|
|
|
|
|
dx |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8.148. |
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
. |
|
|||||||
|
|
x x |
1 |
|
|
||||||||||
1
dx 
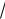 x 1 .
x 1 .

 x 2dx. x
x 2dx. x
x2 dx. 
 x 1
x 1
1
dx
1 3x 2 .
2
9 x dx.
§7. Смешанные примеры
8.149. |
Найти ту первообразную от функции |
|
1 |
x , которая принимает значение |
|||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 при |
x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
График первообразной F x |
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8.150. |
для функции |
|
|
|
|
|
|
|
|
|
|
|
проходит |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x 4 x 4 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
через точку |
A 5; 0 . Найти F 8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В задачах 8.151 - 8.198 вычислить интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4x |
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
4 |
|
|
5 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8.151. |
x1 x 2xdx. 8.152. |
|
x 1 6xdx. |
8.153. |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7x 1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2x 3dx |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
||||||||||||||
8.154. |
|
2 |
|
|
|
|
. |
8.155. |
|
|
|
|
|
. |
|
|
|
8.156. |
|
|
|
|
. |
|
|
||||||||||||
|
4 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|
|
|
1 9x |
|
|
|
|
|
|
|
2x |
9 |
|
|
|||||||||||||||||||
|
|
|
xdx |
|
|
|
|
|
|
|
ex dx |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||
8.157. |
|
4 |
|
|
|
. |
|
|
8.158. |
|
|
|
|
|
|
|
. |
|
|
|
|
8.159. e 1 e dx. |
|||||||||||||||
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x |
1 |
|
|
|
|
|
e |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

8.160.
8.163.
8.166.
8.169.
8.172.
8.175.
dx
x 2x.
e 1 e
1 xdx
 .
.
x
x 1
dx.
 1 x
1 x
2
xsinxdx.
2
x3 12dx. x x
sinxcos3xdx.
|
|
|
dx |
||||
8.161. |
|
|
|
|
. |
||
|
|
|
|
||||
2 |
|||||||
|
|
|
x 3 lnx |
||||
8.164. |
|
dx |
|||||
|
|
|
|||||
|
x 1 x . |
||||||
arccosx
8.167. 2 dx.
1 x
2
8.170. x tg xdx.
4
8.173. x 1dx.
3 2
x x
lnxdx
8.162. 2 . x 1 lnx
3 5 4
8.165. x 1 5xdx.
|
|
|
|
1 |
|
||
|
|
|
|
2 |
|||
|
|
|
sin |
|
dx |
||
8.168. |
|
|
x . |
||||
|
|
3 |
|
|
|||
|
|
|
|
x |
|
|
|
8.171. |
|
arctgxdx |
|||||
|
|
|
. |
|
|||
|
|
2 |
|
||||
|
|
|
x |
|
|
|
|
sin2x 8.174. dx.
5 cos2x
|
4 |
5 |
|
cos5xcosxdx |
|
sinxcosxdx |
|||||
8.176. |
|
|
. 8.177. |
. |
|
8.178.
8.181.
8.184.
8.1887
lnx3x dx.
x
2 dx
x
1 2
.
2
x
dx
8x 27
3
.
dx

 x 1 x .
x 1 x .
8.179.
8.182.
8.185.
8.188.
tgx dx
 cosx
cosx
.
3
1 tg xdx.
|
x |
|
dx |
|
|
|
|
||
|
2 x |
|||
|
||||
2 |
3 . |
|||
x2 2dx. cosx
|
x |
x |
|
2 |
|
2 |
2 |
|
|
sincosdx |
tg 4xdx. |
|||
8.190. |
2 |
2 |
. 8.191. |
|
|
|
|
||
8.193.
8.196.
dx
x x .
e 3 e
|
|
dx |
||
|
|
. |
||
|
|
|
||
2 |
||||
|
1 2x x |
|||
8.194. |
|
dx |
|||
2. |
|||||
|
|
2 6x 9x |
|||
|
|
|
x 2 |
|
dx |
8.197. |
|
|
|
||
2 . |
|||||
|
|
|
2x x |
||
8.180. 
 lnx2xdx.
lnx2xdx.
8.183. 2x dx.
1 4x
|
2 |
|
|
lnx 2 |
|
8.186. |
|
dx. |
|
||
|
x |
|
dx
8.189. co sx x.
sx x.
8.192. |
|
|
|
sin5x |
dx |
|||
|
|
|
|
|||||
|
|
5 cos5x |
. |
|||||
|
|
|
|
|||||
|
|
|
|
x 1 |
|
dx |
|
|
8.1965 |
|
|
|
|
||||
|
2x 1 . |
|
||||||
8.198. |
tg7xdx |
|
||||||
|
|
. |
|
|
|
|||
75
Глава 9
Определенный интеграл
§1. Непосредственное вычисление определённого интеграла и внесение функции под знак дифференциала
В задачах 9.1 - 9.12 вычислить интегралы:
|
3 |
|
|
|
|
|
|
|
|
|
4 |
dx |
|
|
|
|
|
9.1. 5x2dx. |
|
9.2. |
|
|
|
. |
|
||||||||||
|
cos |
2 x |
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
dt |
|
|
|
5 |
dx |
|
|
|
|
|||
9.5. |
|
|
|
|
. |
9.6. |
|
|
|
. |
|
||||||
|
|
|
|
|
|
3x 2 |
|
||||||||||
|
3t 4 |
|
|||||||||||||||
|
1 |
|
|
|
1 |
|
|
||||||||||
|
2 |
|
|
|
dx |
|
2 x 3 |
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9.9. |
|
2 |
|
|
|
|
. 9.10. |
|
2 |
|
|||||||
|
|
|
|
4 |
. |
||||||||||||
|
1x |
5x 4 |
0 x |
|
|||||||||||||
|
|
|
x |
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
||||
9.3. 1 e4 |
dx . |
9.4. |
|
|
|
dx. |
||||||||||||||
|
xe |
|||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
dx |
|
|
|
|
|
2 |
|
dx |
|
|
|
|
|
||||
9.7. |
|
|
|
|
|
. |
9.8. |
|
|
|
|
|
. |
|
|
|||||
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|||||||||
|
0 2x 1 |
|
|
1 x |
|
x |
|
|
|
|||||||||||
|
e ln2 xdx |
|
3 |
|
|
dx |
|
|
|
|||||||||||
|
e |
|
|
|
|
|
|
|||||||||||||
9.11. |
|
|
|
|
|
|
. |
9.12. |
|
|
|
|
|
|
|
|
|
. |
||
|
x |
|
|
|
|
|
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
1 lnx |
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
§2. Замена переменной в определённом интеграле
В задачах 9.13 - 9.24 вычислить интегралы:
4 1
9.13. dx.
01  x
x
13 x 1
9.16. 3 dx.
0 2x 1
2x 1
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
dx |
||||||||
9.19. |
|
|
||||||||
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|||||
2 |
2 |
|||||||||
|
2 x x 4 |
|||||||||
|
|
|
|
|||||||
e41 lnx |
||||||||||
|
|
|
|
|
|
|
|
dx |
||
9.22. |
|
|
|
|||||||
x |
. |
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
4 |
1 |
|
|
|
|
||||||
|
|
|
|
|
|
dx |
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
9.14. 1 2x 1 . |
|||||||||||
0 |
|
|
|
|
|
|
|
|
|||
0 |
|
dx |
|
||||||||
9.17. |
|
|
|||||||||
1 3 |
x 1. |
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|||
ln2 |
|
|
|
|
|
|
|
|
|||
x |
1dx |
||||||||||
|
|
|
|||||||||
9.20. |
e |
||||||||||
|
|
|
. |
|
|||||||
0 |
|
|
|
|
|
|
|
|
|||
9.23. 4 2tgx 7dx.
2 2
0cosx 9sinx
1xdx
9.15.1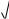 5 4x .
5 4x .
1
2
9.18.4 x dx.
0
ln8 dx
9.21. 1 ex .
ln3
3 x
9.24.0 6 xdx.
§3. Интегрирование по частям в определённом интеграле
В задачах 9.25 - 9.36 вычислить интегралы:
1 |
|
|
|
|
|
|
|
9.25. xe x dx. |
9.26. |
2 |
. |
0 |
|
x 1cosxdx |
|
|
0 |
|
|
|
|
|
|
9.27. xsinxdx.
0
76






 x
x
