9788

120

ты затрат этих клеток стали равны нулю, потенциалы 2-й и 4-й строк таблицы должны быть равны (– 4) и 0 соответственно. Тогда для заполненной клетки

(1,4) коэффициент затрат после сложения будет равен 3+1=4, поэтому, чтобы он стал равен нулю, четвертому столбцу надо придать потенциал, равный –4.

Действуя далее аналогично, последовательно получим: потенциал 1 для первой строки, –1 для третьего столбца, –3 для третьей строки и 0 для второго столбца.

Прибавляя полученные потенциалы к коэффициентам затрат (и по строкам, и

по столбцам), получаем следующую матрицу оценок:

Так как среди оценок клеток есть отрицательные, полученное распределе-

ние не является оптимальным. Выберем клетку (произвольно) с отрицательной оценкой, например, (4,4), и построим для нее означенный цикл пересчета. В

цикле, кроме выбранной клетки, должны, участвовать только заполненные клетки, в каждом столбце и в каждой строке цикла должно быть по две клетки.

Для клетки (4,4) цикл пересчета выглядит так:

Найдем максимальное значение поставки, которое можно передвинуть по циклу как наименьшее значение поставки в «отрицательных» клетках. В нашем случае такая поставка равна 30. Заметим, что передвинув по циклу 30 единиц,

получим нулевые поставки сразу в двух клетках – (2,4) и (4,1). Если считать их

121

В матрице нет отрицательных оценок, следовательно, полученное распре-

деление оптимально. Посчитаем суммарные затраты на перевозку этого рас-

пределения поставок.

Fmin 4 50 3 50 5 20 4 20 3 30 620 .

123

5.2. Элементы теории матричных игр

Задача 1. Определить нижнюю и верхнюю цену игры, заданной платежной

Решение. Найдем по каждой строчке платежной матрицы минимальное число αi min(ai1,ai2 ,ai3 ) – это гарантированный выигрыш игрока А при выбо-

ре им соответствующей стратегии. Чтобы получить максимально возможный гарантированный выигрыш, игрок А должен выбрать ту стратегию, для которой

им стратегии B j . Найдем минимальное из этих чисел β min(β1,β2 ,β3 ) – это верхняя цена игры. Занесем полученные данные в таблицу.

седловую точку. Для игрока А оптимальная стратегия – A3 , для игрока В опти-

мальная стратегия – B2 .

Ответ: α β 0 , игра имеет седловую точку, оптимальные стратегии ( A3 , B2 ) .

Задача 2. Решить графически игру, заданную платежной матрицей:

Решение. Дана игра 4 х 2, то есть у игрока А имеется 4 стратегии, а у иг-

рока В – 2. Поэтому будем решать игру для игрока В. Построим оси: ОХ – на ней будем отмечать вероятности, с которыми игрок использует ту или иную стратегии, и ОУ – на ней будем откладывать цену игры. На расстоянии единица от оси ОУ проведем еще ось, параллельную ей (см. рис. 19).

Рис. 19. Графическое решение задачи

Если игрок А выбирает стратегию A1 , то игрок В, используя свои страте-

сколько в среднем получает игрок В, если А использует стратегию A1 , а В чере-

дует стратегии B1 и B2 с некоторыми вероятностями q1, q2 . Аналогично от-

мечаем на оси ОУ точку –2, а на параллельной ей оси – точку 0 и соединяем от-

резком. Получаем линию, показывающую, сколько в среднем получает игрок В,

если А выбрал стратегию A2 . Точно так же для A3 и A4 . Для игрока В надо вы-

брать верхнюю границу, так как он должен рассчитывать, что А выберет ту стратегию, которая соответствует наибольшему проигрышу для игрока В. На рис. 19 это ломаная A3 KA4 , выделенная толстой линией. Игроку В следует вы-

брать ту смешанную стратегию, которая соответствует наименьшему проигры-

шу для В – точка К. Это точка пересечения прямых, соответствующих страте-

гиям A3 и A4 . Выпишем уравнения этих прямых.

125

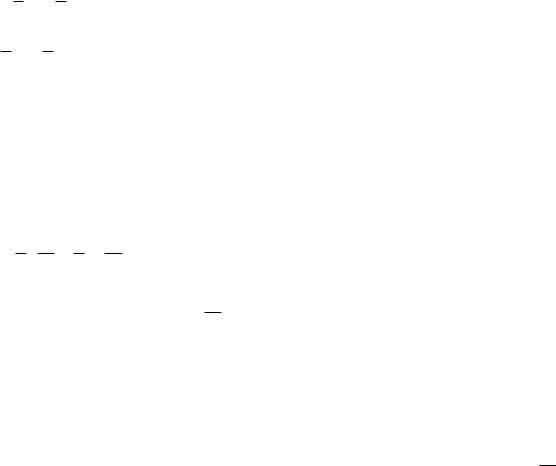
Прямая ( A3 A3 ), проходит через точки с координатами (0; 5) и (1; -2).

Уравнение этой прямой запишется в следующем виде:

Уравнение прямой ( A4 A4 ), проходящей через точки (0; -3) и (1; 3), запишется в следующем виде:

Точка К – точка пересечения этих прямых, имеет координаты, удовлетворяю-

щие системе:

x 17 y 75

x 1 y 16 2

Решаем систему:

Откуда x 16 139 12 138 .

Следовательно, цена игры v 139 и оптимальная стратегия для игрока В:

Для игрока А, стратегии A1 и A2 будут неактивными, игроку А невыгодно

их использовать. Максимально возможный выигрыш, равный цене игры v 139 ,

игрок А будет получать, используя стратегии A3 и A4 .

126

Найдем оптимальную смешанную стратегию для игрока А из следующей

Замечание. Если игра размера 2 х n, то ее следует решать для игрока А. То-

гда на чертеже следует выбирать нижнюю границу и максимальное значении этой границы.

Задача 3. (Сведение матричной игры к задаче линейного

программирования)

Прибавляя ко всем элементам матрицы (Pij ) число k= 5, приходим к мат-

линейного программирования.

127

Воспользовавшись симплекс-методом, находим решение:

В рассматриваемой игре Pij Т Pij и S*A S*В . Нетрудно найти оптималь-

ную смешанную стратегию второго игрока, решив соответствующую задачу линейного программирования, и убедиться в том, что она совпадает с опти-

мальной смешанной стратегией первого игрока.

Завершая рассмотрение игр двух участников с нулевой суммой без седло-

вых точек, заметим, что при использовании смешанных стратегий перед каж-

дой партией игры каждым игроком запускается некий механизм (бросание мо-

неты, игральной кости или использование датчика случайных чисел), обеспечи-

вающий выбор каждой чистой стратегии с заданной вероятностью. Как мы уже отмечали, смешанные стратегии представляют собой математическую модель гибкой тактики, при использовании которой противник не знает заранее, с ка-

кой обстановкой ему придется столкнуться в каждой следующей партии игры.

При этом ожидаемые теоретические результаты игры, при неограниченном воз-

растании числа разыгрываемых партий, стремятся к их истинным значениям.

128

5.3. Принятие решений в условиях неопределённости и риска

Задача 1. Задача о постройке мотеля.

Планируется постройка мотеля. Требуется сделать предварительную оцен-

ку доходности мотеля. Затраты на постройку мотеля для простоты не учитыва-

ются. Проблема заключается в неопределѐнности спроса.

Ежегодные затраты будут зависеть от числа сданных комнат S, от размера мотеля (тоже от числа комнат). Кроме того, будут учтены фиксированные за-

траты. Доходы зависят от числа сданных комнат R.

Составление сметы доходов даѐт следующую таблицу:

Решение

Величина в скобках – сожаление между наиболее благоприятным и дейст-

вительным выбором.

Коэффициент оптимизма α.

В данном случае M=6.

Решение по Лапласу S=40. Если все события равновероятны.

Решение по Вальду S=20. В этом случае можно гарантировать, что убыток не превосходит 121.

129