
9778
.pdf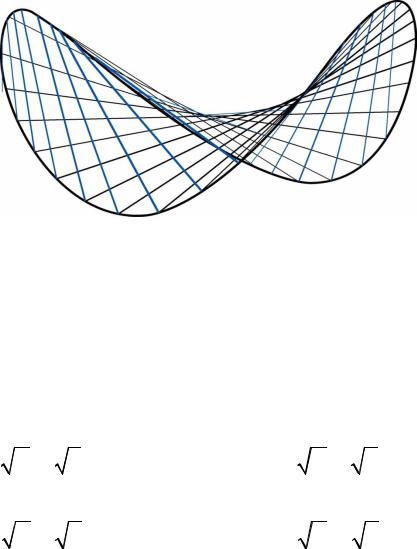
Поверхность гиперболического параболоида можно также
получить «механическим» образом. Пусть одна парабола
расположена в плоскости xOz , а другая |
парабола z = − y2 – в |
перпендикулярной ей плоскости yOz . |
«Заставим» теперь |
нижнюю параболу скользить вершиной по верхней параболе,
перемещаясь параллельно плоскости yOz . Эта скользящая
парабола и образует гиперболический параболоид.
Интересно, что гиперболический параболоид, как и однополостный гиперболоид, является линейчатой поверхностью
– его можно сформировать из прямых (рис. 8.8).
Рис. 8.8
Гиперболический параболоид с уравнением (8.6) имеет две системы прямолинейных образующих, определяемых уравнениями
α |
|
x |
+ |
z |
|
|
= 2β z, |
|
α |
|
x |
|
|
− |
y |
|
|
|
= 2β z, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
q |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
z |
|
|
|
|
x |
|
|
|
z |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
β |
|
|
|
− |
|
|
|
|
= α. |
|
|
β |
|
|
|
+ |
|
|
|
|
|
= α. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
q |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Завершим обзор поверхностей второго порядка полной их классификацией. Всякое уравнение второго порядка в пространстве с помощью подходящего параллельного переноса и поворота осей координат может быть приведено к одному из видов, соответствующих рассмотренным поверхностям:
|
|
x |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
||||||||||||
1) |
|
|
+ |
|
|
|
|
|
|
y |
+ |
|
|
|
|
|
|
|
|
|
= 1 |
(эллипсоид) |
|||||||||||||
|
a |
2 |
2 |
|
|
|
|
|
c |
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|||||||||||||
2) |
|
|
|
|
|
|
|
+ |
|
|
y |
|
|
|
+ |
|
|
|
|
|
|
|
= 0 |
(точка) |
|||||||||||
|
a |
2 |
|
2 |
|
|
|
|
c |
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
2 |
2 |
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|||||||||||||||
3) |
|
|
|
|
|
|
|
|
+ |
|
y |
|
|
|
|
|
+ |
|
|
|
|
|
|
= −1 (мнимый эллипсоид) |
|||||||||||
|
a |
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|||||
|
|
x |
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
4) |
|
|
|
|
+ |
|
|
y |
|
|
|
|
− |
|
|
z |
|
|
|
= 1 |
(однополостный гиперболоид) |
||||||||||||||
|
a |
2 |
|
|
2 |
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
c |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
x |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
5) |
|
|
|
|
|
|
|
+ |
y |
|
|
− |
z |
|
|
= −1 (двуполостный гиперболоид) |
|||||||||||||||||||
|
a |
2 |
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
||||||||
|
|
x |
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
6) |
|
|
|
|
|
+ |
|
y |
|
|
|
− |
z |
|
|
= 0 |
(конус) |
||||||||||||||||||
|
a |
2 |
|
|
|
2 |
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|||||||||
7) |
2z = |
x2 |
|
|
|
+ |
y2 |
|
|
|
(эллиптический параболоид) |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|||||||
2 2
8)2z = p q (гиперболический параболоид)
9)- 17) уравнения кривых второго порядка задают в пространстве девять видов цилиндров второго порядка.− yx
Построение тел, ограниченных
несколькими поверхностями
Наиболее интересные задачи, связанные с разобранными вопросами, - это получение формы тел, ограниченных несколькими поверхностями.
81
Пример. Построить тело, сформированное двумя поверхностями, заданными уравнениями
|
|
x2 |
+ |
y2 |
+ |
z2 |
= 1 |
(8.7) |
|
9 |
|
|
|||||
|
4 |
4 |
|
|
||||
и |
x = 0, 9( y2 + z2 ) . |
(8.8) |
||||||
Решение. |
Уравнение (8.7) |
определяет |
в пространстве |
|||||
эллипсоид вращения с полуосями a = 3, b = c = 2 . Его общий вид
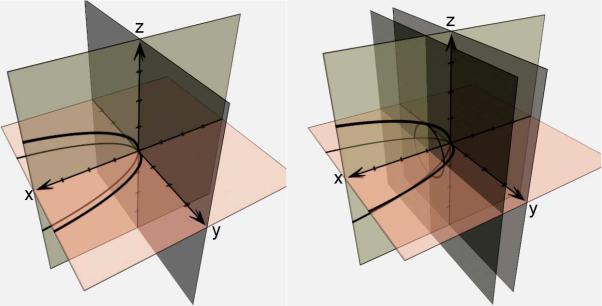
изображен на рисунке 7.5. Уравнение (8.8) задаёт параболоид вращения, который, в отличие от изображённого на рисунке 8.6,
симметричен относительно оси Ox . Здесь параболы получаются в сечениях координатными плоскостями xOz и xOy (рис. 8.9), а
в сечениях плоскостями x = h , если h > 0 - окружности (рис. 8.10).
Рис. 8.9 |
Рис. 8.10 |
Поскольку ось Ox |
является осью вращения и для |
эллипсоида, то его сечение плоскостями x = h , если h > 0 , тоже являются окружностями. Можно найти значение h , при котором
82
радиусы окружностей параболоида и эллипсоида совпадут, то есть поверхности пересекутся. Для этого выразим из (8.8)
y2 + z2 = |
10 |
x |
и подставим в (8.7): 2x2 + 5x −18 = 0 . Из двух |
|
|||
9 |
|
|
|
решений квадратного уравнения оставляем положительное x = 2 .
Итак, эллипсоид и параболоид пересекутся при x = 2 по
окружности с уравнением |
y2 + z2 = |
20 |
. |
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
9 |
|
|
|
|
||
Можно |
изобразить |
пересечение |
поверхностей |
в |
||||||
координатной |
плоскости |
xOz (рис. 8.11) |
– это парабола |
с |
||||||
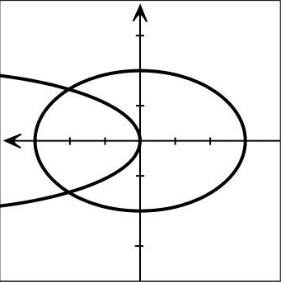
уравнением x = 0,9z2 и эллипс |
x2 |
+ |
z2 |
= 1. |
|
|
||||
|
|
|
|
|
||||||
9 |
4 |
|
|
|||||||
Рис. 8.11
Обе поверхности можно теперь построить в одних координатных осях (рис. 8.12) и изобразить вид тела, ими ограниченного (рис. 8.13).
83
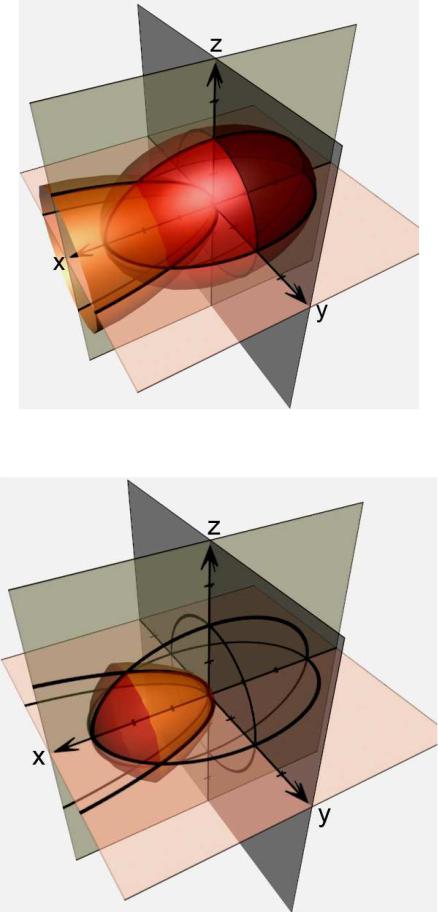
Рис. 8.12
Рис. 8.13
84
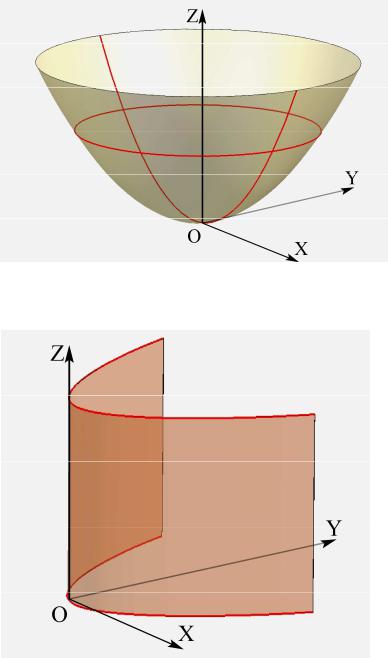
Пример. |
Построить тело, ограниченное параболоидом |
|
вращения с |
уравнением |
4z = x2 + y2 , параболическим |
цилиндром с уравнением y = 0,5x2 , координатной плоскостью xOy , а также плоскостью y = 2 .
Решение. Как обычно, формируем сечениями указанные поверхности: рис. 8.14, рис. 8.15.
Рис. 8.14
Рис. 8.15
85

Рис. 8.16
При стыковке поверхностей прорисовывается тело (рис.
8.16), форму которого можно уточнить, рассмотрев сечение
плоскостями |
z = 0 |
и |
y = 2 . |
Заметим, что точки M (2; 2;0) , |
||
N (−2; 2;0) и |
P(0; 2; 0) |
являются проекциями на плоскость xOy |
||||
′ |
|
|
′ |
|
′ |
принадлежащих |
точек M (2; 2;2) , |
N (−2; 2; 2) |
и P (0; 2;1) , |
||||
параболоиду (рис. 8.17).
Рис. 8.17
86
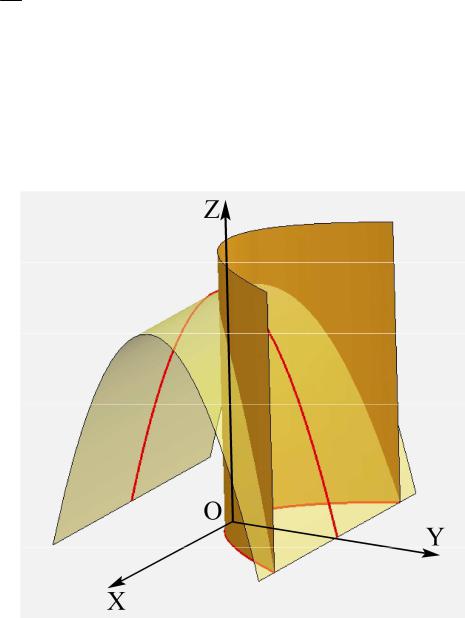
Пример. |
Получить форму тела, ограниченного двумя |
параболическими |
цилиндрами с уравнениями z = 4 − y2 и |
y = x2 , срезанными координатной плоскостью xOy .
2
Решение. Образующие первого цилиндра параллельны оси
Ox , второго – оси Oz . Изобразим для начала параболы,
получающиеся в сечениях цилиндров координатными плоскостями (рис. 8.18).
Рис. 8.18 |
|
|
|
|
В координатной плоскости xOy парабола |
y = |
x2 |
срезается |
|
|
||||
|
|
2 |
|
|
прямой x = 2 , завершаясь точками M (2; 2;0) |
и N (−2; 2;0) . В |
|||
координатной плоскости yOz в |
сечении получающегося тела |
|||
остаётся часть параболы z = 4 − y2 |
от вершины K (0;0; 4) до точки |
|||
P(0; 2;0) . |
|
|
|
|
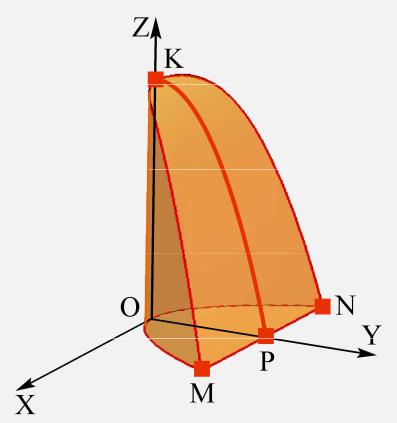
Окончательную форму тела изображаем рисунком 8.19.
Рис. 8.19
Рассмотрение примеров построения тел, ограниченных заданными поверхностями, синтезирует изложенные теоретические вопросы аналитической геометрии с умением их использовать для получения требуемых пространственных форм.
88
Библиографический список
1. Данко, П. Е. Высшая математика в упражнениях и задачах. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Е. Кожевникова. –
Москва : Мир и образование, 2008. – 368 с.
2. Протасова, Л. А. От геометрии – к дизайн-проекту, или Как я полюбил математику : учеб. пособие для вузов / Л. А.
Протасова, А. А. Бутысин ; Нижегор. гос. архитектур.-строит. ун-
т. – Нижний Новгород : ННГАСУ, 2013. – 137 с.
3. Пучков, Н. П. Математика в архитектуре : учеб.-метод.
рекомендации к изучению теорет. части курса «Математика» студентам специальности 290100 / Н. П. Пучков, Т. В.
Четвертнова ; Тамб. гос. техн. ун-т. – Тамбов : ТГТУ, 2001. – 40 с. 4. 64 лекции по математике : учеб. пособие. Кн. 1 : (лекции
1-39) / В. П. Важдаев, М. М. Коган, М. И. Лиогонький Л. А.
Протасова ; Нижегор. гос. архитектур.-строит. ун-т. – Нижний Новгород : ННГАСУ, 2012. – 286 с. : ил.
89
