
9774
.pdf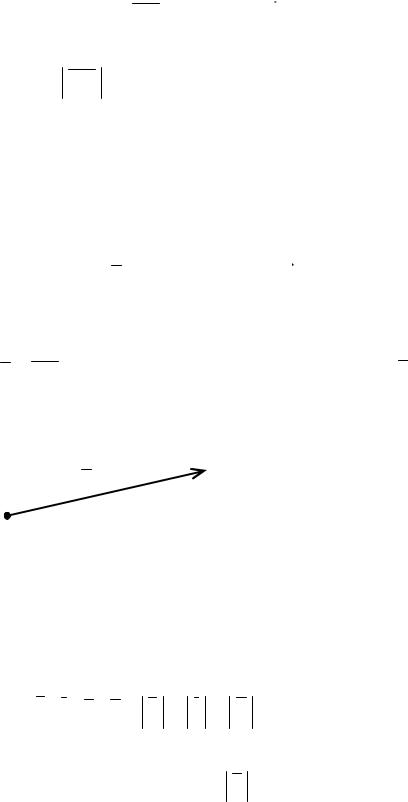
§ 2. Векторная алгебра
Обобщим некоторые сведения о векторах, известные в основном из школьного курса геометрии.
Закрепленным вектором AB (или AB ) называется направленный отрезок, у которого выделено начало A и конец
B . Длиной вектора AB называется длина отрезка,
изображающего данный вектор.
Два закрепленных вектора называются эквивалентными,
если у них совпадают длина и направление. Множество эквивалентных закрепленных векторов называется свободным вектором. Свободные векторы обозначают маленькими буквами латинского алфавита (например, a или со стрелкой a ).
Свободный вектор можно переносить параллельно самому себе, и его началом можно считать любую точку пространства.
Тем самым, запись a = AB означает, что свободный вектор a
откладывается от точки A (рис. 2.1).
B
a
A
Рис. 2.1
В векторной алгебре всегда имеют дело со свободными векторами (далее – просто векторами).
Назовем вектор ортом, если его длина в заданном масштабе равна единице. Для обозначения единичных векторов, или ортов,
чаще используют буквы e, i , j , k ( e = i = j = 1).
Нуль-вектором называется вектор, начало и конец которого совпадают. Он имеет нулевую длину, то есть 0 = 0 .
10
Линейные операции над векторами
Линейными операциями над векторами называются операции сложения векторов и умножение вектора на число.
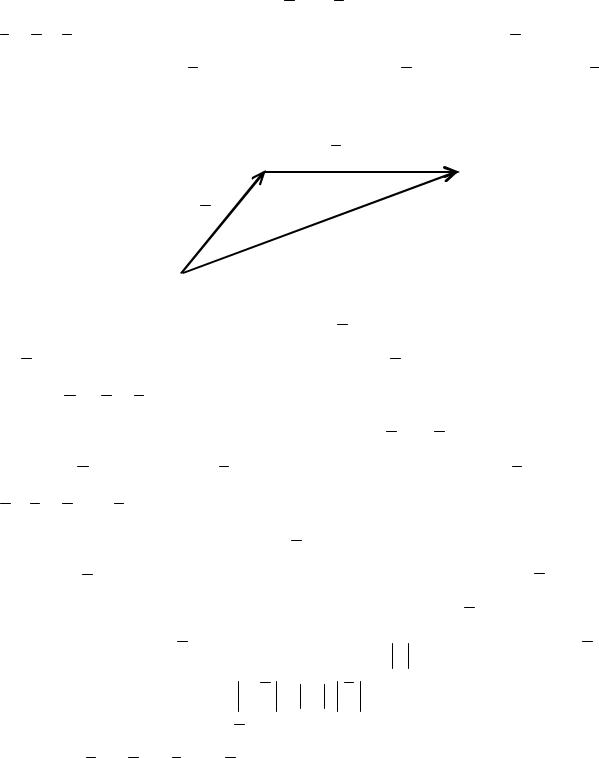
Суммой двух векторов a и b называется третий вектор c = a + b , начало которого совпадает с началом вектора a , а конец
– с концом вектора b , если конец вектора a и начало вектора b
совмещаются (рис. 2.2).
b
a |
|
+ |
|
|
a |
b |
Рис. 2.2
Противоположным вектору a называется такой вектор
(− a), который при сложении с вектором a дает нуль-вектор, то есть (- a)+ a = 0 .
Заметим, что разностью векторов a и b является сумма вектора a и вектора (− b), противоположного вектору b , то есть a − b = a + (− b).
Произведением вектора a на число λ называется такой вектор λa , направление которого совпадает с вектором a , если
λ > 0 и противоположно направлению вектора a , если λ < 0 ;
длина же вектора λa равна произведению λ на длину вектора a :
λ a = λ × a .
Пусть дан вектор a (рис. 2.3). Изобразим для примера векторы b = 2a и c = -3a :
11
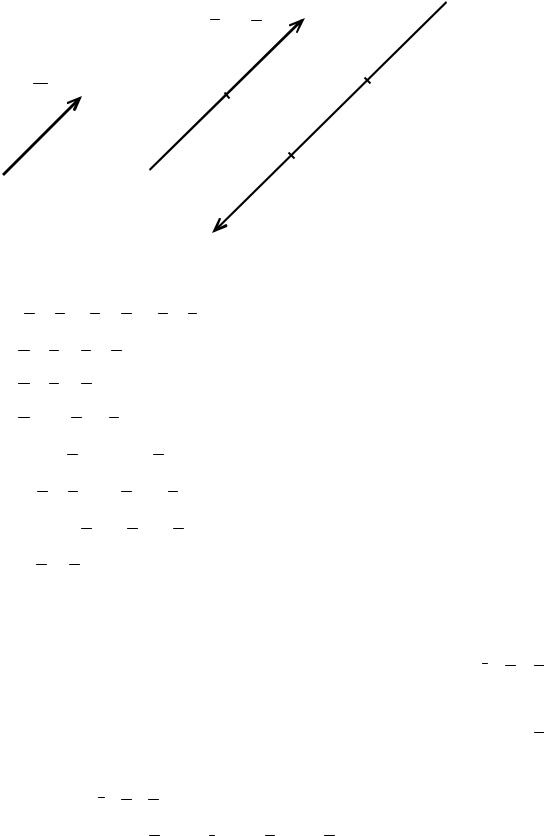
b = 2a
a
|
= −3 |
|
|
|
c |
a |
Рис. 2.3 |
Свойства линейных операций над векторами
1.(a + b)+ c = a + (b + c)
2.a + b = b + a
3.a + 0 = a
4.a + (- a)= 0
5.α × (β a)= (α β )a
6.λ(a + b)= λ a + λ b
7.(λ + μ )a = λ a + μ a
8.1× a = a , где α , β , λ , μ – действительные числа.
Действия над векторами в координатной форме
Три единичных взаимно перпендикулярных вектора i , j , k
пространства называются базисными векторами или
декартовым базисом пространства. Любой вектор a
пространства может быть единственным образом разложен по
векторам базиса i , j , k (рис. 2.4):
a = a1 ×i + a2 × j + a3 × k .
12
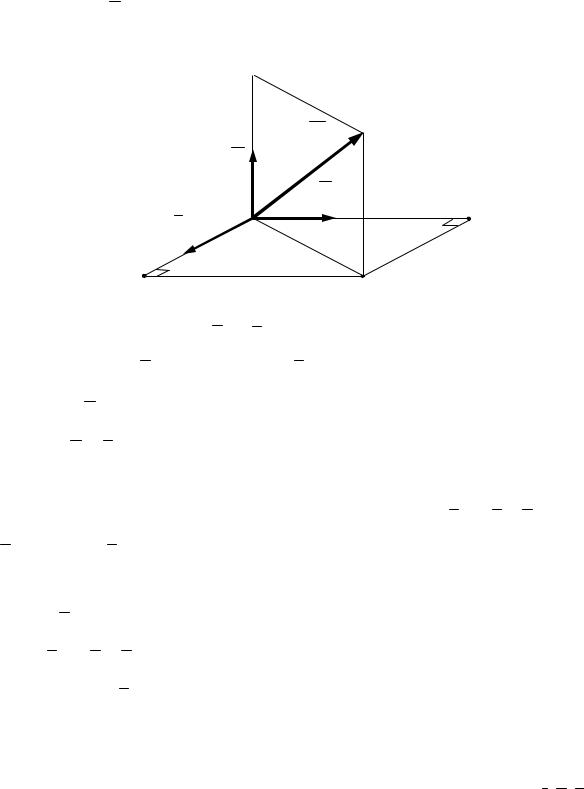
Коэффициенты {a1 , a2 , a3} разложения вектора по базису называются его координатами. Коротко это записывают равенством a = {a1 , a2 , a3 }.
a3

a
k
j |
a2 |
i
a1
Рис.2.4
Если два вектора a и b в декартовом базисе заданы своими координатами a = { a1, a2 , a3} и b = {b1 , b2 , b3 }, то
1)λ a = {λ a1 , λ a2 , λ a3 };
2)a + b = {a1 + b1 ; a2 + b2 ; a3 + b3}.
Пример. Найти координаты вектора c = 2a + b , если a = {1; 2;3}, b = {−1; 0;1}.
Решение:
2a = {2 ×1; 2 × 2; 2 ×3}= {2; 4; 6}.
c = 2a + b = {2; 4; 6}+ {−1; 0;1}= {2 + (−1); 4 + 0; 6 +1} = {1; 4; 7}.
Ответ: c = {1; 4; 7}.
Прямоугольной декартовой системой координат в
пространстве называется совокупность точки O и базиса (i, j, k ).
Точка O называется началом координат, оси Ox , Oy и Oz ,
проходящие через начало координат в направлении базисных
13
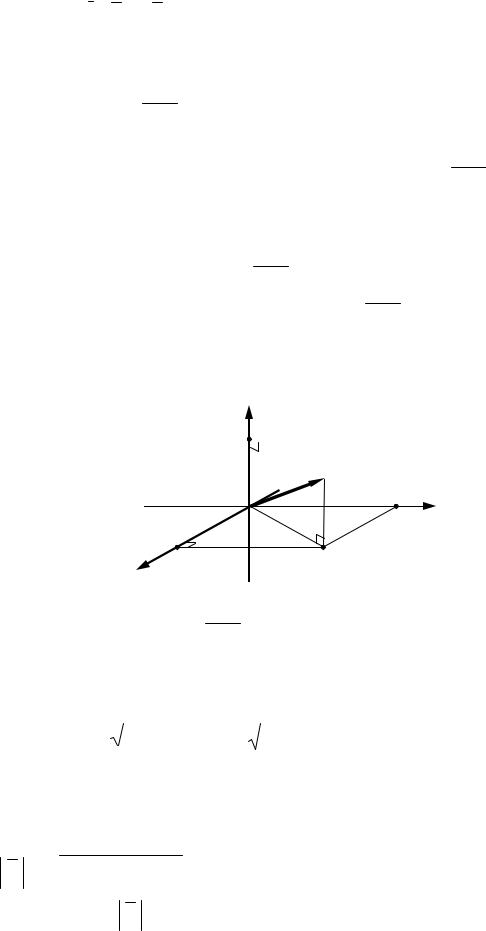
векторов i , j и k называются осями координат. Плоскости xOy , xOz и yOz , проходящие через каждую пару осей координат,
называются координатными плоскостями.
Вектор OM , соединяющий начало координат и произвольную точку M пространства, называется радиус-
вектором точки M . Координаты радиус-вектора OM называются координатами точки M в прямоугольной декартовой системе координат. Тем самым, обозначение координат точки M (x; y; z)
соответствует равенству OM = {x; y; z}, то есть координатами точки M являются проекции вектора OM на оси Ox , Oy и Oz
соответственно (рис. 2.5)
z
 M
M
|
O |
|
B |
A |
|
x |
||
|
 y
y
Рис. 2.5
Длина вектора OM |
находится из двух |
прямоугольных |
||||||||||||||||||||||
треугольников |
OBA и OAM : |
|
||||||||||||||||||||||
OA2 = OB2 + AB2 = x2 + y2 ; |
|
|||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|
|
|||
|
OM |
|
OA2 + AM 2 |
x2 + y2 + z 2 |
|
|||||||||||||||||||
|
|
|
, если |
|
|
= |
|
− 2 |
|
+ 2 |
|
. |
|
|||||||||||
Пример. Найти |
|
a |
|
a |
i |
j |
k |
|
||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
= {1;−2; 2}, то |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
Поскольку |
|
|
a |
длина вектора |
||||||||||||||||||||
a = 
 12 + (− 2)2 + 22 = 3.
12 + (− 2)2 + 22 = 3.
Ответ: a = 3.
14

Если для |
вектора AB известны |
координаты |
его начала |
|||||||
A(x1; y1; z1) и |
конца B(x2; y2; z2 ), |
то |
можно |
найти его |
||||||
координаты, |
учитывая, |
|
|
|
= |
|
- |
|
: |
|
что |
|
AB |
OB |
OA |
||||||
AB = {x2 - x1; y2 - y1; z2 - z1} .
Пример. Найти координаты вектора AB , если A(1;2;3) ,
B(−1;0;1) .
Решение:
AB = {-1-1;0 - 2;1- 3} = {-2;- 2;- 2} .
Ответ: AB = {−2;− 2;− 2}.
Скалярное произведение векторов
Скалярным произведением a ×b двух ненулевых векторов
a и b называется число, равное произведению длин этих
векторов на косинус угла между ними: a ×b = a × b × cos (a b) .
Свойства скалярного произведения
1)a ×b = b × a ;
2)(λ a)×b = λ(a ×b), λ R ;
3)a × (b + c)= a ×b + a × c ;
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) a × a = |
|
a |
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
× |
|
. |
|
|
|
|
|
|
(2.1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
a |
a |
a |
||||||||||||||||||||
Пример. |
|
|
|
|
|
= |
|
+ 2 |
|
, если |
|
|
|
|
= 2 , |
|||||||||||||||
|
Найти |
|
длину вектора |
c |
a |
b |
|
a |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b =1, a b = 60O .
15

Решение. По формуле (2.1), находим
c = 
 c × c =
c × c = 
 (a + 2b)× (a + 2b) =
(a + 2b)× (a + 2b) = 

 a 2 + 4a b + 4 b 2 =
a 2 + 4a b + 4 b 2 =
= 22 + 4 a × b × cos a b+ 4 ×12 = 
 4 + 4 × 2 ×1× cos 60O + 4 =
4 + 4 × 2 ×1× cos 60O + 4 =
=
 8 + 8 × 1 =
8 + 8 × 1 = 
 12 = 2
12 = 2
 3 .
3 .
 2
2
Ответ: c = 2
 3 .
3 .
|
|
Если два |
вектора a и b |
заданы своими |
координатами |
||||||||
|
|
= {a1; a2 ; a3 } |
|
|
|
|
|
|
= {b1 ;b2 ;b3 }, |
|
|
|
|
|
a |
и |
b |
то их скалярное |
произведение |
||||||||
находим по формуле |
|
|
|
|
|||||||||
|
|
|
|
|
× |
|
= a1 ×b1 + a2b2 + a3b3 . |
|
|
|
|||
|
|
|
|
a |
b |
(2.2) |
|||||||
|
|
Пример. |
|
|
|||||||||
|
|
Найти скалярное |
произведение векторов 2 |
a |
и |
||||||||
(- 3b), если a = {1; 2;3} и b = {0;-1;1}.
Решение. Координаты векторов 2a и (- 3b)
2a = 2{1; 2;3} = {2 ×1; 2 × 2; 2 ×3} = {2; 4; 6};
(- 3b)= -3{0;-1;1} = {- 3 × 0;-3 ×(-1);-3 ×1} = {0;3;-3}.
По формуле (2.2) искомое скалярное произведение равно
2a × (- 3b)= 2 × 0 + 4 ×3 + 6 × (- 3) = 0 +12 -18 = -6.
Ответ: − 6 .
Некоторые приложения скалярного произведения
1. Угол между двумя ненулевыми векторами a = {a1; a2 ; a3 } и b = {b1 ; b2 ; b3 } из определения скалярного произведения вычисляется по формуле
16
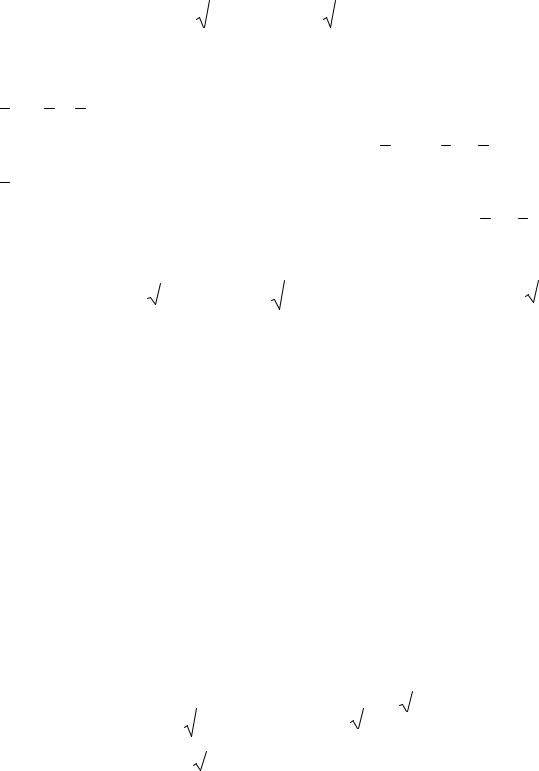
|
|
|
|
|
|
|
|
|
|
|
|
a ×b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( |
|
|
|
|
|
) = arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
b |
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a1b1 + a2b2 |
+ a3b3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(a b) = arccos |
|
|
|
|
|
|
|
(2.3) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a2 |
+ a2 |
+ a2 |
× |
|
|
|
b2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ b2 + b2 |
|||||||||||||||||||||||||
1 |
2 |
3 |
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пример. Найти угол между векторами |
|
|
|
|
= |
|
+ 2 |
|
+ 2 |
|
и |
||||||||||||||||||||||||||
|
|
a |
i |
j |
k |
||||||||||||||||||||||||||||||||
b = - j + k .
Решение. Координаты векторов a и b : a = {1; 2; 2} и b = {0;-1;1}.
Тогда по формуле (2.3), угол между векторами a и b равен:
|
|
|
|
|
1×0 + 2 ×(-1) + 2 ×1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 -1+ 2 |
|
||||||||||||||||||||||||||||||||||||||||||||
( |
a |
|
b |
) = arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= arccos |
3× |
|
|
|
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
)2 |
|
|
|
|
|
0 |
||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
+ |
2 |
2 |
× |
0 |
2 |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 + 2 |
|
|
|
+ - |
1 |
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
= arccos 0 , следовательно, ( |
a |
|
b |
) = 90O , то есть |
a |
^ |
b |
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Ответ: 90O . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2. Проекция вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
a |
|
на вектор |
b |
|
вычисляется по формуле |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
× |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
np |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
+ |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Пример. Найти |
|
|
|
|
|
|
|
|
= |
|
- |
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
np |
|
|
|
b |
, если |
|
|
a |
i |
k |
и |
b |
i |
j |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
= {1; 0;-1}, |
|
|
|
= {2;1; 0}. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Координаты векторов |
|
|
|
|
|
|
a |
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда
|
|
|
|
= |
|
|
|
× |
|
|
|
|
|
= |
|
1× 2 + 0 ×1 + (-1)× |
0 |
= |
2 |
|
= |
|
. |
|||||||
|
|
|
|
a |
b |
|||||||||||||||||||||||||
np |
|
|
b |
|
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a |
|
|
a |
|
|
|
|
|
|
|
12 + 02 + (-1)2 |
2 |
|
|
|
|
|||||||||||||
Ответ: |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
np |
|
|
|
b |
2 . |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
17
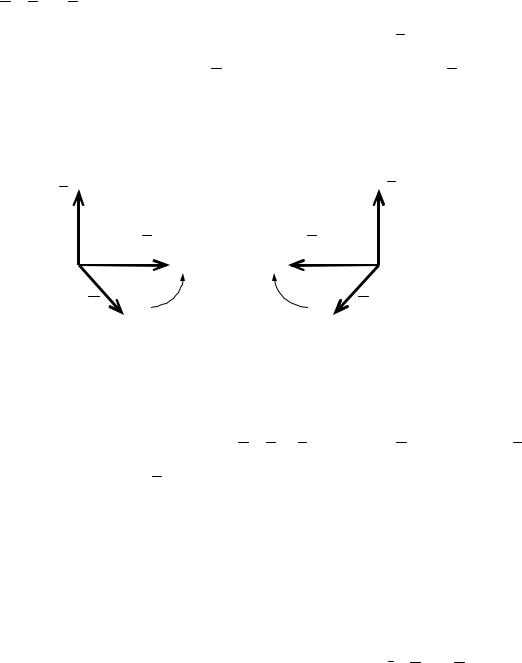
Векторное произведение векторов
Три некомпланарных (непараллельных одной плоскости)
вектора a , b и c , взятые в указанном порядке, образуют правую тройку векторов, если из конца третьего вектора c кратчайший
поворот от первого вектора a ко второму вектору b виден происходящим против хода часовой стрелки (и левую, если по часовой) (рис. 2.6)
c |
c |
b |
b |
a |
a |
правая |
левая |
|
|
тройка |
тройка |
|
|
|
Рис.2.6 |
Векторным произведением a ´ b = c вектора a на вектор b
называется такой вектор c , что
1) |
|
|
|
|
^ |
|
, |
|
|
|
^ |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
||||||
|
c |
a |
c |
b |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
× |
|
|
|
|
×sin |
|
|||||||||||||
2) |
|
|
|
c |
|
|
a |
|
|
b |
|
a |
|
|
b |
; |
|
|
|
|
|||||||||||
3) |
|
|
, и |
|
– правая. |
||||||||||||||||||||||||||
тройка векторов |
a |
, |
b |
c |
|||||||||||||||||||||||||||
Из определения векторного произведения непосредственно
вытекают следующие соотношения между ортами i , j , и k :
|
|
´ |
|
= |
|
, |
|
|
´ |
|
= |
|
|
|
, |
|
|
|
|
|
|
´ |
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||
i |
j |
k |
j |
k |
i |
k |
i |
|
j |
||||||||||||||||||||||||||||||||||||||||||||
Поскольку тройки векторов ( |
|
|
, |
|
, |
|
|
|
), |
( |
|
|
, |
|
|
, |
|
) и ( |
|
, |
|
, |
|
) левые, |
|||||||||||||||||||||||||||||
|
j |
i |
k |
k |
j |
i |
i |
k |
j |
||||||||||||||||||||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
´ |
|
= - |
|
, |
|
|
|
´ |
|
= - |
|
, |
|
|
|
´ |
|
= - |
|
. |
||||||||||||||||||||||||||||||
|
|
j |
i |
k |
|
k |
j |
i |
|
i |
k |
j |
|||||||||||||||||||||||||||||||||||||||||
18

Свойства векторного произведения
1)a × b = −(b × a);
2)c × (a + b)= c × a + c × b ;
3)λ(a ´ b)= (λ a)´ b = a ´ (λb), λ R ;
4)a ´ b = 0 a || b .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторов |
|
|
|
= {a1; a2 ; a3 } и |
||||||||
|
|
Векторное |
произведение |
|
двух |
a |
|||||||||||||||||||||||
|
|
= {b1 ; b2 ; b3 } находится по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
´ |
|
= |
|
a2 |
a3 |
|
× |
|
- |
|
a1 |
a3 |
|
× |
|
+ |
|
a1 |
a2 |
|
× |
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
a |
b |
i |
j |
k |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
b2 |
b3 |
|
|
|
|
|
b1 |
b3 |
|
|
|
|
|
b1 |
b2 |
|
|
|
|
||
|
|
Пример. |
Найти |
векторное |
|
|
|
произведение векторов |
|||||||||||||||||||||
a = {1; 2;3} и b = {0;1;-1}.
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
3 |
|
|
|
|
|
1 |
3 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a ´ b = |
×i - |
× j + |
× k = |
|||||||||||||||||||||
1 |
-1 |
|
|
0 |
-1 |
|
|
0 |
1 |
|||||||||||||||
= (- 2 - 3)×i - (-1 - 0)× j + (1 - 0)× k = - 5i + j + k .
Ответ: a ´ b = - 5i + j + k .
Геометрический смысл векторного произведения состоит в том, что площадь параллелограмма, построенного на векторах
a и b (рис. 2.7) равна модулю векторного произведения векторов a и b , так как
a ´b = a × b ×sin α = Sпарал. .
b
α
a Рис. 2.7
19
