9772

Гипербола

Множество всех точек M плоскости, разность расстояний

которых до двух данных точек F1 и F2 есть величина постоянная,

называется гиперболой. Указанная разность берётся по абсолютному значению и обозначается 2a . Точки F1 и F2

чтобы фокусы F1 и F2 лежали на оси Ox , а начало координат совпадало с серединой отрезка F1F2 (рис. 5.2). В этой системе координаты произвольной точки M обозначим x и y , а

координаты фокусов будут соответственно: F1 (−c;0) , F2 (c;0) .

Заменив расстояние F1M и F2 M между точками их выражениями через координаты, получим

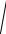( x + c)2 + y2 − 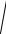( x − c)2 + y2 = ±2a .

Это уравнение, как и для эллипса, приводится для удобства к другому виду. Перенесём второй радикал в правую часть и возведём в квадрат обе части уравнения

( x + c)2 + y2 = 4a2 ± 4a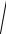( x − c)2 + y2 + ( x − c)2 + y2 ,

раскроем скобки и после сокращения получим

xc − a2 = ±a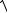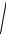( x − c)2 + y2 .

50

Снова возводим в квадрат и сокращаем подобные слагаемые:

чётных степенях, то гипербола симметрична относительно осей

Ox и Oy , а также относительно начала координат. Оси

симметрии гиперболы называются её осями, а точка пересечения осей – центром гиперболы.

Положив y = 0 в уравнении (5.3), найдём две точки пересечения гиперболы с осью Ox : A1 (-a;0) , A2 (a;0), которые называются вершинами гиперболы. Если взять x = 0 в уравнении

Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы (рис. 5.2).

Из уравнения (5.3) следует, что если x < a , то y не имеет

действительных значений, то есть, нет точек гиперболы с

2

абсциссами −a < x < a . Должно выполняться условие x2 ³1 или a

51

x ³ a . Это означает, что гипербола состоит из двух частей: её точки расположены справа от прямой x = a , образуя правую ветвь, и слева от прямой x = −a , образуя левую ветвь. Наконец,

x → −∞ от значения x = −a получается левая неограниченная ветвь гиперболы (рис. 5.2).

Рис. 5.2

Присмотримся внимательнее к тому, как точка M «уходит в бесконечность». В математическом анализе используется понятие асимптотического приближения какой-либо кривой Г к

прямой l , называемой асимптотой этой кривой. Это понятие вводится, если возможно неограниченное удаление точки M по бесконечной ветви линии Г , при котором расстояние от точки

52

данной кривой до этой прямой стремится к нулю. Для обеих ветвей гиперболы при x → +∞ и x → −∞ наклонными

асимптотами являются прямые y = ± b x . a

Итак, построение гиперболы по каноническому уравнению

(5.3) следует начинать с изображения основного прямоугольника,

продолжая диагонали которого мы получим асимптоты. Обе бесконечные ветви рисуем неограниченно приближающимися к

x2 − y2 = a2 . Основной прямоугольник равносторонней гиперболы

становится квадратом; прямые y = x и y = −x являются

асимптотами, перпендикулярными друг к другу.

Отношение расстояния между фокусами к расстоянию между вершинами гиперболы называется эксцентриситетом

гиперболы и обозначается буквой ε : ε = c . Для гиперболы ε > 1,

эксцентриситет гиперболы определяется отношением её осей. Он характеризует форму основного прямоугольника гиперболы. Чем

b

меньше эксцентриситет, тем меньше отношение a , то есть

основной прямоугольник более вытянут в направлении действительной оси. Для равносторонней гиперболы ε = 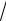2 .

53

Парабола

Множество всех точек плоскости, равноудалённых от данной

точки F (фокуса) и данной прямой L (директрисы), называется

параболой. Расстояние от фокуса до директрисы параболы

принято обозначать через p (рис. 5.3). Величину p называют

фокальным параметром параболы.

Для получения уравнения параболы необходимо ввести систему координат на плоскости. Проведём ось абсцисс через фокус параболы перпендикулярно директрисе, будем считать её направленной от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис. 5.3).

Рис. 5.3

Координаты произвольной точки M параболы обозначим x

перпендикуляра, опущенного из M на директрису. Поскольку Q

54

является частным случаем уравнения второго порядка. Оно

получается из (5.1) при

Уравнение (5.4) содержит переменную y только в чётной

степени, что доказывает симметрию параболы относительно оси

Ox . Так как p > 0 , то переменная x должна быть

неотрицательной. Это означает, что парабола расположена справа

симметрично относительно оси Ox , получим геометрическое изображение параболы (рис. 5.3). Ось симметрии параболы (в

данном случае совпадающая с осью Ox ) называется её осью.

Точка, в которой парабола пересекает свою ось, называется её

вершиной (в нашем случае вершина совпадает с началом координат).

области, ограниченной параболой.

Кроме рассмотренных классических кривых, уравнение линии второго порядка может привести ещё к нескольким

геометрическим случаям, называемым вырожденными.

Вырожденные случаи

Если в уравнении линии второго порядка (5.1)

A > 0,С > 0, F > 0 , то опять ему не удовлетворяют координаты ни одной точки плоскости.

56

§6. Приведение уравнения линии второго порядка к

каноническому виду

Мы рассмотрели все геометрические ситуации, к которым может привести общее уравнение линии второго порядка (5.1). В

задачах аналитической геометрии обычно задаётся вид

уравнения второго порядка с конкретными числовыми коэффициентами. В нём могут присутствовать произведение координат x и y (т.е. B ¹ 0 ) или переменные x и y без

квадратов ( D ¹ 0 или Е ¹ 0 ). Это будет означать, что в исходной системе координат уравнение не является каноническим. Нужно перейти к другой системе координат, в которой уравнение будет иметь канонический вид. Это даст возможность определить, к

какому из рассмотренных случаев относится заданное уравнение.

После этого легко будет построить график заданной кривой.

Для приведения уравнения линии второго порядка к каноническому виду используются только те преобразования

системы координат, которые не изменяют расстояния между

точками, то есть не деформируют кривую. К таким преобразованиям, в частности, относятся параллельный перенос и поворот осей координат. Разберём далее, что происходит с уравнениями при параллельном переносе координат.

Параллельный перенос осей координат

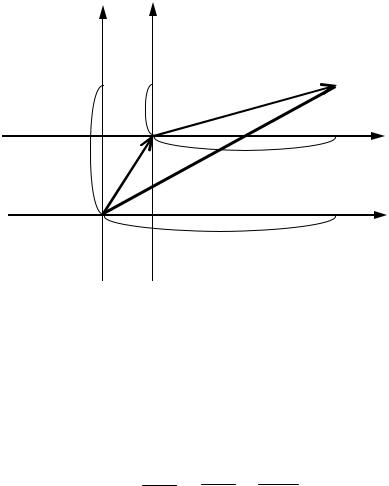
Рассмотрим на плоскости прямоугольную декартову систему координат xOy . Выберем начало вспомогательной системы координат в точке Oў(x0 ; y0 ). Оси Oўxў и Oўyў расположим

параллельно соответствующим осям Ox и Oy , одинаково с ними направив. Масштаб сохраняем. Такой переход от системы xOy к системе Oўxўyў называется параллельным переносом осей координат.

57

Рис. 6.1

Для произвольной точки M координаты относительно

исходных осей обозначим через (x; y), а координаты по отношению к «новым» осям обозначим (xў; yў). Поскольку имеет

место векторное равенство OM = OOў+ OўM (рис. 6.1), то можно записать в координатах

Пример. Какой вид приобретёт уравнение прямой y = 3x - 1

в новой системе координат, если совершается параллельный перенос осей координат к новому началу Oў(1;2)?

58

Видим, что после параллельного переноса уравнение может упроститься (а может и усложниться). Важно правильно выбирать новое начало координат.

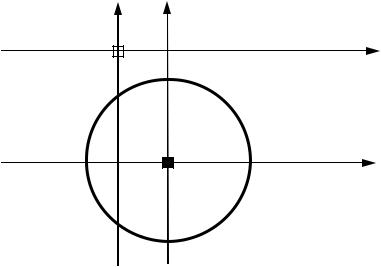
Пример. Привести к каноническому виду уравнение

(x - 1)2 + (y + 3)2 = 4 . Построить кривую, заданную этим

уравнением.

Решение. Ясно, что полезен параллельный перенос

м

пп xў= x- 1 .

н

ппyў= y + 3

о

Уравнение xў2 + yў2 = 4 определяет окружность радиуса 2 с

центром в начале координат Oў(1;- 3). На рисунке 6.2 отражено

построение, соответствующее такому преобразованию.

Ответ: xў2 + yў2 = 4.

y y′

Рис. 6.2

59