
9772
.pdf
Пример. Построить прямую l : 2x − 6 y = 0 .
Решение. Здесь A = 2 , B = −6 , C = 0. Уравнение прямой l
является общим уравнением прямой на плоскости, проходящей
|
|
|
1 |
|
|
через точку O и точку M |
|
1; |
|
|
(рис. 3.7). |
|
3 |
||||
|
0 |
|
|
||
y
l
1 |
M0 |
3 |
1 x |
0 |
Рис.3.7
3. При A = 0 , |
B ¹ 0 , |
C ¹ 0 уравнение (3.2) примет |
вид |
||||||
By + C = 0 или |
y = − |
C |
. |
Это уравнение |
прямой на плоскости, |
||||
|
|||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
параллельной |
оси |
Ox |
и |
проходящей |
через точку 0;− |
|
. |
||
|
|||||||||
|
|
|
|
|
|
|
|
B |
|
(рис.3.8)
y
|
l |
0 |
|
x |
|
|
|
|
|
|
|
− C |
B |
|
|
|
|
||
|
|
|
Рис. 3.8 |
|
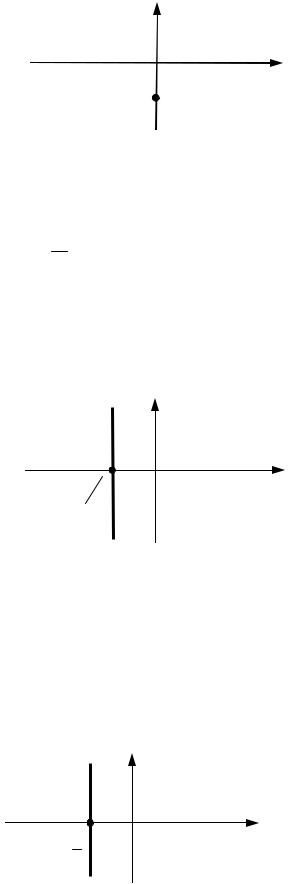
Пример. Построить прямую l : 3y + 6 = 0. |
||||
Решение. Здесь A = 0 , B = 3, |
C = 6. Уравнение прямой l |
|||
является общим уравнением прямой на плоскости, параллельной оси Ox и проходящей через точку ( 0;−2) (рис. 3.9).
30
y
|
|
0 |
x |
|
|
l |
-2 |
|
|
|
|
|
Рис. 3.9 |
|
4. При A ¹ 0 , B = 0 , |
C ¹ 0 |
уравнение (3.2) примет вид |
||
Ax + C = 0 или x = − C .
A
Это уравнение прямой на плоскости, параллельной оси Oy и
|
− |
C |
|
|
проходящей через точку |
|
; 0 (рис. 3.10). |
||
A |
||||
|
|
|
y
−C |
0 |
x |
A |
|
|
|
|
Рис. 3.10 |
Пример. Построить прямую l : 2x +1 = 0 . |
||
Решение. Здесь A = 2 , |
B = 0 , |
C = 1. Уравнение прямой l |
является общим уравнением прямой на плоскости, параллельной
|
− |
1 |
|
|
оси Oy и проходящей через точку |
|
; 0 (рис. 3.11). |
||
2 |
||||
|
|
|
y
− 1 |
0 |
x |
2
Рис. 3.11
31

5. |
При |
A = 0 , |
B ¹ 0 , |
C = 0 |
уравнение |
(3.2) |
примет |
вид |
By = 0 или y = 0. Это уравнение координатной оси Ox . |
|
|||||||
6. |
При |
A ¹ 0 , |
B = 0 , |
C = 0 |
уравнение |
(3.2) |
примет |
вид |
Ax = 0 или x = 0. Это уравнение координатной оси Oy . |
|
|||||||
Итак, рассмотрены все возможные случаи общего уравнения
(3.2) прямой на плоскости.
Уравнение прямой, проходящей
через две заданные точки
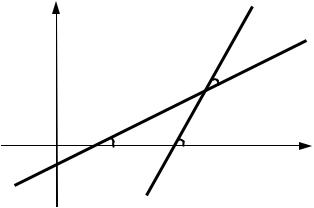
Выведем уравнение прямой l , проходящей через две
заданные точки M1 (x1; y1 ) |
и |
M 2 (x2 ; y2 ) на |
плоскости |
xOy в |
||||||||
прямоугольной декартовой системе координат (рис. 3.12). |
|
|||||||||||
|
|
|
|
|
y |
|
M 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
l |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
Рис. 3.12 |
|
|
|
|||
Поскольку точка M1 (x1 ; y1 ) лежит на прямой l то, |
||||||||||||
подставляя |
|
в |
уравнение |
(3.5) ее координаты, записываем |
||||||||
уравнение прямой l |
в виде |
|
|
|
|
|
|
|
||||
|
|
|
l : y - y1 = k × (x - x1 ), |
|
|
(3.6) |
||||||
где k – пока неизвестный коэффициент. |
|
|
|
|||||||||
Так как прямая l проходит и через точку |
M 2 (x2 ; y2 ), |
то ее |
||||||||||
координаты должны удовлетворять уравнению (3.6), то есть: |
||||||||||||
|
y |
|
- y |
= k × (x |
|
- x ), |
откуда k = |
y2 |
− y1 |
. |
|
|
|
2 |
2 |
|
|
|
|||||||
|
|
1 |
|
|
1 |
|
x2 |
− x1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Подставляя найденное значение k в уравнение уравнение прямой, проходящей через точки M1 и
l : y − y1 = x − x1 y2 − y1 x2 − x1
(3.6), получим
M 2 :
(3.7)
32
Пример. Составить уравнение прямой l , проходящей через
точки M1 (1; 2) и M 2 (−1;3). |
|
|
||||||||
|
|
Решение. |
Подставляя в уравнение (3.7) |
x1 |
= 1, y1 = 2 и |
|||||
|
x2 = −1, y2 = 3, находим искомое уравнение прямой |
l : |
||||||||
|
y - 2 |
= |
x -1 |
; |
y - 2 |
= |
x -1 |
; - 2(y - 2) = 1×(x -1); |
x + 2 y − 5 = 0 . |
|
3 - 2 |
|
1 |
|
|||||||
|
-1 -1 |
- 2 |
|
|
|
|||||
Ответ: x + 2 y − 5 = 0.
Взаимное расположение прямых на плоскости
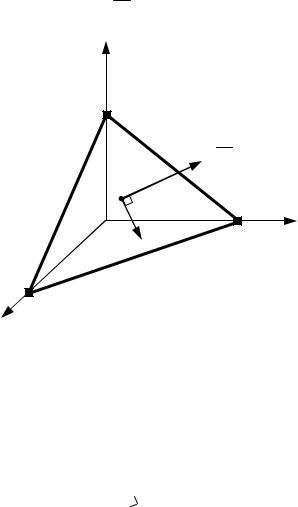
Пусть две прямые l1 и l2 заданы уравнениями с угловыми
коэффициентами k1 и k2 , |
соответственно, то есть l1 : y = k1 x + b1 ; |
l2 : y = k2 x + b2 . Требуется |
найти угол ϕ , на который надо |
повернуть прямую l , вокруг точки их пересечения до совпадения с прямой l2 . (рис. 3.13).
y
|
l2 ϕ |
l1 |
|
|
|
α1 |
α2 |
x |
0 |
|
Рис.3.13
По теореме о внешнем угле треугольника, имеем: α2 = ϕ + α1
или ϕ = α2 -α1 . Если ϕ ¹ 90O , то |
|
|
|
|
|
|
||
tgϕ = tg(α2 -α1 ) = |
|
tgα2 - tgα1 |
. |
|||||
|
|
|||||||
|
|
|
1 |
+ tgα1 ×tgα |
2 |
|
||
Но так как tgα1 = k1 и tgα2 = k2 |
, то |
|
|
|
||||
tgϕ = |
k2 - k1 |
|
|
|
|
(3.8) |
||
1 + k × k |
2 |
|
|
|
||||
1 |
|
|
|
|
|
|
||
|
|
33 |
|
|
|
|
||
Таким образом, формула (3.8) позволяет находить угол между двумя прямыми на плоскости.
Пример. Найти угол между прямыми l1 : x − 2 y + 1 = 0 и l2 : 3x + y − 3 = 0 .
Решение. Запишем общее уравнение заданных прямых l1 и l2 в виде уравнений с угловыми коэффициентами k1 и k2 ,
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
l : 2 y = x + 1 или l : y = |
1 |
x + |
1 |
, значит k = |
1 |
; |
|||||||||||||||
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
2 |
2 |
|
1 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
l2 : y = −3x + 3 , значит k2 |
= −3. |
|
|
|
|
|
|
||||||||||||||
Подставляя найденные значения k |
= |
1 |
и k |
|
= −3 в формулу |
||||||||||||||||
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3.8), находим угол ϕ между прямыми l1 |
и l2 : |
|
|
|
|||||||||||||||||
|
- 3 - |
1 |
|
- |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
tgϕ = |
|
2 |
|
= |
2 |
|
= 7 , откуда ϕ = arctg 7 . |
||||||||||||||
|
|
|
|
||||||||||||||||||
|
1 + |
1 |
× (- 3) |
- |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: ϕ = arctg 7 .
Заметим, что если требуется вычислить острый угол между прямыми, то правая часть формулы (3.8) берется по модулю, то
есть
|
tgϕ = |
|
k2 - k1 |
|
|
. |
|
|
|
1 + k × k |
2 |
|
|||
|
|
|
|
1 |
|
|
|
Если прямые l1 : y = k1 x + b1 ; |
l2 : y = k2 x + b2 параллельны, то |
||||||
ϕ = 0 и tgϕ = 0 , следовательно, |
из формулы (3.8) получаем, что |
||||||
k2 − k1 |
= 0, то есть k2 = k1 . И обратно, если прямые l1 и l2 таковы, |
||||||
что k1 |
= k2 , значит tgϕ = 0 , то есть прямые параллельны. |
||||||
|
34 |
|
|
|
|||

Если |
прямые |
l и |
l |
2 |
перпендикулярны (ϕ = π ), то |
|||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
ctgϕ = |
1 + k1 × k2 |
= 0 , |
откуда |
k × k |
|
= -1. Справедливо и обратное |
||
|
2 |
|||||||
|
k2 |
− k1 |
|
1 |
|
|||
|
|
|
|
|
|
|||
утверждение.
Пример. Составить уравнение прямой l , проходящей через точку M (1; 2) и перпендикулярной прямой L : 3x + 2 y − 5 = 0 .
Решение. Перепишем общее уравнение прямой L в виде
уравнения прямой с угловым коэффициентом kL :
L : 3x + 2 y − 5 = 0 ,
L : 2 y = −3x + 5 ,
L : y = − 3 x + 5 , значит k |
|
= − |
3 |
. |
|
|
|
|
|
|
|||||
L |
|
|
|
|
|
|
|
||||||||
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
Прямые l и L перпендикулярны по условию, значит |
|||||||||||||||
kl × kL = -1, следовательно, kl = − |
1 |
= |
2 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
kL |
|
3 |
|
|
|
|
|
|
|||
Подставляя в уравнение (3.5) k |
|
= |
|
2 |
, x = 1, |
y |
|
= 2 находим |
|||||||
l |
|
|
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
искомое уравнение прямой l :
l : y − 2 = 2 (x −1) 3
l : 3y − 6 = 2x − 2 l : 2x − 3y + 4 = 0
Ответ: 2x − 3y + 4 = 0.
35
§ 4. Плоскость
Переходим далее к аналитической геометрии в пространстве. Объектом изучения теперь будет плоскость. Если в трехмерном пространстве задана прямоугольная декартова система координат, то положение любой точки однозначно определяется тремя числами - её координатами. Найдем уравнение, связывающее координаты любой точки,
принадлежащей плоскости. Способ получения уравнения плоскости аналогичен выводу общего уравнения прямой на плоскости.
|
Общее уравнение плоскости |
|
|||
Пусть в |
прямоугольной |
декартовой системе |
координат |
||
|
M 0 ( x0 ; y0; z0 ) и |
вектор |
|
{A; B;C} . |
|
задана точка |
N |
Требуется |
|||
составить уравнение плоскости, |
проходящей через точку M 0 и |
||||
перпендикулярной вектору N (рис. 4.1).
z
N = (A; B;C )
M 0
0 |
M |
y |
|
||
|
|
x
Рис. 4.1
36
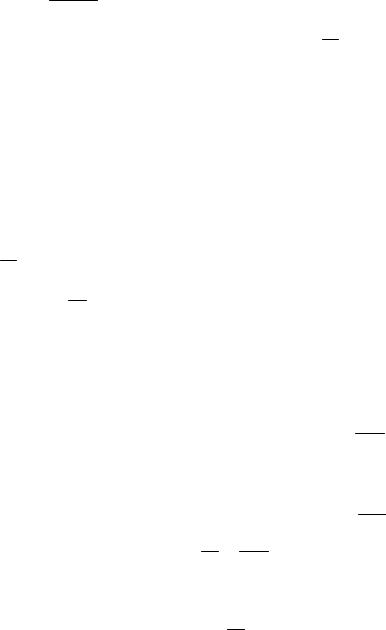
Выберем произвольную точку M ( x; y; z) на плоскости.
Тогда вектор M 0M = {x - x0; y - y0 ; z - z0} лежит на плоскости. Так
как плоскость перпендикулярна вектору |
N по условию, то и |
||||||||
|
|
|
|
|
|
|
|
, а значит скалярное |
|
вектор M 0 M перпендикулярен вектору |
N |
||||||||
произведение |
|
× |
|
= 0 , или в координатах |
|
||||
M 0 M |
N |
|
|||||||
|
A ×(x - x0 ) + B ×( y - y0 ) + C ×(z - z0 ) = 0 . |
(4.1) |
|||||||
Уравнение (4.1) является уравнением |
плоскости, |
||||||||
проходящей через точку M 0 (x0 ; y0; z0 ) и перпендикулярной вектору N {A; B;C} .
Вектор N { A; B;C} называется вектором нормали плоскости.
Пример. Составить уравнение плоскости, проходящей через точку M 0 (1;2;3) и перпендикулярной вектору PQ , если P( 0;1;7)
и Q(-1;2;5).
Решение. Находим координаты вектора PQ , являющегося вектором нормали плоскости: N = PQ = {−1;1;−2} .
Подставляя в уравнение (4.1) координаты точки M 0 (1;2;3) и
найденные координаты вектора N , находим искомое уравнение плоскости:
-1×( x -1) +1×( y - 2) - 2 ×( z - 3) = 0 или
−x + y − 2z + 5 = 0
Ответ: −x + y − 2z + 5 = 0 .
Далее преобразуем уравнение (4.1):
Ax − Ax0 + By − By0 + Cz − Cz0 = 0 или
Ax + By + Cz + (− Ax0 − By0 − Cz0 ) = 0 .
37
Обозначив D = −Ax0 − By0 − Cz0 , получаем общее уравнение
плоскости вида |
|
Ax + By + Cz + D = 0. |
(4.2) |
Исследуем уравнение (4.2)
1. При A ¹ 0 , B ¹ 0 , C ¹ 0 , D ¹ 0 уравнение (4.2) примет
вид
Ax + By + Cz = −D .
Разделив обе части последнего уравнения на (−D)
|
|
|
x |
+ |
|
y |
|
+ |
y |
|
= 1, |
||||||
|
|
− D |
− D |
|
− D |
|
|||||||||||
|
|
|
|
A |
|
|
|
|
B |
|
C |
|
|||||
и обозначив |
a = − D |
, b = − D |
B |
, c = − D |
C |
, получаем уравнение |
|||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||
плоскости «в отрезках»: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
+ |
y |
+ |
z |
= 1, |
|
|
(4.3) |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a |
|
b |
c |
|
|
|
|
|
|
||||
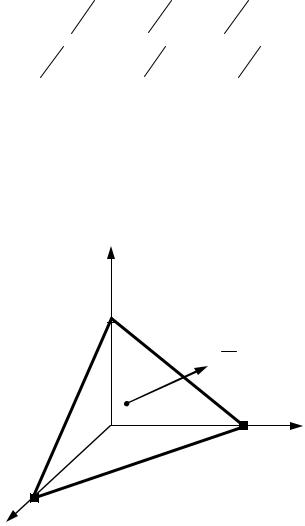
где a , b и c - величины отрезков, которые плоскость отсекает от осей координат (рис. 4.2).
z
 − CD
− CD
N = (A; B;C )
|
− D |
|
0 |
B |
|
y |
||
|
− D |
A |
x |
Рис. 4.2
38
Пример. Составить уравнение плоскости, проходящей через точку M 0 ( 1;2;3) и отсекающей от осей координат равные
отрезки.
Решение. Используем уравнение (4.3). Так как a = b = c по условию, то его можно переписать в виде x + y + z = a .
Поскольку точка M 0 ( 1;2;3) лежит на плоскости, то,
подставляя ее координаты в последнее уравнение, находим a = 6 .
Следовательно, |
x + y + z = 6 – уравнение искомой плоскости. |
|||||||||||||||
Ответ: x + y + z = 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Построить плоскость |
6x − 2y + 3z −12 = 0 . |
|||||||||||||||
Решение. Приведем заданное уравнение к уравнению вида |
||||||||||||||||
(4.3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
− |
2 y |
+ |
3z |
=1; |
|
x |
|
+ |
|
y |
+ |
z |
=1. |
|
|
|
|
|
2 |
|
|
|
|||||||||
|
12 12 |
|
12 |
|
|
|
|
−6 |
4 |
|
||||||
Отметим на оси Ox точку x = 2 , |
на оси Oy точку y = −6, на |
|||||||||||||||
оси Oz точку |
z = 4 , и |
|
через |
эти |
точки |
|
проведем искомую |
|||||||||
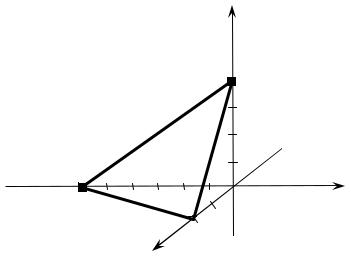
плоскость (рис. 4.3).
z
4
− 6 |
0 |
y |

 2
2
x
Рис. 4.3
39
