
9771
.pdf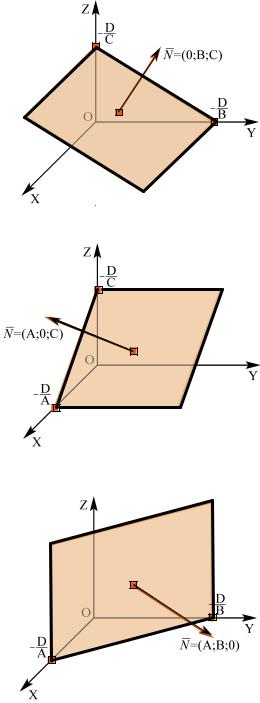
2. Рассмотрим случай, когда в уравнении (4.2) коэффициент
A = 0 . |
|
|
|
|
|
|
|
|
|
|
uur |
|
|
||
Тогда |
вектор |
нормали |
N = 0; B;C оказывается |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
} |
перпендикулярен |
оси |
Ox , |
а плоскость By + Cz + D = 0 , тем |
||||||||||||
самым, - |
параллельна |
|
этой оси. Аналогично – |
при нулевых |
|||||||||||
коэффициентах B или |
C (рис.4.4). |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.4
40
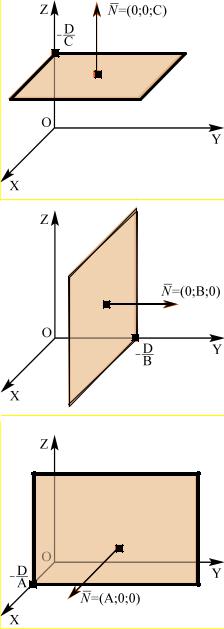
3. Если равны нулю два |
коэффициента перед переменными |
уравнения (4.2), например, |
A = B = 0 , то вектор нормали |
uuur
N = {0;0;C}перпендикулярен координатной плоскости xOy , а
сама плоскость Cz + D = 0 – параллельна ей. Аналогично – при двух других нулевых коэффициентах перед переменными (рис. 4.5).
Рис. 4.5
41

4. Если в уравнении (4.2) D = 0 , то оно задаёт плоскость,
проходящую через начало координат. Для её построения достаточно рассмотреть прямые, которые получаются при пересечении плоскости с координатными плоскостями (рис. 4.6).
Рис. 4.6
5. Допустим, что нулевыми оказываются коэффициент при
одной из |
переменных и свободный коэффициент. Например, |
A = D = 0. |
В этом случае уравнение (4.2) приобретает вид |
By + Cz = 0 и задаёт плоскость, проходящую через ось Ox . Для её построения достаточно добавить ещё одну прямую – например, линию пересечения плоскости с координатной плоскостью yOz (рис. 4.7). При B = D = 0 или C = D = 0
ситуации аналогичны (рис. 4.8).
Рис. 4.7
42
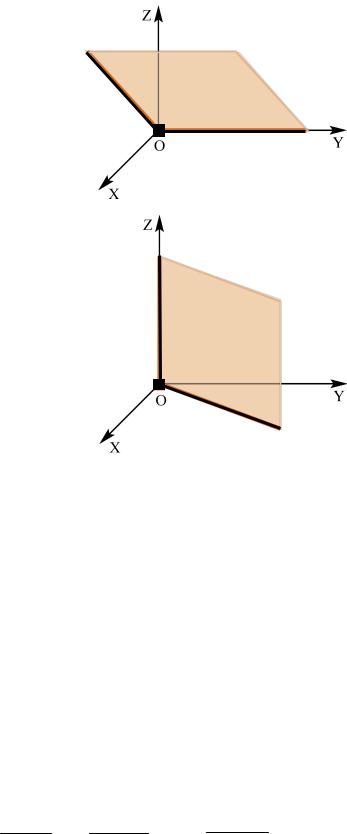
Рис. 4.8
Итак, мы рассмотрели все возможные случаи общего
уравнения (4.2) плоскости.
Уравнение плоскости,
проходящей через три заданные точки
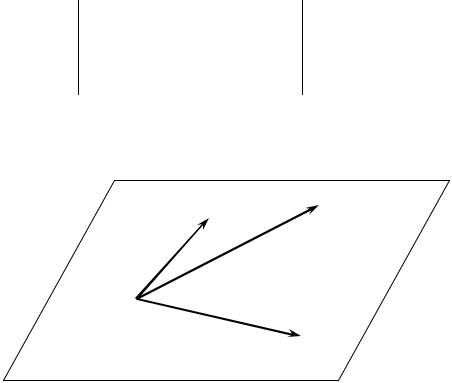
Выведем теперь уравнение плоскости, проходящей через три заданные точки M1 ( x1; y1; z1 ) , M2 (x2; y2; z2 ) и M3 (x3; y3; z3 )
в прямоугольной декартовой системе координат. Для этого рассмотрим произвольную точку плоскости M ( x; y; z) . Три
вектора M1M , M1M 2 и M1M3 компланарны (рис. 4.9),
поэтому их смешанное произведение равно нулю.
43
|
Подставляя |
в формулу |
(2.4) |
координаты |
векторов |
|||||
|
|
м |
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
||
M M = нпx- x ; y- y ; z- z , |
M M = нпx - x ; y - y ; z - z |
|||||||||
|
|
|
|
|
1} |
|
|
п |
|
1 2 1} |
1 |
|
п |
1 |
1 |
1 2 |
|
п 2 |
1 2 |
||
|
|
оп |
|
|
|
|
|
оп |
|
|
|
|
м |
|
x ; y - |
y ; z - |
z , получаем |
|
M M |
|
||||
и |
= нпx - |
|||||
|
1 3 |
п |
3 |
1 3 |
1 3 |
1} |
|
|
оп |
|
|
|
|
x − x1 x2 − x1 x3 − x1
y − y1 y2 − y1 y3 − y1
z − z1
z2 − z1 = 0. (4.4)
z3 − z1
Раскрывая этот определитель, получим общее уравнение плоскости вида (4.2).
M2
M
M1
M3
Рис. 4.9
Пример. Составить уравнение плоскости, проходящей через точки M1 (1;2;3) , M 2 (−1;4;3) и M3 (2;2;4) .
Решение. Подставляем в уравнение (4.4) координаты
заданных точек:
|
x -1 |
y - 2 z -3 |
|
= |
|
или |
|
x −1 y − 2 z − 3 |
|
= |
|
|||
|
|
|
|
|
|
|||||||||
|
-1-1 |
4 - 2 |
3-3 |
|
0 |
|
− |
2 |
0 |
|
0. |
|||
|
|
|
|
|
2 |
|
|
|||||||
|
2 -1 |
2 - 2 |
4 -3 |
|
|
|
|
|
1 |
0 |
1 |
|
|
|
Раскрывая |
определитель, |
приходим |
к |
уравнению |
||||||||||
2×(x -1) + 2×( y - 2) − 2×(z -3) = 0 или |
|
x + y − z = 0. |
|
|
|
|
||||||||
Ответ: x + y − z = 0.
44
§ 5. Линии второго порядка
До сих пор в аналитической геометрии мы изучали прямые и плоскости, в уравнения которых переменные x , y и z входят в первой степени. Сейчас переходим к рассмотрению кривых на плоскости, задаваемых более сложными алгебраическими уравнениями, включающими вторые степени текущих координат x и y или их взаимное произведение.
Уравнение вида
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 |
(5.1) |
называется общим уравнением линии (кривой) второго
порядка. В нём коэффициенты A, |
B , |
C , D , E и F — любые |
действительные числа, для которых |
A2 + B2 + C 2 ¹ 0 , т.е. по |
|
крайней мере, одно из чисел A , |
B или C отлично от нуля. |
|
Например, уравнение x2 + xy + y2 - |
y - |
5 = 0 относится к классу |
уравнений второго порядка и получается из общего вида (5.1) при конкретном значении коэффициентов.
Простейшим примером кривой, задаваемой уравнением (5.1),
является окружность. Окружность определяется как множество точек плоскости, равноудалённых от заданной точки (центра).
Вводим на плоскости прямоугольную декартову систему координат, совместив её начало с центром окружности.
Координаты произвольной точки M , лежащей на окружности,
обозначим x и y . Эти координаты связаны между собой равенством x2 + y2 = R2 , которое и представляет собой уравнение окружности. Ему удовлетворяют координаты каждой точки окружности и не удовлетворяют координаты любой другой точки плоскости, не лежащей на ней. Видим, что это уравнение является уравнением второго порядка.
45
К другим линиям, задаваемым уравнением (5.1), относятся эллипс, гипербола и парабола. В некоторых случаях получаются пара пересекающихся или параллельных прямых, одна прямая или точка. Изучение этих классических линий мы, как и для окружности, будем начинать с их определения. Дальше будем ставить задачу вывести уравнение, которому удовлетворяют координаты точек в том и только том случае, когда точки лежат на рассматриваемой линии. Для получения уравнения будем вводить систему координат, располагая её по отношению к линии так, чтобы уравнение в этой системе имело простейший вид,
называемый каноническим уравнением линии.
Эллипс
Эллипсом называется множество всех точек M плоскости,
сумма расстояний каждой из которых до двух данных точек F1 и
F2 есть величина постоянная (её принято обозначать 2a ). В этих обозначениях можно коротко записать определение эллипса в виде равенства MF1 + MF2 = 2a . Точки F1 и F2 называются
фокусами эллипса. Расстояние F1F2 между фокусами обозначают 2c .
Из определения непосредственно вытекает способ построения: если концы нерастяжимой нити длины 2a закрепить в точках F1 и F2 , затем натянуть нить остриём карандаша, то при движении острия оно будет вычерчивать выпуклую замкнутую линию (овал).
Сумма расстояний от произвольной точки M до двух фиксированных точек F1 и F2 не может быть меньше расстояния между точками F1 и F2 : MF1 + MF2 ³ F1F2 . Будем предполагать,
что это неравенство строгое, т.е. 2a > 2c или a > c .
46
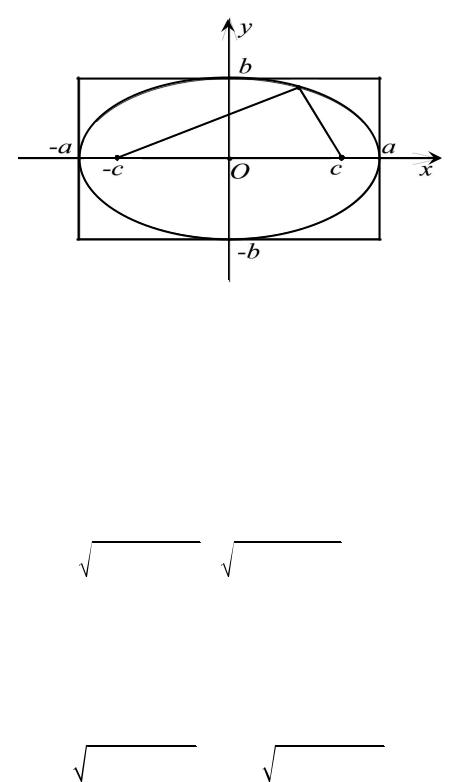
Выведем теперь уравнение эллипса. Для этого введём прямоугольную декартову систему координат. В качестве оси абсцисс мы возьмём прямую, проходящую через F1 и F2 , считая её направленной от F1 к F2 , начало системы координат поместим в середине отрезка F1F2 (рис. 5.1).
|
M |
F1 |
F2 |
Рис. 5.1
В этой системе координат для произвольной точки M
координаты обозначим через x и y . Фокусы, оказавшись теперь
на оси Ox симметрично относительно начала, будут иметь координаты F1 (−c;0) и F2 (c;0) . Расстояния F1M и F2 M между
точками заменим их выражениями через координаты. Получим
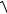
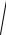 ( x + c)2 + y2 +
( x + c)2 + y2 + 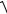
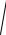 ( x − c)2 + y2 = 2a .
( x − c)2 + y2 = 2a .
По существу, это соотношение представляет собой уравнение эллипса. Ему удовлетворяют координаты точек в том и только том случае, когда точки лежат на эллипсе. Проведём алгебраические преобразования, упрощающие эту запись. Для этого сначала уединим в уравнении первый радикал
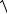
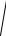 ( x + c)2 + y2 = 2a −
( x + c)2 + y2 = 2a − 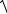
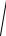 ( x − c)2 + y2 .
( x − c)2 + y2 .
47
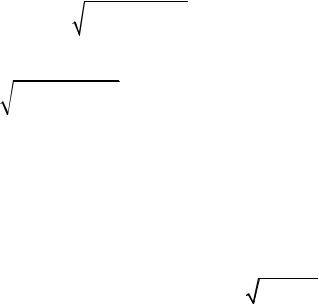
Возведём в квадрат обе части полученного равенства
( x + c)2 + y2 = 4a2 − 4a
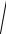 ( x − c)2 + y2 + ( x − c)2 + y2 ,
( x − c)2 + y2 + ( x − c)2 + y2 ,
раскроем скобки и после сокращения получим
a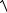
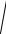 ( x − c)2 + y2 = a2 − cx .
( x − c)2 + y2 = a2 − cx .
Возведя в квадрат обе части последнего равенства, найдём
a2 x2 − 2a2cx + a2c2 + a2 y2 = a4 − 2a2cx + c2 x2 , |
|
||||||||
откуда |
(a2 − c2 ) x2 + a2 y2 = a2 (a2 − c2 ) . |
|
|||||||
Мы отмечали, |
что |
a > c , значит |
a2 − c2 |
> 0 , и |
можно |
||||
|
|
|
|
b = |
|
, |
|
||
ввести в рассмотрение новую величину |
a2 − c2 |
чтобы |
|||||||
придать уравнению вид |
|
|
|
|
|
|
|
||
|
b2 x2 + a2 y2 = a2b2 . |
|
|
|
|
||||
При этом получается b < a . Разделив обе части на |
a2b2 , получим |
||||||||
|
2 |
2 |
|
|
|
|
|
||
|
|
x |
+ |
y |
= 1. |
|
|
|
(5.2) |
|
|
2 |
2 |
|
|
|
|||
|
|
a |
|
b |
|
|
|
|
|
Это уравнение называется каноническим уравнением эллипса. Особенностью уравнения является то, что оно содержит
x и y только в чётных степенях, |
поэтому если точка ( x, y ) |
|||||
принадлежит |
эллипсу, то |
ему принадлежат и |
точки |
( x;− y ), |
||
(−x; y), (−x, − y ). Отсюда |
следует, |
что |
эллипс |
симметричен |
||
относительно |
осей Ox |
и Oy , также |
относительно |
начала |
||
координат. Оси симметрии эллипса называются его осями, а
точка пересечения осей – центром эллипса. Точки, в которых эллипс пересекает свои оси, называются его вершинами.
Положив y = 0 в уравнении (5.2), найдём две вершины A1 (−a;0)
и A2 (a;0) на оси Ox . Положив x = 0 , найдём две точки пересечения эллипса с осью Oy : B1 (0;−b) и B2 (0;b) (рис. 5.1).
48

Итак, эллипс имеет четыре вершины A1, A2 , B1, B2 , которые ограничивают на осях отрезки A1 A2 = 2a и B1B2 = 2b (эти отрезки тоже принято называть осями эллипса), отрезки ОA1 = a
и ОB1 = b называются соответственно большой и малой полуосями эллипса.
Исследовав форму эллипса путём анализа его канонического
уравнения, можно теперь непосредственно построить в первой
|
y = |
b |
|
|
|
|
четверти график функции |
|
a2 − x2 |
и, отразив его |
|||
a |
||||||
|
|
|
|
|
симметрично относительно осей координат, получить овальную замкнутую кривую, изображённую на рисунке 5.1. Отметим, что при этом все точки эллипса лежат внутри прямоугольника,
образованного прямыми x = a , x = −a , y = b , y = −b .
Введём ещё одну величину, характеризующую форму
эллипса. Отношение ε расстояния между фокусами эллипса к
длине его большой оси называется эксцентриситетом эллипса:
ε = |
c |
|
|
|
|
|
|
|
|
|
|
|
< ε < 1, |
|
a > c > 0 . |
||||
a . Величина эксцентриситета 0 |
так как |
||||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
2 |
|
c2 |
a2 − b2 |
b |
2 |
|
b 2 |
|
|||||||
Поскольку |
ε |
|
= |
|
|
= |
|
|
= 1 − |
|
, то |
ε = |
1 − |
|
, |
||||
|
a |
2 |
a |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|||||||
b = 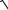
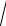 1 − ε 2 . a
1 − ε 2 . a
Видим, что эксцентриситет определяется соотношением осей
эллипса. В |
случае |
ε = 0 (если |
a = b ) эллипс |
превращается в |
||
окружность |
с |
уравнением |
x2 + y2 = a2 . |
Чем |
ближе |
|
эксцентриситет к |
единице, тем |
меньше отношение |
b |
и тем |
||
|
||||||
a |
||||||
больше эллипс вытянут.
49
