
9745
.pdfТакже как и для кривых второго порядка, для поверхностей второго порядка существует полная классификация. С помощью подходящего параллельного переноса и поворота осей координат
(теперь уже выполняемых в пространстве) любое уравнение второго порядка может быть приведено к одному из семнадцати видов. Этим уравнениям в пространстве отвечают классические поверхности: эллипсоид, однополостный и двуполостный гиперболоиды, конус, эллиптический и гиперболический параболоиды, а также целая группа поверхностей, называемых цилиндрическими.
Цилиндрические поверхности
Поверхность, состоящая из параллельных прямых (так
называемых образующих), проходящих через каждую точку
заданной линии L (направляющей), называется
цилиндрической поверхностью. Образно можно представить,
что цилиндрические поверхности образуются движением прямой,
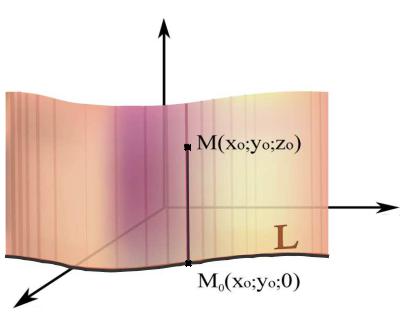
которая перемещается в пространстве вдоль кривой L , сохраняя постоянное направление (рис. 7.1).
В качестве направляющей цилиндрической поверхности рассмотрим расположенную в плоскости xOy линию L , которая
задаётся уравнением |
F(x, y) = 0. Пусть M0 (x0 , y0 , 0) – |
произвольная точка |
направляющей (рис. 7.1). Тогда |
F (x0 , y0 ) = 0 . |
|
Рассмотрим цилиндрическую поверхность, образующие которой параллельны координатной оси Oz . Если такая
образующая проходит через M0 (x0 , y0 , 0) , |
то абсциссы всех её |
|
точек равны x0 , а ординаты равны |
y0 . Поэтому координаты |
|
произвольной точки M (x0 , y0 , z0 ) этой |
образующей тоже |
|
удовлетворяют уравнению F (x, y) = 0 |
при любом значении z0 . |
|
z
y
x
Рис. 7.1
Точка M0 (x0 , y0 ,0) выбиралась произвольно, поэтому можно
утверждать, что координаты всех точек цилиндрической поверхности удовлетворяют уравнению F (x, y) = 0 .
Ясно, |
что |
уравнение |
вида |
F (x, z) = 0 |
задаёт |
цилиндрическую поверхность с |
образующими, параллельными |
||||
оси Oy , |
а уравнение вида F ( y, z) = 0 |
задаёт цилиндрическую |
|||
поверхность с образующими, параллельными оси O x .
Если направляющей цилиндрической поверхности является кривая второго порядка, то поверхность называется цилиндрической поверхностью второго порядка (или цилиндром второго порядка). В зависимости от конкретного вида уравнения получаются различные типы цилиндров второго порядка. Их
названия соответствуют названиям направляющих линий L .
Например, уравнение |
x2 |
+ |
y2 |
= 1 |
задаёт в пространстве |
|
a2 |
b2 |
|||||
|
|
|
|
цилиндрическую поверхность с образующими, параллельными оси Oz . Его направляющей является эллипс, а поверхность,
задаваемая этим уравнением, называется эллиптическим
61
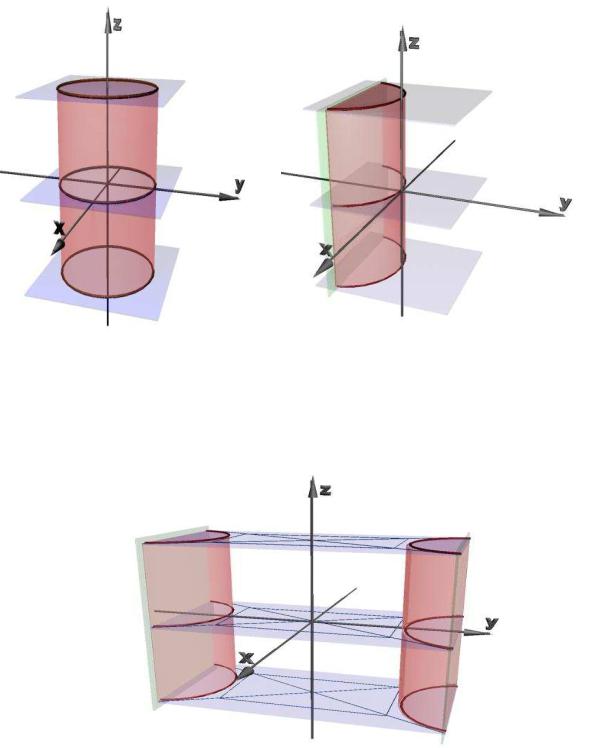
цилиндром (рис. 7.2). Частным случаем эллиптического цилиндра является круговой цилиндр. Его уравнение в каноническом виде имеет вид x2 + y2 = R2 .
Уравнение вида x2 = −2 py определяет в пространстве
параболический цилиндр (рис. 7.2).
|
|
|
|
Рис. 7.2 |
|
Уравнение вида |
y2 |
− |
x2 |
= 1 определяет в пространстве |
|
b2 |
a2 |
||||
|
|
|
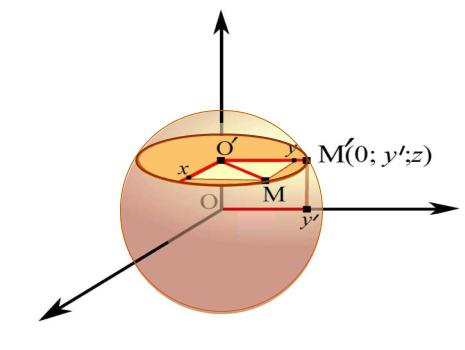
гиперболический цилиндр (рис. 7.3).
Рис. 7.3
62
Поверхности вращения
Поверхности вращения образуются вращением какой-либо плоской линии L (образующей) вокруг прямой (оси поверхности вращения), расположенной в плоскости этой линии. Примером служит сфера: её можно рассмотреть как поверхность, образованную вращением полуокружности вокруг её диаметра. Покажем, как можно получить уравнение поверхности вращения, исходя из уравнения образующей
(лежащей в одной из координатных плоскостей) и уравнения оси вращения (совпадающей с одной из координатных осей,
расположенных в той же плоскости).
Будем вращать расположенный в плоскости yOz эллипс с
уравнением |
y2 |
+ |
z2 |
=1 |
вокруг |
координатной оси Oz . |
|
b2 |
c2 |
||||||
|
|
|
|
|
Полученную поверхность рассечём плоскостью, параллельной
координатной плоскости xOy и проходящей через фиксированную точку O′(0, 0, z) (рис. 7.4).
z
y
x
Рис. 7.4
63
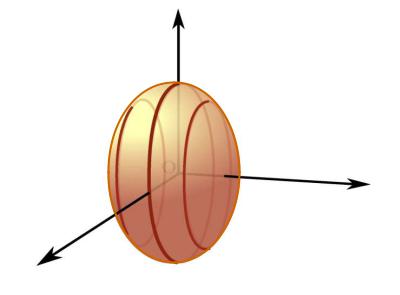
Пусть M (x, y, z) – |
произвольная точка поверхности вращения, |
||||
лежащая в плоскости сечения. Рассмотрим в |
плоскости yOz |
||||
точку поверхности |
M ′(0, y′, z) . Её |
ордината |
по абсолютной |
||
величине равна |
радиусу окружности, на которой лежит точка |
||||
M (x, y, z) , |
т.е. O′M ′ = O′M , поэтому x2 + y2 = y′2 . Находящаяся в |
||||
плоскости |
yOz |
точка M ′(0, y′, z) |
принадлежит и плоскости |
||
сечения, и исходному эллипсу. Это означает, что её координаты
удовлетворяют уравнению |
y′2 |
+ |
z2 |
=1. |
Подставляя в это |
|||||||||||||||||||
b2 |
c2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
уравнение |
выражение |
y′ |
|
через |
x |
и |
y , |
получим |
||||||||||||||||
2 |
2 |
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
+ |
|
y |
+ |
|
|
|
= 1. Это и есть |
|
искомое уравнение |
поверхности |
||||||||||||
|
2 |
2 |
c |
2 |
||||||||||||||||||||
|
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вращения, называемой эллипсоидом вращения. |
|
|
||||||||||||||||||||||
|
|
|
Если вращать эллипс |
y2 |
+ |
z2 |
|
=1 |
вокруг оси Oy , получится |
|||||||||||||||
|
|
|
c2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
||||
другой |
|
эллипсоид вращения |
(рис. |
7.5) |
с |
уравнением |
||||||||||||||||||
2 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
+ |
y |
|
+ |
z |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
c |
|
|
|
b |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
||||
z
y
x
Рис. 7.5
64
От этих примеров нетрудно перейти к алгоритму получения уравнения поверхности вращения по уравнению исходной кривой, если осью вращения служит одна из координатных осей.
В уравнении кривой слагаемое с переменной, наименование которой совпадает с наименованием оси вращения, останется без изменения, а квадрат другой переменной меняется на сумму квадратов этой переменной и переменной, отсутствовавшей в уравнении.
§8. Канонические уравнения поверхностей
второго порядка
Теперь перейдем к другим поверхностям второго порядка,
определяемым общим уравнением
Ax2 + By2 + Cz2 + 2Dxy + 2Exz +
+2Fyz + 2Gx + 2Hy + 2Kz + L = 0 .
Каждая поверхность может быть построена по её уравнению методом сечений. Проследим, как образуются поверхности второго порядка, проявляясь постепенно по мере стыковки разных сечений.
Эллипсоиды
Начнём с уравнения эллипсоида
x2 |
+ |
y2 |
+ |
z2 |
= 1 . |
(8.1) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Уравнение сечения этой поверхности координатной плоскостью xOz получается, если в исходном уравнении (8.1) принять y = 0 :
x2 |
+ |
z2 |
= 1. По виду уравнения мы узнаём эллипс и можем |
|
a2 |
c2 |
|||
|
|
изобразить его в соответствующей плоскости (рис. 8.1).
65
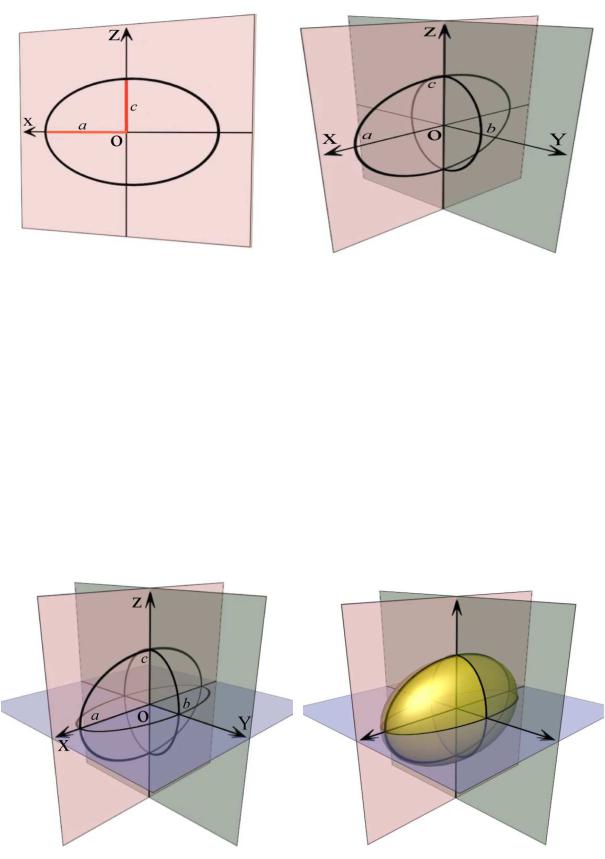
Рис. 8.1
При x = 0 из (8.1) получаем уравнение другого эллипса,
располагающегося в плоскости yOz и имеющего те же точки
пересечения с осью Oz , что и первый эллипс: |
y 2 |
+ |
z 2 |
= 1 . |
|
b2 |
c2 |
||||
|
|
|
Рисунок дополняется эллипсом в плоскости xOy (рис. 8.2).
Рис. 8.2
66

Рассмотрим произвольную плоскость z = h (где h – любое
число), параллельную xOy . Сечение исходной поверхности (8.1)
этой плоскостью задаётся уравнением
x |
2 |
|
y |
2 |
|
h |
2 |
|
|
|
x |
2 |
|
|
|
+ |
|
|
y |
2 |
|
|
|
= 1 |
|
|
+ |
= 1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||||||
a2 |
b2 |
c2 или |
|
2 |
(1 − |
h |
2 |
|
− |
h |
||||||||||||||||
|
|
a |
|
) b |
(1 |
|
) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c2 |
|
c2 |
|
|
||||||||||||
То есть при всех h < c в сечении эллипсоида (8.1) плоскостями
z = h |
получаются |
|
эллипсы |
с полуосями |
a |
= a 1− |
h2 |
|
|
и |
|||||||||
c2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
b = b 1− |
h2 |
|
. Если |
|
h |
|
< c , то a |
< a , b < b . При уменьшении |
|
h |
|
|
|||||||
|
|
|
|
|
|||||||||||||||
|
|||||||||||||||||||
h |
|
c2 |
|
|
|
|
|
|
h |
h |
|
|
|
|
|
|
|
|
|
|
|
|
и bh |
|
|
|
|
|
|
|
|
|
|
|
|
||||
полуоси ah |
|
увеличиваются, достигая наибольших значений |
|||||||||||||||||
ah = a |
и bh = b , |
если |
|
h = 0 . Таким образом, |
«самый крупный» |
||||||||||||||
эллипс |
образуется в |
|
сечении координатной |
плоскостью |
xOy . |
||||||||||||||
Аналогичная картина получается в сечениях поверхности (8.1)
плоскостями, параллельными координатным плоскостям xOz и
yOz .
Отметим, что на плоскости нет точек, отвечающих условию z > c . Т.е. у поверхности, которую мы строим, нет пересечения с
плоскостями z = h |
при |
|
|
h |
> c , как и с плоскостями |
x = h при |
|||||||||||
|
h |
|
> a |
или |
y = h при |
|
h |
|
> b Сечение поверхности плоскостями |
||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
z = c |
|
z = −c |
|
|
|
|
|
|
||||||||
|
или |
даёт |
точку, так как в уравнении |
при этом |
|||||||||||||
получается |
|
x2 |
+ |
y2 |
= 0 . |
|
|
Общий вид поверхности |
отражаем |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|||||
рисунком 8.2. Вполне естественно, что эта поверхность носит название «эллипсоид» – по названиям сечений.
Эллипсоид обладает тремя взаимно перпендикулярными плоскостями симметрии (при данном выборе осей они совпадают
67
с координатными плоскостями). Величины a , b и c называются полуосями эллипсоида. Если две из трёх полуосей одинаковы, то,
эллипсоид становится эллипсоидом вращения. Если a = b = c , то уравнение (8.1) определяет сферу.
Гиперболоиды
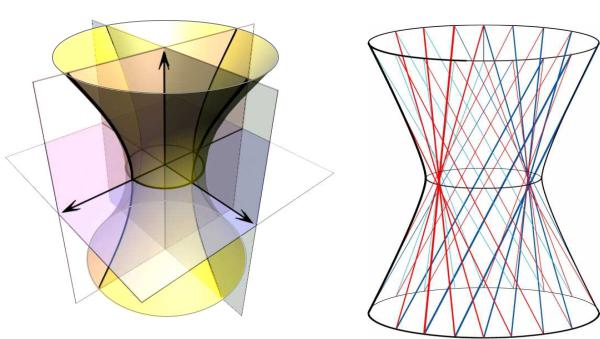
Рассмотрим уравнение однополостного гиперболоида
x2 |
+ |
y2 |
− |
z2 |
= 1. |
(8.2) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
Всечениях координатными плоскостями xOz и yOz
поверхности, определяемой этим уравнением, получаются гиперболы, а в сечениях, параллельных координатной плоскости xOу – эллипсы. В целом поверхность выглядит, как бесконечная трубка, расширяющаяся в обе стороны от горлового эллипса (рис. 8.3).
Рис. 8.3
68

Однополостный гиперболоид обладает тремя плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями). Величины a , b и c называются полуосями однополостного гиперболоида. Если a = b, то
однополостный гиперболоид становится поверхностью вращения
и может быть получен вращением |
гиперболы |
|
y2 |
− |
z2 |
=1 |
|
|
b2 |
c2 |
|||||
|
|
|
|
|
|
||
вокруг оси Oz , которую она не пересекает. |
|
|
|
|
|
||
Однополостный |
гиперболоид |
обладает |
интересным |
||||
геометрическим свойством, которое можно обнаружить, если представить уравнение (8.2) в виде
x2 |
− |
z2 |
= 1− |
y2 |
|
a2 |
c2 |
b2 |
|||
|
|
или, эквивалентно,
x |
|
z x |
|
z |
|
|
y |
|
|||||
|
|
+ |
|
|
|
− |
|
|
= 1 |
+ |
|
1 |
− |
|
|
|
|
|
|||||||||
a |
|
c a |
|
c |
|
|
b |
|
|||||
y
. (8.3)
b
Наряду с этим уравнением рассмотрим систему линейных уравнений
|
x |
|
|
z |
|
|
||||
α |
|
|
+ |
|
|
|
= β 1 |
+ |
||
|
|
|
||||||||
|
a |
|
|
c |
|
|
||||
|
x |
|
|
z |
|
|
||||
|
|
|
|
|||||||
β |
|
|
− |
|
|
|
= α 1 |
− |
||
|
|
|
|
|||||||
|
a |
|
|
c |
|
|
||||
|
|
|
|
|||||||
,
b
y |
(8.4) |
|
|
||
|
. |
|
|
|
|
b |
|
|
В ней α и β - некоторые числа, не равные одновременно нулю. При фиксированных значениях α и β уравнения (8.4)
задают в пространстве конкретную прямую как пересечение плоскостей. Меняя α и β , мы получаем бесконечную систему прямых. Каждая из этих прямых лежит целиком на однополостном гиперболоиде.
69
