
9723
.pdf
[Введите текст]
Пример. Найти экстремумы функции f (x, y) = x2 + y2 при условии,
что её аргументы связаны соотношением 5x2 − 6xy + 5 y2 − 32 = 0 . Образуем функцию Лагранжа
F (x, y,λ) = x2 + y2 + λ( 5x2 − 6xy + 5y2 − 32) .
Приравнивая к нулю её частные производные, получаем следующую систему для нахождения координат стационарных точек
|
x + λ(5x − 3y) = 0 |
|
|||||||||
|
y + λ(−3x + 5 y) = 0 |
|
|||||||||
|
|
||||||||||
|
5x |
2 |
− 6xy + |
5 y |
2 |
− 32 |
= 0 |
||||
|
|
|
|
||||||||
Исключаем из первых двух уравнений параметр |
λ , разделив одно из них |
||||||||||
на другое |
|
|
−3 + 5k |
|
|
|
|
|
|
|
|
|
k = |
, |
k = |
y0 |
. |
||||||
|
|
|
|
||||||||
|
|
|
|
5 − 3k |
|
|
|
x0 |
|
||
Откуда k = ±1 или y0 = ± x0 . Третье уравнение системы даёт возмож- |
|||||||||||
ность найти конкретные значения координат стационарных точек. В случае
|
= x0 находим точки ( 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
2; 2 2; − 0,5 ), ( − 2 |
2; − 2 |
2; − 0,5 ) . А если |
||||||||||||
|
= −x0 , то получаем точки |
( |
|
− |
|
|
|
|
|
|
|
|||||
y0 |
2; |
2; −1 8 ) , (− |
2; |
|
2; −1 8 ) . |
|||||||||||
|
Мы не касаемся вопроса о достаточных условиях экстремума в об- |
|||||||||||||||
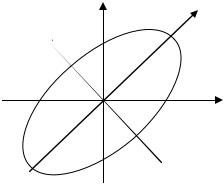
щем случае. Его исследование завело бы нас слишком далеко. Как и в случае безусловного экстремума, в практических приложениях обыкновенно заранее известно, что экстремум существует и каков его характер. Так, например, если на нашу задачу посмотреть с геометрической точки зрения (см. рис. 39.3), то мы находим на эллипсе
5x2 − 6xy + 5 y2 − 32 = 0
точки, наиболее удалённые от начала координат и наиболее близкие к нему, т.к. функция
f (x, y) = x2 + y2
это квадрат искомого расстояния.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B (−2 |
|
|
|
|
|
|
Очевидно, что в точках |
|
A ( 2 |
|
2; 2 |
|
|
2 ) и |
2; − 2 |
2 ) |
дости- |
|||||||||||
гается максимум fmax = OA = OB = 4 , |
и отрезок |
AB = 8 |
это большая ось |
||||||||||||||||||
эллипса. В точках C ( |
|
|
|
) и D (− |
|
|
|
|
|
||||||||||||
2; − |
2 |
2; 2 ) |
расстояние от начала ко- |
||||||||||||||||||
ординат до точек эллипса минимально |
fmin = OC = OD = 2 , |
и |
отрезок |
||||||||||||||||||
CD = 4 является малой осью эллипса. Более того, мы знаем направление
280
[Введите текст]
осей эллипса. Большая ось эллипса образует угол α = 450 с осью абсцисс. Таким образом, в системе координат x1Oy1 уравнение эллипса имеет вид
|
x2 |
|
y2 |
||||
|
1 |
+ |
1 |
= 1 . |
|||
16 |
4 |
||||||
|
|
||||||
Решая задачу на условный экстремум, мы «попутно» привели уравне- |
|||||||
ние эллипса 5x2 − 6xy + 5 y2 − 32 = 0 |
к каноническому виду. |
||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
x1 |
|
y1 |
|
|
|
|
A |
||
|
|
|
|
||||
D
x
C
B
Рис. 39.3
281

