9722

[Введите текст]

Pn (z) = a0 (z − z1)r1 (z − z2 )r2 L(z − zk )rk ,

где z1,K, zk – различные корни уравнения Pn (z) = 0 , а r1,K, rk – их кратности, причём r1 + K + rk = n . Указанные разложения справедливы для многочленов, как с вещественными, так и с комплексными коэффициентами.

Отметим без доказательства, что если многочлен имеет вещественные коэффициенты, то наряду с комплексным корнем z = α + iβ многочлен обладает сопряжённым корнем z = α − iβ , причём той же кратности. Объединяя в разложении многочлена такие пары, получаем

(z − z)(z − z ) = (z − α − iβ)(z − α + iβ) = z2 − 2αz + α2 + β2 = z2 + pz + q .

Таким образом, многочлен с вещественными коэффициентами раскладывается на линейные множители с вещественными корнями и квадратичные множители с парой комплексно сопряжённых корней. Переменную в случае многочлена с вещественными коэффициентами будем обозначать буквой x . Итак, многочлен с вещественными коэффициентами имеет разложение

где r1 + K + rk + 2(s1 + K + sl ) = n .

32.4. Разложение правильных дробей на простые дроби. Разложе-

ние многочлена на множители связано с задачей разложения правильной рациональной дроби

x2 + px + q не имеет действительных корней. Оказывается, что всякую правильную рациональную дробь можно представить в виде суммы конечного числа простейших дробей. Этот алгебраический факт мы примем без доказательства.

Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе ( m < n ). В противном случае ( m ³ n ) рациональная дробь называ-

230

[Введите текст]

ется неправильной. Всякую неправильную рациональную дробьможно представить в виде суммы многочлена степени m − n (целая часть) и правильной рациональной дроби, т.е.

литель на знаменатель по правилу деления многочленов. Это деление осуществим «уголком», причем делим до тех пор, пока показатель степени x в остатке не окажется меньше показателя степени x делителя.

Вид разложения дроби (32.3) определяется корнями многочлена Pn ( x) . Если знаменатель Pn ( x) имеет только действительные простые корни, то

ki ,то в разложении правильной дроби на простейшие этому корню соот-

Если знаменатель содержит множителем квадратный трехчлен x2 + px + q , не имеющий действительных корней, то при разложении на простейшие дроби этому множителю соответствует дробь вида

Mx + N

x2 + px + q

.

Если знаменатель дроби имеет кратные комплексные корни, то множителю (x2 + px + q)l с комплексно сопряженными корнями соответствуют l дробей:

[Введите текст]

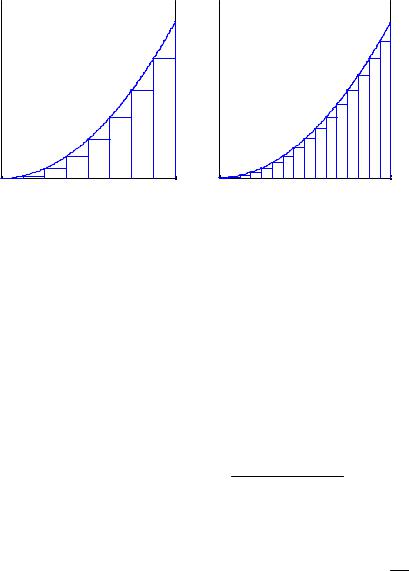
осью Ox , прямыми x = a , x = b и графиком функции, называют криволинейной трапецией. Для приближенного вычисления площади этой криволинейной трапеции разобьём промежуток [ a, b ] произвольным образом на n частей (см. рис. 33.2)

y = f ( x)

k=1

Сувеличением n точность этого приближения будет возрастать при условии, что длины всех отрезков xk будут уменьшаться. Назовем площадью

криволинейной трапеции предел последовательности Sn , если он существует и не зависит от способа разбиения и выбора точек.

33.2. Понятие определённого интеграла. Во всех приведенных выше задачах мы осуществляли следующую процедуру: брали некоторую функцию f ( x) , разбивали интервал её определения на n частей, в каждой части выбирали некоторую точку pk , составляли так называемую интегральную сумму (33.1) и, наконец, находили предел последовательности этих сумм при n → ∞ , когда длина наибольшего из отрезков дробления стремится к нулю. Получающийся при этом предел носит название определенного интеграла.

Определённым интегралом функции f ( x) на промежутке [ a, b ] на-

зывается конечный предел интегральных сумм

233

[Введите текст]

если он существует и не зависит ни от способа разбиения промежутка [ a, b ] , ни от выбора точек pk .

Ценность этого математического понятия состоит в том, что функцию f ( x) можно «наполнять» разным содержанием: это может быть функция, определяющая границу криволинейной трапеции, и тогда определенный интеграл выражает площадь трапеции, или это может быть функция, определяющая линейную плотность неоднородного стержня, и тогда определенный интеграл выражает массу стержня.

Для существования определенного интеграла функция f ( x) должна обладать некоторыми свойствами. Например, она должна быть ограниченной на [ a, b ] . В противном случае интегральную сумму за счёт выбора точек pk можно сделать как угодно большой. Оказывается, что достаточ-

ным условием существования определённого интеграла служит непрерывность f ( x) на [ a, b ] .

Теорема. Если функция f ( x) непрерывна на отрезке [ a, b ] , то определенный интеграл существует.

Примем эту теорему без доказательства.

33.3. Основные свойства определённого интеграла. Обозначение определённого интеграла было введено Лейбницем. Знак интеграла – это стилизация первой буквы латинского слова summa.

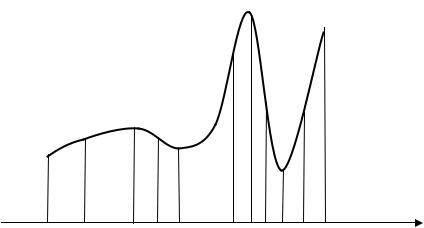
Если подынтегральная функция отрицательна на всем промежутке интегрирования или на его части, то соответствующий множитель, входящий в интегральную сумму будет отрицательным. Если интеграл интерпретировать как площадь, то части кривой, расположенной под осью абсцисс будем приписывать отрицательную площадь (см. рис. 33.3).

Если отказаться от допущения a < b и принять a > b, то в интегральной сумме все разности xk будут отрицательными. Поэтому

b a

∫ f (x)dx = −∫ f (x)dx

[Введите текст]

a

В качестве определения полагаем также ∫ f (x)dx = 0 .

∙ m(b − a) ≤ ∫ f (x)dx ≤ M (b − a), m ≤ f (x) ≤ M

a

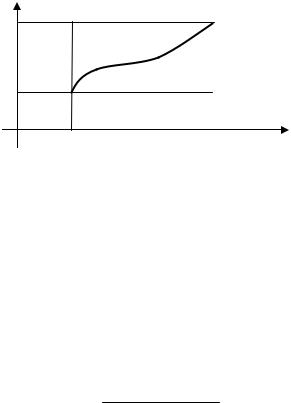
Последнее свойство проиллюстрируем рисунком (см. рис. 33.4).

y

Иногда важно не столько найти точное значение интеграла, сколько получить его оценку. Указанное неравенство геометрически соответствует тому факту, что существует прямоугольник весь расположенный внутри криволинейной трапеции и прямоугольник – содержащий эту фигуру.

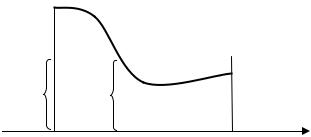
Среднее значение функции. Если даны n чисел a1, a2 , K, an , то их средним (средним арифметическим) называют число

aср = a1 + a2 +K+ an . n

Что следует понимать под средним значением функции f ( x) на отрезке [ a, b ] ? Существует, например, понятие средней плотности неоднородного тела (например, средняя плотность Земли примерно равна 5,5 ). Разделим отрезок [ a, b ] на n равных частей x1 = x2 = K = xn = (b − a) / n , возьмем в каждой части по точке Pk и составим сумму

235

[Введите текст]

Таким образом, под средним значением функции на отрезке [ a, b ] понимают отношение интеграла функции по этому отрезку к длине этого отрезка. Геометрический смысл среднего значения функции становится ясным, если его определение записать в виде

b

fср. (b − a) = ∫ f (x)dx

a

Поскольку интеграл справа выражает площадь криволинейной трапеции, то левую часть равенства можно трактовать как площадь прямоугольника. Итак, среднее значение функции равно высоте прямоугольника, в основании которого лежит отрезок [ a, b ] , равновеликого по площади криволинейной трапеции (см. рис. 33.5).

y = f ( x)

Особенно важно, что в силу непрерывности функции на отрезке [ a, b ] найдётся такая точка P0 , что fср. = f (P0 ) . Это даёт возможность выразить

значение интеграла через длину промежутка интегрирования и значение подынтегральной функции в некоторой (правда неопределённой) точке этого промежутка.

Этот результат называют теоремой о среднем в интегральном исчислении.

236

[Введите текст]

33.4. Существование первообразной функции. В предыдущей лек-

ции мы отметили, что интеграл непрерывной на [ a, b ] функции существует. Наша цель – связать понятия определённого и неопределённого интегралов и, тем самым, показать, как вычисляется определенный интеграл без вычисления интегральных сумм.

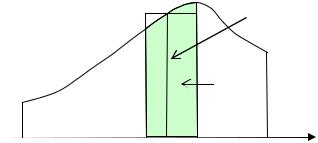
Рассмотрим интеграл с переменным верхним пределом

x

F ( x) = ∫ f (t )d t ,

a

где подынтегральная функция f ( x) непрерывна в промежутке [ a, b ] . Напомним, что переменная интегрирования – « немая», т.е. может быть обозначена любой буквой. Написанный нами интеграл – это некоторая функция F ( x) верхнего предела x , и её геометрический смысл ясен из следующего рисунка:

f (P0 )

f (x)

F

F (x)

P0

x a x x + x b

Рис. 33.6

Применяя теорему о среднем значении функции, запишем приращение

в виде

x+Δx

DF = ∫ f (t)d t = f (P0 (Dx)) × Dx ,

x

ции. Таким образом, мы пришли к замечательному факту: производная

от интеграла по переменному верхнему пределу равна значению подынтегральной функции от этого предела

237

[Введите текст]

Другими словами: это означает, что интеграл с переменным верхним пределом интегрирования является первообразной для подынтегральной функции. Этот, казалось бы, частный факт имеет принципиальное значение. Во-первых, отсюда следует, что всякая непрерывная функция имеет первообразную, а во-вторых, даже для «неберущихся» интегралов мы имеем теперь инструмент для её представления. Например, для функции

f ( x) = e− x2 среди элементарных функций нет первообразной. Теперь мы можем представить её первообразную через определённый интеграл

x

∫e−t2d t .

0

33.5. Формула Ньютона-Лейбница. Вычисление определённого интеграла как предела интегральной суммы, т.е. по формуле (33.2), – довольно сложная задача. Оказывается, что ее можно легко решить, имея одну из первообразных подынтегральной функции. Этот факт выражается основной формулой интегрального исчисления – формулой Ньютона – Лейбница

b

∫ f (x)d x = F (x) ba = F (b) − F (a) ,

a

Поскольку Φ(x) = ∫ f (t)d t = F (x) + C и Φ (a) = 0 , то C = − F (a) . Поэтому

a

x

имеем ∫ f (t)d t = F (x) − F (a) . Полагая в последнем равенстве x = b , по-

a

лучаем

b

∫ f (t)d t = F (b) − F (a) .

a

238

[Введите текст]

Лекция 34. Вычисление определённого интеграла

34.1.Интегрирование по частям и замена переменной. Пусть u ( x)

иv( x) – функции, непрерывные вместе со своими производными в промежутке [ a, b ] . Тогда функция F ( x) = u(x) × v( x) является первообразной для

своей производной

Это и есть формула интегрирования по частям в определённом инте-

грале. Как и в случае неопределённого интеграла, её целесообразно применять, если интеграл справа будет «проще», чем исходный интеграл.

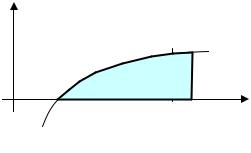
Пример. Найти площадь фигуры, ограниченной линией y = ln x , осью абсцисс и прямой x = e . Искомая площадь (см. рис. 34.1) выражает-

e

ся интегралом S = ∫ ln x d x

1

y

y = ln x

Рис. 34.1

239