9722

[Введите текст]

cij = ai1b1 j + ai 2b2 j + K + aikbkj .

Обратим внимание на то, что число столбцов первого сомножителя долж-

но равняться числу строк второго сомножителя.

где на главной диагонали стоят единицы, а все остальные элементы равны нулю, играет роль «единицы» в алгебре матриц, ибо A × E = E × A , например:

1.4. Матрицы и линейные преобразования. Для «оправдания» опре-

деления операции умножения матриц рассмотрим связь между матрицами и

линейными преобразованиями.

Пусть на плоскости задана декартова прямоугольная система координат xOy . Поставим в соответствие произвольной точке плоскости с координата-

ми (x, y) точку ( x¢, y¢) плоскости x′O′y′, координаты которой определяются следующими линейными соотношениями

x′ = a11 x + a12 yy¢ = a21x + a22 y ,

11

[Введите текст]

задающими так называемое линейное преобразование плоскости. Очевид-

но, что такое преобразование однозначно определяется его матрицей

Рассмотрим несколько примеров таких преобразований. Пусть преобразование задано следующим образом:

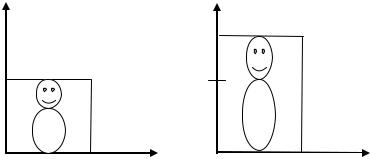
вдоль оси Oy (или к оси Ox ) с коэффициентом β > 1 (см. рис. 1.1).

y y′

β

1 1

В качестве упражнения напишите формулы преобразования, которое произвольную точку «переводит» в точку, симметричную ей относительно начала координат, и получите соответствующую матрицу.

12

[Введите текст]

Аналогичным образом можно интерпретировать линейные преобразования для трех переменных

x′ = a11x + a12 y + a13 z

′ = + +

y a21x a22 y a23 z .z′ = a31x + a32 y + a33 z

Правило умножения матриц естественным образом возникает при решении следующей задачи. Пусть линейное преобразование

преобразования, проведенные друг за другом, переводят точку (x, y) в точку

( x′′, y′′) . Очевидно, что результат этих преобразований тоже линейное преоб-

разование. Какова его матрица?

Выразим координаты точки ( x′′, y′′) через координаты исходной точки

(x, y)

Таким образом, матрица результирующего преобразования равна произведению матриц A × B исходных преобразований, взятых в соответствующем порядке, т.е.

Введенные выше матричные операции обладают следующими свойствами:

13

[Введите текст]

Лекция 2. Правило Крамера и определители матриц

Удачные обозначения обладают утончённостью и будят мысль, порой делая это, кажется почти так же, как искусный учитель.

Бертран Рассел (1872-1970гг.)

2.1. Системы двух уравнений с двумя неизвестными. Уже при ре-

шении уравнения первой степени

a × x = b

возможны три случая:

∙если a ¹ 0 , то уравнение имеет единственное решение x = b a ;

∙если a = 0 и b ¹ 0 , то уравнение не имеет решения;

∙если a = 0 и b = 0 , то уравнение имеет бесчисленное множество решений, т.к. равенство 0 × x = 0 выполняется при любых значениях x .

Оказывается, что такие же случаи имеют место при решении системы

уравнений с большим числом неизвестных. В стандартной записи система двух линейных уравнений с двумя неизвестными имеет вид

которая оба уравнения системы (2.1) обращает в тождества. В этом случае говорят, что пара чисел (α,β) «удовлетворяет» системе уравнений (2.1), а система уравнений называется совместной. Если система уравнений не имеет решений, то она называется несовместной. Эта терминология относится к системам произвольного числа уравнений.

Существует несколько способов нахождения решения системы, если оно существует. Проделаем следующие операции:

В результате получим

x(a1b2 − a2b1 ) = c1b2 − c2b1 .

15

[Введите текст]

Если число a1b2 - a2b1 ¹ 0 , то

Формулы (2.2) и (2.3) достаточно громоздки, и от их вида «в глазах рябит». Вот здесь и приходят на помощь те «удачные обозначения», о которых говорил Б. Рассел. Выпишем коэффициенты при неизвестных в виде следующей матрицы:

Для удобства в обозначение определителя включена матрица, которой он соответствует.

Вычислим ещё два определителя матриц, полученных из матрицы A путем замены ее первого и соответственно второго столбца на столбец правой части системы, т.е.

[Введите текст]

Эти формулы связаны с именем швейцарского математика Г. Крамера (1704-1752гг.). Сама идея определителя появилась ещё у Г. Лейбница

(1646-1716гг.), а название дал в 1812г. О. Коши (1789-1857гг.). Это назва-

ние довольно естественно: определители , x и y полностью опреде-

ляются системой уравнений и, наоборот, по заданным определителям (в принятых обозначениях) можно «восстановить» систему уравнений.

Исследуем полученные формулы. Будем предполагать, что не все коэффициенты при неизвестных одновременно равны нулю. В противном случае система (2.1) примет вид

хотя бы одно из чисел c1 или c2 отлично от нуля, то система (2.4) не имеет решений и называется несовместной.

Учитывая принятые обозначения для определителей, имеем два урав-

при условии, что не все входящие в эти уравнения определители равны нулю, или одно из этих уравнений, если все эти определители равны нулю.

Отсюда получаем следующие утверждения:

· если определитель ¹ 0, то система имеет единственное решение,

определяемое по формулам Крамера

y отличен от нуля, то система несовместна (пусть, для определённости,

бесчисленное множество решений: x – любое, а y выражается через x из любого уравнения исходной системы или наоборот: y – любое, а x выражается через y из любого уравнения системы.

17