
9713
.pdf
[Введите текст]
|
Δα |
|
s |
O |
Δα |
|
|
Рис. 24.2 |
|
Естественно теперь ввести понятие кривизны в данной точке как предел средней кривизны, когда длина участка s стремится к нулю
k = lim Δα = dα , s→0 s ds
т.е. кривизна равна производной угла поворота касательного вектора по длине кривой.
24.2. Вычисление кривизны плоской кривой. Для вывода форму-
лы кривизны кривой y = f (x) продифференцируем по переменной s равенство, выражающее геометрический смысл ее производной
α(s) = arctg y′x .
Пользуясь правилом дифференцирования сложной функции, получим
|
|
|
|
|
dα ds |
= |
|
|
y |
′′ |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
ds dx |
|
+ y′2 |
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dα |
|
y′′ |
||
|
|
|
′2 |
|
|
|
|
|
|
|
|
|||||
Поскольку |
ds = |
1+ y |
dx , то |
k = |
|
|
|
= |
|
. |
||||||
|
|
|
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
(1 + y′2 ) 2 |
||
Как показывает эта формула, для существования кривизны необходи- |
||||||||||||||||
мо, чтобы функция |
y = f (x) была дважды дифференцируема. Кроме того, |
|||||||||||||||
эта формула показывает, что кривая имеет |
положительную кривизну для |
|||||||||||||||
выпуклых функций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
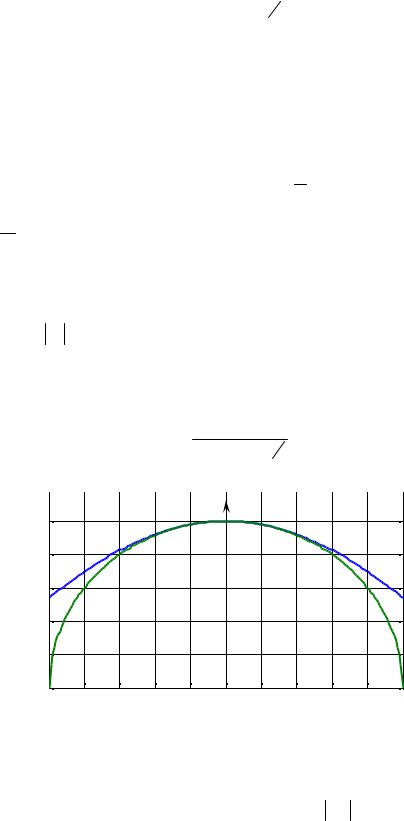
Пример. |
Найдем кривизну параболы y = x2 |
|||||||||||||||
170
[Введите текст]
k = |
2 |
. |
3 |
||
|
(1 + 4x2 ) 2 |
|
Из этой формулы видно, что при больших значениях x кривизна параболы близка к нулю, т.е. парабола «выпрямляется», а наибольшая кривизна будет в начале координат и равна 2 .
24.3. Геометрический смысл кривизны. Назовем радиусом кривиз-
ны для кривой в заданной точке величину R = 1 . Используя формулу кри- k
визны k = 1 для окружности радиуса R , дадим следующую геометриче-
R
скую интерпретацию радиуса кривизны произвольной кривой. Пусть кривизна в данной точке равна k . Через эту точку проведем окружность той же кривизны с центром на нормали к кривой в этой точке. Радиус этой окружности R = 1/ k и принимается за радиус кривизны кривой в этой точке.
На следующем рисунке приведён график функции y = cos x и соответствующая окружность. Кривизна в любой точке вычисляется по формуле
|
|
|
k (x) = |
− cos x |
3 . |
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
(1 + sin2 x) |
2 |
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
0 |
-0.8 |
-0.6 |
-0.4 |
-0.2 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
-1 |
||||||||||
Рис. 24.3
В начале координат k(0) = −1. Кривизна отрицательна, так как кривая выпукла вверх. Радиус окружности кривизны R = 1/ −1 = 1 . Центр окружно-
сти расположен в начале координат.
Свойство кривизны изменять своё значение вдоль кривой используется, например, при сопряжении прямолинейных участков железнодорожных путей с закруглениями. Допустим, что прямолинейный участок примыкает
171
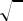
[Введите текст]
к участку, имеющему вид дуги окружности. Причем они в точке соединения имеют общую касательную, т. е. соединение гладкое. Но при движении поезда в этой точке мгновенно возникнет центробежная сила, создавая резкий толчок, что нежелательно. Поэтому такие участки соединяют с помощью некоторой переходной кривой. Вдоль неё кривизна постепенно нарастает от нулевого значения до величины обратной радиусу закругления. Аналогичная ситуация наблюдается при конструировании различного рода зубчатых зацеплений.
24.4. |
Приближённое решение уравнений. Задача точного решения |
уравнения |
f (x) = 0 для произвольной функции, как правило, неразреши- |
ма. Например, написав для уравнения x2 − 2 = 0 формулу для одного из его корней x1 = 
 2 , мы только указали математическую операцию, с помощью которой этот корень можно вычислить. Поэтому возникает необходимость приближённого вычисления корня данной функции. Обычно задают допустимую погрешность ε , с которой этот корень нужно вычислить. Это значит нужно найти такой промежуток [a,b] , содержащий корень ξ ( f (ξ) = 0 ), что его длина b − a < ε. Предполагается, что вычисление значе-
2 , мы только указали математическую операцию, с помощью которой этот корень можно вычислить. Поэтому возникает необходимость приближённого вычисления корня данной функции. Обычно задают допустимую погрешность ε , с которой этот корень нужно вычислить. Это значит нужно найти такой промежуток [a,b] , содержащий корень ξ ( f (ξ) = 0 ), что его длина b − a < ε. Предполагается, что вычисление значе-
ний функции |
f (x) проблемы не составляет. |
|
Рассмотрим несколько методов поиска корней на примере уравнения |
||
|
f (x) = x3 + x −1= 0 . |
|
Функция f (x) всюду непрерывна. Вычислив f (0) = -1 < 0 и |
f (1) =1 > 0 , |
|
убеждаемся, |
что в промежутке [ 0,1] есть, по крайней мере, |
один корень |
нашего уравнения. Покажем, что других корней в этом промежутке нет.
′ |
2 |
+1 |
> 0 положительна, поэтому график |
Производная функции f (x) = 3x |
|
функции один раз пересечёт ось Ox , переходя от отрицательного значения к положительному значению. Иногда эту процедуру «отделения» корня
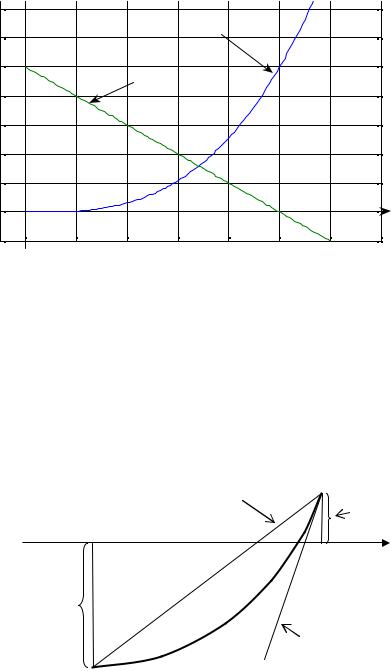
производят графически. Построим графики функций |
y = x3 |
и |
y |
2 |
= 1 − x . |
|
1 |
|
|
|
Абсцисса точки их пересечения и есть искомый корень (см. рис. 24.4). В нашем случае из рисунка видно, что корень расположен в промежутке 0,6 < ξ < 0,8 , т. е. мы ещё сузили промежуток, где находится корень. Далее применим так называемый метод деления отрезка. Вычисляем значение
функции в средине отрезка |
f (0,7) = 0,343 - 0,300 |
= 0,043 > 0 и |
на одном |
из его концов, например, |
f (0,6) = 0,36 ×0,6 - 0, |
4 = -0,184 < 0 . |
Следова- |
тельно, корень находится в промежутке 0,6 < ξ < 0,7 , т. е. корень вычислен с точностью до 0,1. Ясно, что эту процедуру уточнения значения корня можно продолжить, но она требует слишком большого количества вычислений.
172
[Введите текст] |
|
|
|
|
|
|
|
1.4 |
|
|
|
y=x3 |
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0.8 |
|
y=1-x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-0.2 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
0 |
|||||||
Рис. 24.4
Познакомимся с методами, которые быстрее ведут к цели. Но для их применения нужна дополнительная информация о поведении функции в промежутке, на котором изолирован корень. Заметим, что вторая произ-
водная функции |
′′ |
положительна, следовательно, |
график |
||
f (x) = 6x > 0 |
|||||
функции в промежутке 0,6 < x < 0,7 имеет вид (см. рис. 24.5) |
|
||||
|
|
|
B |
|
|
|
|
хорда |
|
||
|
a = 0.6 |
|
f (b) = 0.043 |
||
|
|
|
|
|
|
|
|
|
b = 0.7 |
|
|
|
|
f (x) |
|
||
f (a) = −0.184 |
|
|
|
|
|
|
|
|
касательная |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Рис. 24.5 |
|
|||
Если провести хорду АВ , то точка |
a1 пересечения хорды с осью |
Ox даст |
|||
очередное приближение к искомому корню слева. Приближение справа можно получить, найдя точку пересечения b1 касательной (проходящей через точку В ) с осью Ox . Запишем уравнение хорды АВ как уравнение прямой, проходящей через две точки
y − f (a) |
= |
x − a |
, |
f (b) − f (a) |
|
||
|
b − a |
||
173 |
|
|
|

[Введите текст]
которое в данном случае примет вид
y + 0,184 = x − 0, 6 . 0, 227 0,1
Отсюда при y = 0 получаем a1 ≈ 0,681. Уравнение касательной в точке В имеет вид
y − f (b) = f ′(b)(x − b)
или
y − 0,043 = 2,47(x − 0,7) .
Полагая y = 0 , получаем b1 ≈ 0,683 . Проверим, не «потеряли ли» мы ко-
рень, взяв приближенные значения |
a1 и b1 . Для этого подсчитаем значе- |
ния функции в этих приближённых значениях |
|
f (0,681) = −0,003K< 0, |
f (0,683) = 0,002K> 0 . |
Значения функции на концах промежутка [0,681; 0,683] оказались разных знаков. Значит, мы вычислили корень с точностью ε = 0,002 . Если же в качестве приближённого значения корня взять среднее арифметическое
ξ = (a1 + b1 ) / 2 = 0, 682 , то корень будет вычислен с точностью ε = 0,001.
f ′ > |
0 |
f ′ < 0 |
|
f ′′ > 0 |
|||
f ′′ > |
0 |
||
|
|||
a |
|
b |
a
b
f ′ < 0
f ′ > 0 f ′′ < 0 f ′′ < 0
a |
b |
b |
a |
Рис. 24.6
174
[Введите текст]
Эту процедуру уточнения корня методом хорд и касательных можно продолжить, однако с методом касательных нужно быть внимательнее. Построив касательную не в той точке промежутка, можно не приблизиться к корню, а удалиться от него (см. рис 24.6). На рисунке хорды проведены пунктирной линией. Анализ возможных ситуаций показывает, что касательную нужно проводить из той точки кривой y = f (x) , в которой знак функции совпадает со знаком второй производной.
175
[Введите текст]
Раздел 5. Аналитическая геометрия. Кривые и поверхности второго порядка
Лекция 25. Линии второго порядка
До сих пор в аналитической геометрии мы изучали прямые и плоскости, в уравнения которых переменные x , y и z входят в первой степени. Сейчас переходим к рассмотрению кривых на плоскости, задаваемых более сложными алгебраическими уравнениями, включающими вторые степени текущих координат x и y или их взаимное произведение.
Уравнение вида
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 |
(25.1) |
называется общим уравнением линии (кривой) второго порядка. В нём коэффициенты A , B , C , D , E и F — любые действительные числа, для
которых A2 + B2 + C 2 ¹ 0 , т.е. по крайней мере, одно из чисел A , |
B или |
C отлично от нуля. Например, уравнение x2 + xy + y2 - y - 5 = 0 |
отно- |
сится к классу уравнений второго порядка и получается из общего вида (25.1) при конкретном значении коэффициентов.
Простейшим примером кривой, задаваемой уравнением (25.1), является окружность. Окружность определяется как множество точек плоскости, равноудалённых от заданной точки (центра). Вводим на плоскости прямоугольную декартову систему координат, совместив её начало с центром окружности. Координаты произвольной точки M , лежащей на окружно-
сти, |
обозначим x и y . Эти координаты связаны между собой равенством |
x2 + |
y2 = R2 , которое и представляет собой уравнение окружности. Ему |
удовлетворяют координаты каждой точки окружности и не удовлетворяют координаты любой другой точки плоскости, не лежащей на ней. Видим, что это уравнение является уравнением второго порядка.
К другим линиям, задаваемым уравнением (25.1), относятся эллипс, гипербола и парабола. В некоторых случаях получаются пара пересекающихся или параллельных прямых, одна прямая или точка. Изучение этих классических линий мы, как и для окружности, будем начинать с их определения. Дальше будем ставить задачу вывести уравнение, которому удовлетворяют координаты точек в том и только том случае, когда точки лежат на рассматриваемой линии. Для получения уравнения будем вводить систему координат, располагая её по отношению к линии так, чтобы уравнение в этой системе имело простейший вид, называемый каноническим уравне-
нием линии.
176
[Введите текст]
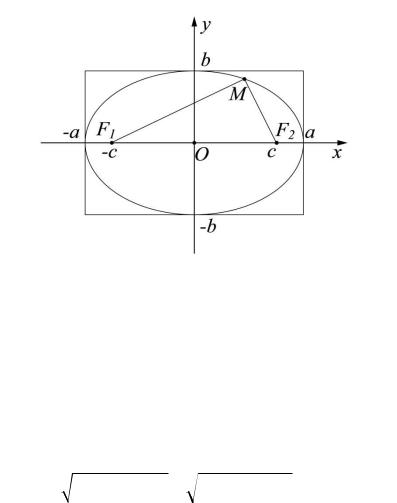
25.1. Эллипс. Эллипсом называется множество всех точек M плоскости, сумма расстояний каждой из которых до двух данных точек F1 и F2 есть величина постоянная (её принято обозначать 2a ). В этих обозначениях можно коротко записать определение эллипса в виде равенства MF1 + MF2 = 2a . Точки F1 и F2 называются фокусами эллипса. Расстояние F1F2 между фокусами обозначают 2c .
Из определения непосредственно вытекает способ построения: если концы нерастяжимой нити длины 2a закрепить в точкахF1 и F2 , затем натянуть нить остриём карандаша, то при движении острия оно будет вычерчивать выпуклую замкнутую линию (овал). Сумма расстояний от произвольной точки M до двух фиксированных точек F1 и F2 не может быть меньше расстояния между точками F1 и F2 : MF1 + MF2 ³ F1F2 . Будем предполагать, что это неравенство строгое, т.е. 2a > 2c или a > c .
Выведем теперь уравнение эллипса. Для этого введём прямоугольную декартову систему координат. В качестве оси абсцисс мы возьмём прямую, проходящую через F1 и F2 , считая её направленной от F1 к F2 , начало системы координат поместим в середине отрезка F1F2 (рис. 25.1).
Рис. 25.1
В этой системе координат для произвольной точки M координаты обозначим через x и y . Фокусы, оказавшись теперь на оси Ox симмет-
рично относительно начала, будут иметь координаты F1 (−c;0) и F2 (c;0) .
Расстояния MF1 и MF2 между точками заменим их выражениями через координаты. Получим

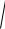 ( x + c )2 + y2 +
( x + c )2 + y2 + 
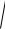 ( x − c )2 + y2 = 2a .
( x − c )2 + y2 = 2a .
177

[Введите текст]
По существу, это соотношение представляет собой уравнение эллипса. Ему удовлетворяют координаты точек в том и только том случае, когда точки лежат на эллипсе. Проведём алгебраические преобразования, упрощающие эту запись. Для этого уединим в уравнении первый радикал, возведём в квадрат обе части полученного равенства
( x + c )2 + y2 = 4a2 − 4a
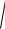 ( x − c )2 + y2 + ( x − c )2 + y2
( x − c )2 + y2 + ( x − c )2 + y2
и приведём его к виду a
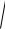 ( x − c )2 + y2 = a2 − cx . Возведя в квадрат обе части последнего равенства, найдём
( x − c )2 + y2 = a2 − cx . Возведя в квадрат обе части последнего равенства, найдём
(a2 − c2 ) x2 + a2 y2 = a2 (a2 − c2 ) .
Мы отмечали, что a > c , значит a2 − c2 > 0 , и можно ввести в рассмотрение
новую величину b = 
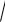 a2 − c2 (при этом b < a ). Тогда уравнению можно придать вид b2 x2 + a2 y2 = a2b2 или
a2 − c2 (при этом b < a ). Тогда уравнению можно придать вид b2 x2 + a2 y2 = a2b2 или
|
x2 |
+ |
y2 |
= 1. |
(25.2) |
|
a2 |
|
|||
|
|
b2 |
|
||
Это уравнение называется каноническим уравнением эллипса. Осо- |
|||||
бенностью уравнения является то, что оно содержит x и |
y только в чёт- |
||||
ных степенях, поэтому если точка ( x, y ) принадлежит эллипсу, то ему принадлежат и точки ( x;− y ), (−x; y ), (− x, − y ). Отсюда следует, что эллипс симметричен относительно осей Ox и Oy , также относительно начала координат. Оси симметрии эллипса называются его осями, а точка пересечения осей – центром эллипса. Точки, в которых эллипс пересекает свои оси, называются его вершинами. Положив y = 0 в уравнении (25.2), най-
дём две вершины A1 (−a;0) и A2 (a;0) на оси Ox . Положив x = 0 , найдём две точки пересечения эллипса с осью Oy : B1 (0; −b) и B2 (0;b) (рис. 25.1).
Итак, эллипс имеет четыре вершины A1, A2 , B1, B2 , которые ограничивают на осях отрезки A1 A2 = 2a и B1B2 = 2b (эти отрезки тоже принято называть осями эллипса), а ОA1 = a и ОB1 = b называются соответственно большой
и малой полуосями эллипса.
Исследовав форму эллипса путём анализа его канонического уравнения, можно теперь непосредственно построить в первой четверти график
функции y = |
b |
|
|
и, отразив его симметрично относительно осей |
|
|
a2 − x2 |
||||
a |
|||||
|
|
|
|
координат, получить овальную замкнутую кривую, изображённую на ри-
178
[Введите текст]
сунке 25.1. Отметим, что при этом все точки эллипса лежат внутри прямоугольника, образованного прямыми x = a , x = −a , y = b , y = −b .
Введём ещё одну величину, характеризующую форму эллипса. Отношение ε расстояния между фокусами эллипса к длине его большой оси на-
зывается эксцентриситетом эллипса: ε = |
c |
. |
Величина эксцентриситета |
||||||||||||||||||||
|
|||||||||||||||||||||||
0 < ε < 1 , так как |
|
a > c > 0 . |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Поскольку |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
− b2 |
b 2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
c2 |
|
a2 |
b 2 |
b |
|
|
|
|
|
|||||||||||
|
2 |
|
|
= |
1 − ε |
2 |
|
||||||||||||||||
ε |
|
= |
|
|
= |
|
|
|
= 1 − |
|
, то ε = |
1 − |
|
, |
|
|
. |
||||||
|
a |
2 |
|
a |
2 |
|
|
a |
|
||||||||||||||
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
||||||||||
Видим, что эксцентриситет определяется соотношением осей эллипса. В случае ε = 0 (если a = b ) эллипс превращается в окружность с уравнением x2 + y2 = a2 . Чем ближе эксцентриситет к единице, тем меньше отноше-
ние b и тем больше эллипс вытянут. a
25.2. Гипербола. Множество всех точек M плоскости, разность расстояний которых до двух данных точек F1 и F2 есть величина постоянная, называется гиперболой. Указанная разность берётся по абсолютному значению и обозначается 2a . Точки F1 и F2 называются фокусами гиперболы. Как и ранее, 2c = F1F2 - расстояние между фокусами. Таким образом, если точка M гиперболы находится ближе к фокусу F2 (рис. 25.2), выполняется равенство MF1 − MF2 = 2a , а если M находится ближе к фокусу F1 , то MF2 − MF1 = 2a . Из рассмотрения суммы длин сторон треугольника
MF1F2 видим, что MF1 < MF2 + F1F2 |
и MF2 < MF1 + F1F2 . Поэтому, в зави- |
симости от расположения точки |
M по отношению к фокусам, |
MF1 − MF2 < F1F2 или MF2 − MF1 < F1F2 . В наших обозначениях получаем 2a < 2c или a < c .
Для получения уравнения вводим систему координат так, чтобы фокусы F1 и F2 лежали на оси Ox , а начало координат совпадало с серединой отрезка F1F2 (рис. 25.2). В этой системе координаты произвольной точки M обозначим x и y , а координаты фокусов будут соответственно:
F1 (−c;0), F2 (c;0) . Заменив расстояние MF1 и MF2 между точками их вы-
ражениями через координаты, получим

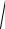 ( x + c )2 + y 2 −
( x + c )2 + y 2 − 
 ( x − c )2 + y 2 = ±2a .
( x − c )2 + y 2 = ±2a .
179
