
9531
.pdf
tnab tkr ( ) , то гипотеза принимается, что говорит о незначимости выборочного ко-
эффициента корреляции, мало отличного от нуля. Если же tnab tkr ( ) , то гипотеза
отвергается, то есть выборочный коэффициент корреляции, а значит и уравнение регрессии, значимы. Значимость коэффициента корреляции говорит о том, что полученный по данной выборке коэффициент неслучайно отличен от нуля, а корреляционная зависимость между наблюдаемыми величинами существенна.
Аналогично строится критерий Фишера для проверки гипотезы H 0 {R 2 0} о значимости коэффициента детерминации R 2 :
если |
|
Fnab Fkr ( ) , то гипотеза H 0 |
принимается, т.е. R 2 незначим. |
||||
Выводы критериев значимости rxy |
и R 2 идентичны [9]. |
||||||
|
Значимость коэффициентов регрессии может быть оценена по критериям Стью- |
||||||
дента |
|
a |
tn 2 , |
b |
tn 2 . |
|
|
|
Sa |
|
|
||||
|
|
|
|
||||
|
|
|
Sb |
|
|
||
|
|
|
3. О множественной |
регрессии |
|||
|
На практике, объясняемая переменная Y часто зависит не от одной, а несколь- |
||||||
ких объясняющих переменных |
Х к . Пусть таких переменных будет m 1, и они |
||||||
наблюдаются вместе с переменной Y в многофакторной выборке ( yi x1i , x2i ,..., xmi ) объема n. Построим выборочную линейную регрессию в форме:
уˆ(x1 , x2 ,...xm ) b0 |
b1 х1 |
b2 x2 ..... bm xm e . |
|
||||
|
|
|
|
|
|
|
(b0 , b1 ,b2 ,.....bm )Т , то ее |
Если введем следующие |
вектора |
x (1, x1 , x2 |
,...xm ) , b |
||||
|
|
|
|
|
|
|
|
можно записать в векторном виде: |
yˆ(x) x |
b . |
|
|
|||
|
|
|
Х , |
|
|
|
|
Введем матрицу |
измерений |
вектор |
измерения y и переменных |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
xi (1, x1i , x2i ,...xmi ) , а так же вектор регрессии y : |
|
||||||
1
1
Х...
1
x11 x12
...
x1n
x21 x31 ...
x22 x32 ...
... ... ...
x2n x3n ...
x
m1
xm2
... ,
xmn
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
||
y |
, |
х |
i |
||
|
... |
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
xi1xi 2
...
xin
|
|
yˆ1 |
|
|
|
|
|
|
|
|
|
yˆ 2 |
|
|
, |
ˆ |
|
|
, |
y |
... |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
yˆ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда вектор регрессии будет |
ˆ |
X b |
|
|
|
|
|
ˆ |
||||||
y |
, а ошибки регрессии e y y . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим оценки коэффициентов регрессии b методом наименьших квадратов, |
||||||||||||||
для чего рассмотрим суммарную ошибку регрессии |
|
|
|
|||||||||||
2 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei |
e |
|
|
ˆ |
T |
|
ˆ |
|
|
T |
( y |
X b ) . |
|
|
e ( y y) |
|
( y y) ( y X b ) |
|
|
|
|||||||||
i 1
91

Подберем такие коэффициенты b , при которых суммарная ошибка регрессии минимальна, для этого рассмотрим условие минимума:
|
n |
2 |
|
T |
|
T |
|
|
|
|
|
|
|
|
|
||||||
|
ei |
2 ( X |
|
y X |
|
X b) 0 , |
|
в |
( X T X ) 1 ( X T y) . |
|
b i 1 |
|
|
|
|
|
|
|
|
|
|
Таким образом, оценка для коэффициентов регрессии - построена. Матрица, входящая в выражение для коэффициентов имеет вид средних перекрестных произведений:
|
1 |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
x |
|
|
... |
|
|
x |
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
m |
|
|
|
|
|
|
x1 |
|
|
x1 x1 |
|
|
x1 x2 |
|
|
x1 x3 |
... |
|
x1 xm |
|
|
|
|
|||||||||||||
Х T X n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|||||
x |
2 |
|
x |
x |
|
x |
2 |
x |
2 |
|
x |
2 |
x |
3 |
... |
x |
2 |
x |
|
, |
|||||||||
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||||||||||
... |
|
|
|
... |
|
|
|
... |
|
|
|
|
... |
|
... |
|
|
... |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xm x1 |
|
xm x2 |
|
xm x3 |
... |
|
|
|
|
|
|
|
|
||||||||||||
xm |
|
|
|
xm xm |
|
|
|||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
yx |
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
X |
T |
n |
|
yx |
|
|||||
|
y |
|
2 |
|
. |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
... |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
yxm |
||||||
|
|
Значимость построенного уравнения линейной среднеквадратической регрессии |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
yˆ(x) |
x |
b проверяется |
по значимости коэффициентов регрессии bк |
или коэффи- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
||
циента детерминации |
R2 |
|
|
Y |
1 |
e |
. |
Для проверки вычисляются: |
De |
|
ei2 - |
|||||||||||||||||||
D |
|
n |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
y |
|
|
|
|
|
|
|
|
|
i 1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
||
дисперсия |
ошибок регрессии, |
S 2 |
|
|
|
|
ei2 - несмещенная стандартная ошибка |
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
n m |
1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|||||||
регрессии, |
Sb2 |
S 2 |
Wкк1 - несмещенные дисперсии коэффициентов регрессии. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Для построения критериев значимости воспользуемся известными статистика- |
|||||||||||||||||||||||||||
ми: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
bk |
t |
|
|
~ распределение Стьюдента с n m 1степенями свободы, |
|
|
|
||||||||||||||||||||||
|
|
n m 1 |
|
|
|
|||||||||||||||||||||||||
|
Sb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R 2 |
|
n m 1 |
F , |
|
~ F-распределение Фишера с m, |
|
|
n m 1 степеня- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 R 2 |
|
|
m |
|
|
|
||||||||||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|||||||
ми свободы. Задаваясь уровнем значимости проверяемой гипотезы H 0 |
{bk |
0} , со- |
||||||||||||||||||||||||||||
ответствующей |
независимости величин |
Х r и Y , можно сравнить наблюдаемое зна- |
||||||||||||||||||||||||||||
чение критерия tnab с критическим значением tkr ( ) . Если |
|
tnab |
|
|
tkr ( ) , то гипотеза |
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
принимается, что говорит о незначимости |
коэффициента |
bк , мало отличного от ну- |
||||||||||||||||||||||||||||
ля, то есть о незначимости переменной Х r |
в уравнении регрессии, такие переменные |
|||||||||||||||||||||||||||||
желательно исключить из модели регрессии. Аналогично проверяется гипотеза о значимости коэффициента детерминации H 0 {R 2 0} , соответствующей значимости
всего уравнения регрессии в целом. Сравнивая наблюдаемое значение критерия Fnab ,
с критическим значением Fkr ( ) , можно утверждать, что если |
Fnab Fkr ( ) , то гипо- |
теза принимается, что говорит о незначимости коэффициента |
R 2 , мало отличного |
от нуля, то есть о не значимости уравнения регрессии в целом. |
|
92
Помимо значимости построенного уравнения регрессии, его качество оценивается так же отсутствием зависимости между объясняющими переменными Х r (мультиколлинеарности), отсутствием зависимости величины дисперсии ошибок De от переменных Х к и Y (гетероскедастичности), отсутствием зависимости ошибок ei yi yˆi между собой (например, автокорреляции).
Мультиколлинеарность приводит к неустойчивости обращения матрицы W, а ее устранение возможно путем исключения из регрессионной модели малозначимых и сильнозависимых объясняющих переменных (факторов). Для такого исключения
построим |
|
|
|
корреляционную |
матрицу парных |
|
коэффициентов корреляции: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
xi x j |
|
|
|
|
|
j |
. Тогда, если |
|
|
|
|
|||
xi |
x |
r |
1 , а коэффициент b |
|
незначим или малозначим, то |
||||||||||
|
|
|
|
|
|
|
|
к |
|||||||
ij |
x |
x |
|
|
|
|
iк |
|
|
||||||
|
|
j |
|
|
|
|
|||||||||
|
|
|
|
i |
|
|
|
|
|
||||||
переменную Х к можно исключить из модели регрессии, если коэффициент детерминации при этом значимо не уменьшается.
Гетероскедастичность и автокорреляция могут быть установлены при помощи теста ранговой корреляции Спирмена и теста Дарбина-Уотсона соответственно [1]. Влияние этих нежелательных для качества регрессии факторов может быть ослаблено путем различного рода преобразования переменных регрессионной модели [9].
3. О нелинейной регрессии
Иногда линейная модель регрессии бывает недостаточной, с точки зрения ее качества и значимости, поэтому может быть использованы нелинейные модели. В простейшей форме нелинейность может быть учтена путем введения инструментальных
переменных zr r (xk ) , которые входят в модель регрессии обычным линейным
образом. При этом часто |
используются степенная функция zr x , логарифмическая |
zr ln x , показательная |
zr e x и иногда тригонометрическая zr Sin( x 0 ) для |
выявления циклических факторов в зависимостях. Например, нелинейная модель 2- го порядка может быть построена следующим образом (рис. 15.3):
уˆ(x) b0 b1 х b2 x |
2 |
e |
|
ˆ |
b1 х b2 z2 e , |
|
у(x, z2 ) b0 |
где z2 x 2 - инструментальная переменная. Введение новых членов в модель регрессии, в том числе и инструментальных, оправдано тогда, когда значимо повышается коэффициент детерминации.
93
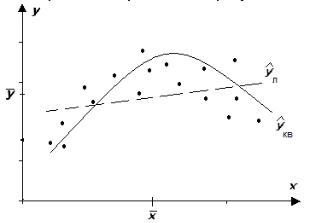
Рис.15.3 Кривая нелинейной среднеквадратической регрессии 2-го порядка.
Иногда |
строится |
мультипликативная |
модель |
регрессии |
уˆ(x1 , x2 ,...xm ) b0 х1b1 x2b2 |
.... xmbm e , которая путем |
логарифмирования может |
||
быть сведена к обычной аддитивной линейной модели для инструментальных переменных.
94
95
96
97

98

99
|
СОДЕРЖАНИЕ |
|
|
ТЕОРИЯ ВЕРОЯТНОСТЕЙ |
|
Введение |
|
3 |
Лекция 1. |
Предмет теории вероятности |
4 |
Лекция 2. |
Вычисление вероятностей |
11 |
Лекция 3. |
Вероятности сложных событий |
17 |
Лекция 4. |
Схема независимых испытаний |
25 |
Лекция 5. |
Дискретные случайные величины |
31 |
Лекция 6. |
Непрерывные случайные величины |
36 |
Лекция 7. |
Примеры непрерывных случайных величин |
43 |
Лекция 8. |
Числовые характеристики величин |
50 |
Лекция 9. |
Закон больших чисел |
58 |
|
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА |
|
Лекция 10. Выборочный метод математической статистики |
63 |
|
Лекция 11. Выборочные распределения |
69 |
|
Лекция 12. Статистические оценки параметров распределения |
72 |
|
Лекция 13. Проверка статистических гипотез |
78 |
|
Лекция 14. Примеры построения критериев проверки |
82 |
|
Лекция 15. Элементы корреляционного анализа |
90 |
|
Приложения |
98 |
|
Литература |
104 |
|
100
