
9480
.pdf69
Если при этом все силы системы лежат в одной плоскости Oxy, то и уравнение (в) также обратится в тождество и в системе останется два уравнения:
|
∑ |
|
= 0 |
{ |
=1 |
|
(8.7) |
∑ |
|
||
|
|
= 0 |
|
|
=1 |
|
|
СИСТЕМЫ ПАР СИЛ
Если система сил состоит только из пар, для каждой из которых, как известно, сумма векторов сил равна нулю, то уравнения проекций сил (а,б,в) в (7.4) оказываются тождествами.
Тогда для системы пар остаются только уравнения сумм проекций моментов пар, которые были записаны нами как уравнения (8.8):
mix 0, |
|
|
|
|
|
miy |
0, |
(8.8) |
|
|
|
miz |
0. |
|
Если при этом все силы системы лежат в одной плоскости, то равновесие системы описывается одним уравнением:
n |
|
mi 0. |
(8.9) |
i 1
СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
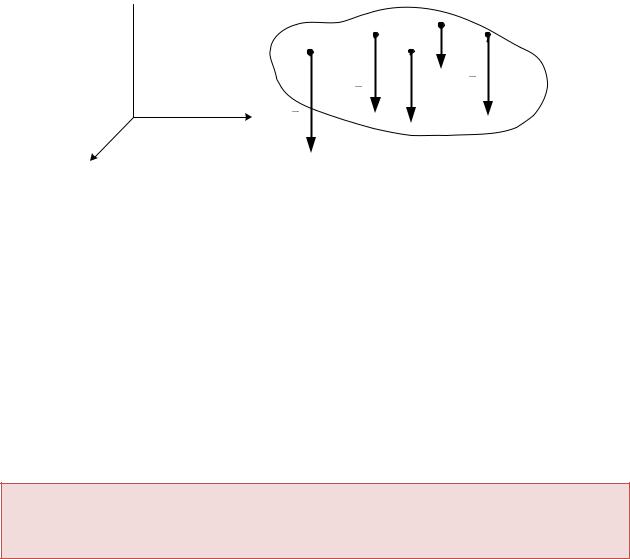
Пусть линии действия всех сил параллельны друг другу (рис. 8.4). Направим ось z параллельно этим силам. В этом случае являются тождествами уравнения проекций сил на оси х и у, а также уравнения моментов сил относительно оси z, то есть уравнения (а,б,е) из (8.3).
Тогда остаются три уравнения:
70
 z
z
|
Fn |
|
O |
F2 |
|
F1 |
||
|
||
|
y |
x
|
|
|
|
|
|
Рис. 8.4 |
|
∑ |
|
= 0 |
|
|
|
|
|
=1 |
|
|
|
|
|
∑ |
|
|
|
= 0 |
(8.10) |
|
=1 |
( ) |
|
|||
|
|
|
|
|
|
|
|
∑ |
|
|
|
= 0, |
|
{ |
=1 |
( ) |
|
|||
|
|
|
|
|
||
которые называются уравнениями равновесия пространственной
системы параллельных сил.
Тема 9.
ЦЕНТР ТЯЖЕСТИ
9.1. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
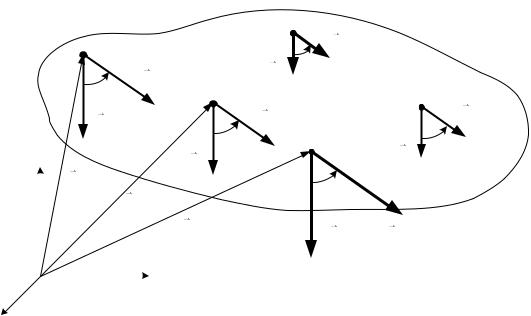
Рассмотрим систему (рис. 9.1) параллельных и одинаково направленных сил ( 1, 2, … , ) приложенных к твердому телу в точках
O1,O2 ,...,On .
Пусть эта система сил имеет равнодействующую которая имеет то же направление, что и силы системы.
По модулю она равна
RFi
i 1n
Пусть единичный вектор указывает направление сил системы. Тогда силы можно записать в виде:
71
|
= , |
|
= , … , |
|
= , |
|
|
|
|||
1 |
1 |
2 |
2 |
|
|
= .
Изменим направление сил системы. Для этого с помощью единичного
вектора укажем новое направление (рис. 9.1).
′
Тогда все силы системы повернутся на один и тот же угол α и образуется новая система параллельных сил:
|
|
|
|
… , |
|
|
′ |
= ′ ′, |
′ |
= ′, |
′ |
= ′, |
|
1 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
′ = ′. |
|
|
|
|
|
|
Модули сил при этом не изменятся.
Такая операция называется поворотом системы параллельных сил.
Покажем, что имеется такая точка C , через которую линия действия равнодействующей пройдет при любом направлении сил системы.
Согласно теореме Вариньона, момент равнодействующей системы сил относительно любой точки равен сумме моментов всех сил системы относительно этой точки.
В рассматриваемом случае, например,
|
|
= |
∑ |
|
|
|
|
|
|
∑ |
|
( |
|
|
|||
() |
=1 |
|
( ) или |
× = |
=1 |
× ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Где |
, |
, … , |
|
|
— радиус-векторы точек O ,O ,...,O |
, проведенные из начала |
|||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
n |
|
|
координат (точки O ), |
— радиус-вектор точки С. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим в последнем равенстве все векторы сил через единичный |
|||||||||||||||||
вектор, после чего оно примет следующий вид: |
|
|
|
||||||||||||||
|
|
|
× = |
∑ |
( × ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
или |
|
|
× = |
∑ |
( ) × . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
Чтобы это равенство выполнялось при любом по направлению единичном векторе должны быть равны сомножители этого вектора в левой и правой частях, т. е.
|
= ∑ |
|
( ). |
|||
|
|
=1 |
|
|
|
|
откуда получаем: |
|
|
|
|
|
|
|
|
∑ |
|
|
||
|
= |
|
|
|
|
(9.1) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72
Точка С, через которую линия действия равнодействующей пройдет при любом повороте системы параллельных сил, называется центром параллельных сил.
Формула (9.1) определяет положение центра параллельных сил через его радиус-вектор.
Координаты центра параллельных сил можно получить, если спроектировать равенство (9.1) на координатные оси:
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
F1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
F2 |
|
Fn |
|
|
|
1 |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
Fn |
|
r1 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
rC |
R |
R |
|
|
|
|
|
|
|
|
|
|
||
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.1 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
xi Fi |
|
|
|
|
|
|
|
x |
|
|
i 1 |
, |
|
|
||||
|
|
|
|
|
|
||||||
|
|
C |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
yi Fi |
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
(9.2) |
|
|
yC |
|
|
|
|
, |
|
||||
|
|
|
R |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
zi Fi |
|
|
|
|
|
|
|
z |
|
i 1 |
|
. |
|
|
||||
|
|
|
|
|
|
||||||
|
|
C |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что формулы (9.1) и (9.2) справедливы и для случая параллельных сил, направленных в разные стороны, если в них полагать величины Fi для сил одного направления со знаком «плюс», а для сил другого направления со знаком «минус».
73
9.2. ЦЕНТР ТЯЖЕСТИ
Силы притяжения отдельных частиц тела к Земле направлены к центру Земли. Поскольку размеры рассматриваемых тел малы по сравнению с радиусом Земли, эти силы можно считать параллельными.
Равнодействующая этих параллельных сил — это сила тяжести (ее модуль — это вес тела), а центр этой системы параллельных сил (в котором всегда приложена сила тяжести) называется центром тяжести тела.
Поворот тела относительно Земли приводит к повороту системы сил относительно самого тела. При этом положение центра тяжести тела не зависит от расположения тела в пространстве.
Если обозначить модули сил тяжести отдельных частей тела
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
и вес тела |
G |
G |
, то радиус-вектор и координаты центра |
|||||||||||
( |
, , … , |
) |
|
|
|
|
i |
|||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
тяжести могут быть вычислены по общей формуле |
||||||||||||||
|
|
|
|
= |
|
∑ |
|
, |
|
(9.3) |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из которой следует, что |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
xiGi |
|
|
|
|
||||
|
|
|
x |
|
|
i 1 |
|
|
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
C |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
yiGi |
|
|
|
|
||||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
(9.4) |
||
|
|
|
yC |
|
|
|
|
, |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ziGi |
|
|
|
|
||||
|
|
|
z |
|
|
i 1 |
. |
|
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
C |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если тело однородное, т. е. все его части имеют один и тот же удельный вес g , где g − ускорение свободного падения, а −
n
плотность, то G V и Gi Vi , где V Vi − объем всего тела, а Vi −
i 1
объем i - ой его части.
После подстановки этих выражений в формулы (9.4) и сокращения мы получаем соотношения для координат центра тяжести объема:
74
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xiVi |
|
|
|
|
x |
|
|
|
i 1 |
, |
|
||
|
|
|
|
|||||
|
C |
|
|
V |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
yiVi |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
(9.5) |
yC |
|
|
|
|
, |
|||
|
V |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ziVi |
|
|
|
|
z |
|
|
i 1 |
|
. |
|
||
C |
V |
|
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр тяжести однородной пластины (плиты) постоянной толщины может быть вычислен аналогично через площади отдельных ее частей Ai и
n
общую площадь A Ai :
i 1
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi Ai |
|
|
|
|
x |
|
|
i 1 |
, |
|
|||
|
|
|
||||||
|
C |
|
|
A |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
yi Ai |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
(9.6) |
yC |
|
|
|
|
, |
|||
|
A |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zi Ai |
|
|
|
|
z |
|
i 1 |
|
. |
|
|||
|
|
|
||||||
|
C |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если при этом вся пластина лежит в одной плоскости, например в плоскости Oxy), то третье уравнение в (9.6) обращается в тождество и центр тяжести определяется по формулам
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
xi Ai |
|
|
x |
|
|
i 1 |
, |
||
|
|
|||||
|
C |
|
|
A |
(9.7) |
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
yi Ai |
|
|
|
y |
|
|
|
|
||
|
i 1 |
|
. |
|||
|
|
|||||
|
C |
|
|
A |
|
|
|
|
|
|
|
|
|
Центр тяжести однородного пространственного ломаного стержня, состоящего из ряда прямолинейных участков, определяется через длины его
n
участков Li и общую длину L Li :
i 1

75
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi Li |
|
|
|
|
x |
|
i 1 |
, |
|
|||
|
|
||||||
|
C |
|
L |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
yi Li |
|
|
|
|
|
|
|
i 1 |
|
|
|
(9.8) |
yC |
|
|
|
, |
|||
L |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zi Li |
|
|
|
|
z |
|
i 1 |
|
. |
|
||
|
|
|
|||||
|
C |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТЕМЫ ЛЕКЦИЙ РАЗДЕЛА «КИНЕМАТИКА»
Тема 1:
КИНЕМАТИКА ТОЧКИ
1.1. ВВЕДЕНИЕ В КИНЕМАТИКУ
Кинематикой называется раздел механики, в котором изучаются движения материальных тел без учета их масс и действующих на них сил, то есть с чисто геометрической точки зрения.
Под движением в механике понимают изменение положения данного тела в пространстве по отношению к некоторой координатной системе, которую называют системой отсчета.
Таким образом, понятие движения является относительным. Тело, находящееся в покое относительно одной системы отсчета может совершать движение относительно другой системы отсчета.
Пространство в классической механике считается однородным, изотропным и евклидовым, а время является абсолютным, то есть протекающим одинаково во всех системах отсчета.
Для описания течения времени в механике используют независимую переменную − время. При этом все другие переменные величины рассматривают как функции времени. Отсчет времени ведут от некоторого начального момента = 0.
Основной задачей кинематики является изучение способов задания движения тел. Движение тела считается заданным, если для любого момента времени можно математически указать положение любой точки тела по отношению к данной системе отсчета.
Для описания движения кинематика кинематика использует кинематические характеристики, такие как скорости или ускорения, и устанавливает связывающие их математические зависимости.
76
Основными разделами кинематики являются:
кинематика точки,
кинематика твердого тела,
сложное движение точки,
сложное движение твердого тела.
1.2.СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
В кинематике используют три способа задания движения точки: векторный, координатный и естественный.
Векторный способ задания движения точки
Положение движущейся точки М по отношению к системе отсчета Оxyz можно задать радиус-вектором этой точки , который считается векторной функцией времени:
= ( ) |
(1.1) |
z 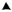
|
|
|
M |
|
|
|
|
|
r |
траектория |
|
|
|
z |
|||
|
|
|
|
||
k |
|
|
|
|
|
O |
|
j |
|
|
y |
|
|
|
|||
|
|
|
|
||
i |
|
|
|
x |
|
|
|
|
|
||
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1 |
|
|
Уравнение (1.1) представляет собой уравнение движения точки в векторной форме. Линия, которую описывает точка в своем движении,
называется ее траекторией точки.
Траектории движения точек можно разделить на прямолинейные и криволинейные.
Конец радиус-вектора указывает на точку М и в процессе движения всегда заканчивается на её траектории.
Таким образом, траектория точки является годографом вектора .
77
Координатный способ задания движения точки
Положение точки в данной системе отсчета можно определить, задав ее координаты в виде функций времени. В декартовой системе координат это будут функции
= ( ), { = ( ), (1.2)
= ( ).
Эти уравнения можно рассматривать как уравнения траектории точки, заданные в параметрической форме. Время в данном случае будет являться параметром. Чтобы получить уравнение траектории в явной форме надо из уравнений (1.2) исключить время.
Связь между векторным и координатным способами задания движения точки дается формулой
|
|
|
|
(1.3) |
|
|
|
= + + , |
|
где , |
, |
|
– единичные вектора (орты) декартовой системы координат. |
|
|
||||
Естественный способ задания движения точки
Этот способ применяется когда заранее известна траектория точки.
A |
O |
|
M |
|
траектория |
|
|
|
|
|
|
|
|
s |
|
B
Рис. 1.2
Чтобы задать движение некоторой точки М естественным способом, следует указать:
1.траекторию точки (кривая АВ на рис. 1.2);
2.начальную точку на ней (точка О на рис. 1.2);
3.положительное и отрицательное направление отсчета по траектории;
4.уравнение движения точки по траектории:
= ( ), |
(1.4) |
в котором s есть дуговая координата, то есть длина дуги по траектории между точками О и М, взятая со знаком «плюс» или «минус» в зависимости от того в какой части траектории находится точка.
Дуговая координата определяет положение точки на траектории движения, а не пройденный ею путь.
1.3.СКОРОСТЬ ТОЧКИ
Определение скорости при векторном способе задания движения

78
Скоростью точки называется кинематическая характеристика движения, равная производной по времени от радиус-вектора этой точки:
= |
|
= ̇ |
(1.5) |
|
В дальнейшем точкой сверху будем обозначать производную по времени.
|
– |
Система координат при этом считается неподвижной, а орты , , |
|
постоянными, как по величине, так и по направлению. |
|
Скорость точки – величина векторная, ее направление показывает куда в данный момент движется тело, а ее модуль – быстроту изменения положения точки. Размерность модуля скорости: [ ] = м⁄с.
Определение скорости при координатном способе задания движения
Выразим вектор скорости через его проекции на координатные оси:
, (*)
= + +
По определению
= |
|
= ̇ |
|
|
|||
|
|
|
|||||
|
|
|
|
|
|||
Возьмем производную от радиус-вектора |
по времени: |
||||||
= + + |
|||||||
|
|
|
|
|
|
|
|
= |
|
= |
( + + ) = ̇ + ̇ + ̇ |
(**) |
|||
Сравнивая формулы (*) и (**) получим, что |
|
||||||
|
= ̇ |
|
|
|
|||
|
|
|
|
|
|
|
|
{ = ̇ |
|
|
(1.6) |
||||
= ̇,
где , , – проекции вектора скорости на координатные оси.
Обычным образом находятся модуль вектора скорости:
= √ 2 + 2 + 2
и его направляющие косинусы:
= ( , ) = ⁄ { = ( , ) = ⁄.
= ( , ) = ⁄
Определение скорости при естественном способе задания движения
При естественном способе задания движения точки известна ее траектория и уравнение движения = ( ). Каждому значению дуговой координаты соответствует свой радиус-вектор , который в этом случае можно рассматривать как сложную функцию:
= (( )).
