
9391
.pdfЛекция 44. Линейные дифференциальные уравнения второго порядка
Ранее мы рассмотрели несколько типов дифференциальных уравнений второго порядка, которые путем соответствующей замены переменной приводились к дифференциальным уравнениям первого порядка. Теперь мы перейдём к изучению важного класса линейных дифференциальных уравнений второго порядка, в которые неизвестная функция и ее производные входят линейно, т.е. имеющих вид
a0 (x) y′′ + a1 (x) y′ + a2 (x) y = f (x) , |
(44.1) |
где функции ai (x) , i =1,2,3 называют коэффициентами этого уравнения. Не умаляя общности, будем считать, что a0 (x) = 1, т.к. к такому виду
можно привести уравнение (44.1) после деления на a0 (x) ¹ 0 . Если |
правая |
часть этого уравнения равна нулю |
|
y′′ + a1 (x) y′ + a2 (x) y = 0 , |
(44.2) |
то такое уравнение называется однородным, в противном случае оно называется неоднородным.
Будем предполагать, что функции a1 (x), a2 (x) и f (x) непрерывны в интервале (a,b) . Записав уравнение следующим образом
y′′ = -a1 (x) y′ - a2 (x) y + f (x) ,
замечаем, что оно является частным случаем уравнения
y′′ = F (x, y, y′) = -a1 (x) y′ - a2 (x) y + f (x) .
Для существования и единственности решения задачи Коши требуется, чтобы функции F (x, y, y′) , Fy′(x, y, y′) и Fy′′ ( x, y, y′) были непрерывными. В данном случае
Fy′(x, y, y′) = −a2 (x) , Fy′′ (x, y, y′) = −a1 (x)
и, следовательно, условия теоремы Коши выполнены. Поэтому при любых начальных условиях
′ |
, x0 |
Î(a,b) |
(44.3) |
y(x0 ) = y0 , y (x0 ) = y1 |
уравнение (44.2) имеет единственное решение.
31

44.1. Линейный осциллятор. Уравнение вида (44.1) служит математической моделью разнообразных колебательных физических процессов. Например, рассмотрим движение груза массы m , подвешенного на пружине, массой которой пренебрегаем (см. рис. 44.1).
l
O

 x
x
Рис. 44.1
Предполагаем, что взаимодействие груза и пружины описывается законом Гука (сила пропорциональна удлинению). Вес груза mg ,
вызвавший удлинение l пружины, уравновешивается силой упругости, т.е. k l = mg . Введём систему координат, приняв за начало точку O –
положение равновесия груза на пружине. Выведем груз из положения
равновесия и попытаемся определить |
его положение в любой момент |
времени, т.е. будем искать координату |
x как функцию времени x = x(t) . |
Предположим также, что среда, в которой движется груз, оказывает сопротивление движению, пропорциональное (с коэффициентом пропорциональности h ) скорости движения. Применяя второй закон Ньютона к движущейся массе, получим
&& |
& |
|
|
mx |
= −hx − k ( l + x) + mg , |
||
откуда следует уравнение вида (44.2) mx + hx + kx = 0 . |
|||
|
&& |
& |
|
Другой пример относится к электрическому контуру с конденсатором |
|||
ёмкости C , самоиндукцией L и сопротивлением |
R (см. рис. 44.2). Пусть |
||
q – заряд конденсатора и, следовательно, |
I = q – |
сила тока в контуре. На |
|
|
|
& |
|
обкладках конденсатора возникает напряжение |
q / C , в самоиндукции – |
||
ЭДС, равная −L dI / dt , а падение напряжения на сопротивлении равно
−RI . В силу закона Кирхгофа получим линейное однородное дифференциальное уравнение второго порядка
q&& + R q& + 1 q = 0 , L LC
32
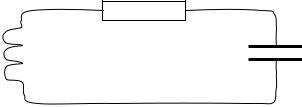
описывающее изменение заряда в этом контуре.
q
L R
C
Рис. 44.2
Рассмотренные в этом пункте математические модели, сводящиеся к линейному дифференциальному уравнению второго порядка с постоянными коэффициентами, называют линейным осциллятором.
44.2. Структура общего решения дифференциального уравнения второго порядка. Прежде, чем находить решения, отметим важные
свойства однородного уравнения (44.2). |
Пусть y1(x) и y2 (x) – |
два каких- |
либо непропорциональных друг другу |
решения этого уравнения, т.е. |
|
y2 (x) ¹ ly1 (x) . Тогда линейная комбинация этих функций |
|
|
y(x) = C1 y1 (x) + C2 y2 (x) |
(44.4) |
|
также будет его решением. В этом можно убедиться непосредственной подстановкой
(C1 y1 + C2 y2 )′′ + a1 (x)(C1 y1 + C2 y2 )′ + a2 (x)(C1 y1 + C2 y2 ) = |
|
|||
′′ |
′ |
′′ |
′ |
|
= C1 ( y1 |
+ a1 (x) y1 |
+ a2 (x) y1 ) + C2 ( y2 |
+ a1 (x) y2 + a2 (x) y2 ) = 0 . |
|
Теперь возникает |
вопрос: «не исчерпывают» ли |
линейные |
||
комбинации двух линейно независимых решений дифференциального уравнения (44.2) множество всех решений этого уравнения? Ответ на этот вопрос утвердителен.
В самом деле, пусть y* (x) – некоторое решение, удовлетворяющее начальным условиям
′ |
(x0 ) = y1 . |
y* (x0 ) = y0 , y* |
Покажем, что при некоторых значениях C1 и C2 линейная комбинация (44.4) совпадает с y* (x) . Для этого в силу единственности решения задачи Коши требуется, чтобы при некоторых C1 и C2 совпадали начальные
33

условия этой линейной комбинации и выбранного решения, т.е. система линейных алгебраических уравнений
C y (x ) + C |
2 |
y |
(x ) = y |
0 |
|||
|
1 |
1 |
0 |
2 |
0 |
||
|
|
|
|
|
y |
′(x ) = y |
|
C y ′(x ) + C |
2 |
||||||
|
1 |
1 |
0 |
2 |
0 |
1 |
|
имела единственное решение. Убедимся, что определитель этой системы,
называемый определителем Вронского
y1(x0 ) |
y2 (x0 ) |
, |
(44.5) |
|||
y ′(x ) |
y ′(x ) |
|||||
|
|
|||||
1 |
0 |
2 |
0 |
|
|
|
отличен от нуля.
Действительно, если предположить от противного, что этот определитель равен нулю, то соответствующая система однородных уравнений
C y (x ) + C |
2 |
y |
(x ) = 0 |
|||
|
1 |
1 |
0 |
2 |
0 |
|
|
|
|
(x ) + C |
|
|
(44.6) |
C y ′ |
2 |
y ′(x ) = 0 |
||||
|
1 |
1 |
0 |
2 |
0 |
|
имеет ненулевое решение (C1* ,C2* ) . Образуем функцию y( x) = C1* y1 ( x) + C2* y2 ( x) ,
которая также является решением дифференциального уравнения (44.2). Согласно (44.6) эта функция удовлетворяет нулевым начальным условиям. В силу теоремы единственности решения задачи Коши отсюда будет следовать, что она тождественно равна нулю, т.е.
|
C * y ( x) + C |
* y |
2 |
( x) ≡ 0 . |
|
||
|
1 |
1 |
2 |
|
|
|
|
Это значит, |
что функции |
y1(x) и |
y2 (x) линейно зависимы, |
т.е. |
|||
y2 (x) = λ y1 (x) . |
Мы получили |
|
противоречие, которое означает, |
что |
|||
определитель Вронского не равен нулю. Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка представляет собой линейную комбинацию любых двух его непропорциональных (линейно независимых) решений.
Перейдем теперь к неоднородному уравнению
y′′ + a1 (x) y′ + a2 (x) y = f (x) . |
(44.7) |
34 |
|

Пусть y(x) – какое-нибудь его решение. Покажем, что общее решение уравнения (44.7) имеет вид
y(x) = C1 y1 (x) + C2 y2 (x) + |
|
|
(x) , |
|
(44.8) |
|||||||
y |
|
|||||||||||
где y1(x) и y2 (x) – два |
каких-либо линейно |
|
независимых решения |
|||||||||
соответствующего однородного уравнения. В самом деле, |
||||||||||||
|
|
′′ |
|
|
|
|
|
′ |
|
|
|
|
|
|
+ a1 (C1 y1 + C2 y2 |
|
|
|
|
(C1 y1 + C2 y2 + y ) = |
|||||
(C1 y1 + C2 y2 + y ) |
+ y ) + a2 |
|||||||||||
|
′′ |
′ |
|
|
′′ |
′ |
|
+ a2 y2 ) + |
||||
= C1 ( y1 + a1 y1 + a2 y1 ) + C2 |
( y2 |
+ a1 y2 |
||||||||||
+( y′′ + a1 y′ + a2 y ) = f (x) ,
т.е. функция (44.8) будет решением уравнения (44.7) при любых значениях C1 и C2 . Очевидно, что для произвольного решения неоднородного
уравнения с заданными начальными условиями, решая линейную систему алгебраических уравнений, можно найти значения C1 и C2 , при которых
выбранное решение будет совпадать с функцией (44.8). Таким образом, общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
35
Лекция 45. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Особенно просто находятся решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
y′′ + a1 y′ + a2 y = 0 . |
(45.1) |
Будем искать решение этого уравнения в виде |
y = eλx . |
Вычисляя |
|||||||
производные и |
подставляя |
в (45.1), |
получим |
eλx (λ2 + a λ + a |
2 |
) = 0 . |
|||
|
y = eλx будет |
|
|
|
|
|
1 |
|
|
Следовательно, |
решением, |
если λ – |
корень |
квадратного |
|||||
уравнения |
|
|
|
|
|
|
|
|
|
|
λ2 + a λ + a |
2 |
= 0 , |
|
(45.2) |
||||
|
|
1 |
|
|
|
|
|
|
|
которое называют характеристическим уравнением соответствующего дифференциального уравнения.
Возможны следующие варианты. Если уравнение (45.2) имеет два
различных действительных корня λ |
и λ |
2 |
, то функции y = eλ 1x и y |
2 |
= eλ 2 x |
– |
1 |
|
1 |
|
|
непропорциональные решения уравнения (45.1) (их отношение, очевидно, не равно постоянной величине). В этом случае общее решение уравнения (45.1) имеет вид
y= C1eλ1x + C2eλ 2 x .
Вкачестве иллюстрации рассмотрим движение груза на пружинке. Напомним, что отклонение y(t) груза массы m от положения равновесия
под действием внешней силы f1 (t) приводит к уравнению
my′′ + hy′ + ky = f1 (t) ,
где второй член уравнения характеризует силу сопротивления среды, а третий «отвечает» за упругую силу пружины. По смыслу задачи коэффициенты h и k положительны. Введя очевидные обозначения, перепишем это уравнение следующим образом
y′′ + a1 y′ + a2 y = f (t) . |
|
|
|||
Пусть начальные условия: |
y(0) = y0 , |
′ |
= y1 |
, |
что соответствует |
y (0) |
|||||
заданию в начальный момент t0 = 0 положения груза и его начальной скорости. Рассмотрим сначала однородное уравнение
y′′ + a1 y′ + a2 y = 0 . |
(45.3) |
36 |
|
Это означает, что внешняя сила отсутствует. |
Корни характеристического |
|||||||||||||||||||||
уравнения определяются формулой |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
λ |
|
= − |
a |
± |
a2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
1 |
1 − a |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
||
|
|
|
/ 4 − a |
|
|
> 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть |
a2 |
2 |
|
т.е. корни |
действительные |
и |
различные. |
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положение груза в момент времени |
t |
определяется формулой |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y(t) = C*eλ 1t + C*eλ 2 t , |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
где конкретные |
значения постоянных |
C * , |
C* |
находим |
с |
помощью |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
начальных условий. Поскольку корни характеристического уравнения |
||||||||||||||||||||||
отрицательны, то с ростом |
|
|
t |
отклонение |
груза |
стремится |
к нулю. |
|||||||||||||||
Условие |
a2 |
/ 4 − a |
2 |
> 0 |
|
означает, |
что сила сопротивления среды |
больше |
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы упругости пружины. Пружина «слабая», а среда вязкая. |
|
|
||||||||||||||||||||
Рассмотрим конкретный пример |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
y |
′′ |
+ 7 y |
′ |
+ 6 y = 0, |
y(0) = 1, |
|
′ |
= 1. |
|
|
|
||||||
|
|
|
|
|
|
|
|
y (0) |
|
|
|
|||||||||||
Начальные условия означают, что пружину растянули и груз «толкнули» в |
||||||||||||||||||||||
том же направлении. |
График полученного решения |
y(t) = 1.4e−t − 0.4e−6t |
||||||||||||||||||||
приведён на рис. 45.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
y"+2y'+y=0 |
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y(0)=1,y'(0)=1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t)=(1+2t)exp(-t) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
y"+7y'+6y=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0.2 |
y(0)=1,y'(0)=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
y(t)=1.4exp(-t)-0.4exp(-6t) |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
0.5 |
|
|
1 |
|
1.5 |
|
2 |
2.5 |
3 |
3.5 |
t |
||||||
|
|
0 |
|
|
|
|
|
|
4 |
|||||||||||||
Рис. 45.1
Рассмотрим теперь случай, когда характеристическое уравнение
(45.2) имеет два одинаковых действительных корня |
λ = λ |
2 |
= − |
a1 |
(в таком |
|
|||||
|
1 |
2 |
|
||
|
|
|
|
||
37 |
|
|
|
|
|

случае говорят, что λ1 – корень кратности два). Из предыдущего следует, что функция y1 = eλ 1x будет решением дифференциального уравнения (45.1). Убедимся непосредственной подстановкой, что функция y2 = xeλ 1x также будет решением этого уравнения
(xy1 )′′ + a1 (xy1 )′ + a2 (xy1 ) = ( y1 + xy1′)′ + a1 ( y1 + xy1′) + a2 (xy1 ) = = x( y1′′ + a1 y1′ + a2 y1 ) + 2 y1′ + a1 y1 = 0 + (2λ1 + a1 )eλ1x = 0 .
Так как функции y1 = eλ 1x и y2 = xeλ 1x непропорциональны, то в этом случае общее решение уравнения (45.1) имеет вид
y= C1eλ 1x + C2 xeλ 1x = eλ 1x (C1 + C2 x) .
Вмодели движения груза на пружинке рассматриваемому случаю соответствует равенство a12 / 4 − a2 = 0 , когда корни характеристического
уравнения равны λ 1,2= −a1 / 2 . В физическом плане это означает, что сила сопротивления и сила упругости пружины «уравновешены» в смысле
указанного равенства. |
|
|
Тогда положение груза |
в момент времени t |
|||||||
определяется формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) = (C* + C |
− |
a1 |
|
t |
|
|
|
|
|
|
|
*t)e 2 . |
|
|||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
При малых значениях |
|
|
t основную «роль» |
играет первый множитель, |
|||||||
линейный относительно |
t , |
а затем |
с |
увеличением |
t груз будет |
||||||
стремиться к положению равновесия. Для конкретного примера |
|||||||||||
y |
′′ |
+ 2 y |
′ |
+ y = 0, y(0) |
= 1, |
|
|
′ |
|
||
|
|
|
y (0) = 1 |
|
|||||||
график решения y(t) = (1 + 2t)e− t также приведён на рис. 45.1. Сначала
груз движется под действием начального «толчка», а потом стремится к положению равновесия.
Остался последний |
случай – уравнение |
(45.2) |
имеет |
комплексные |
|||||||
|
|
|
α = −a / 2 , β = |
|
|
|
и i = |
|
|
. В этом |
|
корни λ |
|
= α ± βi , где |
a − a 2 |
|
|
|
|
||||
1,2 |
/ 4 |
|
|
−1 |
|||||||
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
случае дифференциальное уравнение будет иметь решением комплекснозначные функции вида e(α ±β i ) x . Выделим из них вещественные решения.
Применяя знаменитую формулу Эйлера
e(α±βi ) x = eαx (cosβx ± i sin βx) ,
38

можно убедиться, что в этом случае действительная и мнимая части этой
функции |
y = eαx |
cosβx |
и |
y |
2 |
= eαx sin βx |
образуют |
пару |
|
1 |
|
|
|
|
|
|
|
непропорциональных |
вещественных |
решений уравнения (45.1), |
а его |
|||||
общее решение имеет вид |
|
|
|
|
|
|
||
y= eαx (C1 cosβx + C2 sin βx) .
Вмодели движения груза на пружине этот случай характеризуется
неравенством a12 / 4 − a2 < 0 , физический смысл которого состоит в том,
что упругая сила пружины превосходит силу сопротивления среды. Обозначим, для краткости, корни характеристического уравнения
l 1,2 |
= a ± b × i, a = - |
a1 |
, |
b2 = - ( |
a12 |
- a2 ) . |
|
|
|||||
|
2 |
|
4 |
|
||
Вещественное решение уравнения, как мы показали ранее, имеет вид
y(t) = e α t (C1 cosβ t + C2 sin β t) .
Из школьного курса физики известно, что сумма двух гармонических колебаний с одинаковой частотой снова гармоническое колебание с той же частотой. Действительно,
|
|
|
|
С1 |
|
|
|
С2 |
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||
C1 cosβt + C2 sin βt = С1 |
|
|
|
|
|
cosβt + |
|
|
|
sin βt |
= |
||||
+ С2 |
С2 |
+ С2 |
|
С2 |
+ С2 |
|
|
||||||||
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
= 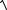
 С12 + С22 (sinγ0 cosβ t + cos γ0 sin β t ) =
С12 + С22 (sinγ0 cosβ t + cos γ0 sin β t ) = 
 С12 + С22 sin(β t + γ0 ) .
С12 + С22 sin(β t + γ0 ) .
Таким образом, груз будет совершать затухающие колебания с частотой β по закону, описываемому функцией
|
|
|
|
− |
a1 |
t |
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
||||
y(t) = C2 |
+ C2 |
e |
|
2 sin(βt + γ |
), |
tgγ |
0 |
= |
. |
|||
|
|
|||||||||||
1 |
2 |
|
0 |
|
|
|
C2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Это так называемые собственные колебания изучаемой физической системы. Напомним, что рассмотренные модели вида (45.1), которые описывают движение груза на пружине или изменения заряда в электрическом контуре, мы называли линейным осциллятором.
Рассмотрим конкретный пример
y |
′′ |
+ 0, 2 y |
′ |
+ 1,01y = 0, |
′ |
= 1. |
|
|
y(0) = 0, y (0) |
||||
|
|
|
|
39 |
|
|
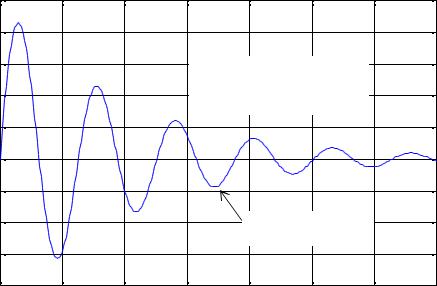
Так как корни характеристического уравнения комплексные λ 1,2 |
= −0,1 ± i , |
||||
то решение имеет вид |
y(t) = e |
−0,1t (C cos t + C |
2 |
sin t) . Найдя |
значения |
|
|
1 |
|
|
|
постоянных, получим y(t) = e−0,1t sin t . График этого решения приведён на рис. 45.2.
1 |
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
0.6 |
|
|
y′′ + 0, 2 y′ + 1,01y = 0 |
|
|||
|
|
|
|
||||
0.4 |
|
|
y(0) |
= 0, |
′ |
= 1 |
|
|
|
|
y (0) |
|
|||
0.2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
|
-0.4 |
|
|
|
y(t) = e−0,1t sin t |
|
||
|
|
|
|
|
|||
-0.6 |
|
|
|
|
|
|
|
-0.8 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
0 |
|||||||
Рис. 45.2
В идеальном случае, когда сопротивление среды отсутствует, уравнение y′′ + a2 y = 0 удобно записать в виде y′′ + ω2 y = 0 . Его решение
y(t) = C1 cos ωt + C2 sin ωt = Asin(ωt + γ0 ) |
(45.4) |
представляет собой гармонические незатухающие колебания с частотой ω .
Лекция 46. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
40
