9389

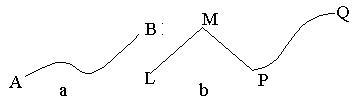
Рис. 54.2

Теорема. Если непрерывная кривая AB может быть разбита на конечное число гладких кусков и в некоторой окрестности этой кривой функция f (x, y, z) непрерывна, то для нее существует криволинейный интеграл (54.2).

Наряду со свойствами, которые имеют все рассмотренные ранее интегралы (постоянн ое число можно выносить за знак ин теграла; интеграл от суммы или раз ности двух функций равен сум ме или разности интегралов от этих ф ункций), отметим еще ряд свойст в криволинейного интеграла 1-го рода.

а) Криволинейный интеграл 1-го рода не зависит от направления

начале параграфа. Однако анализ конструкции (54.2) показывает, что при

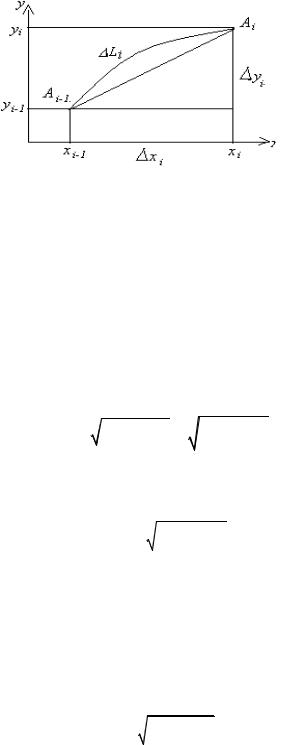
получим формулу для вычисления длины дуги AB .

Рис. 54.3

Нетрудно видеть, что под знаком предела стоит интегральная сумма для функции 1 ′ на отрезке (a,b), и потому последний

предел равен определенному интегралу от этой функции на этом отрезке. Таким образом,

b

L = ∫ dl = ∫ 1+ y′ 2 (x)dx

AB a

Пусть теперь f (x, y) – произвольная непрерывная функция, определенная в точках близких к кривой AB . Так как, согласно определению, точка Pi

на отрезке кривой Ai−1Ai может выбираться произвольным образом, то

104

определенному интегралу от этой функции на данном отрезке. В результате мы приходим к формуле

Рис. 54.4

Решение. Так как y′ = −2x , то по формуле (54.3) искомая масса будет равна

105

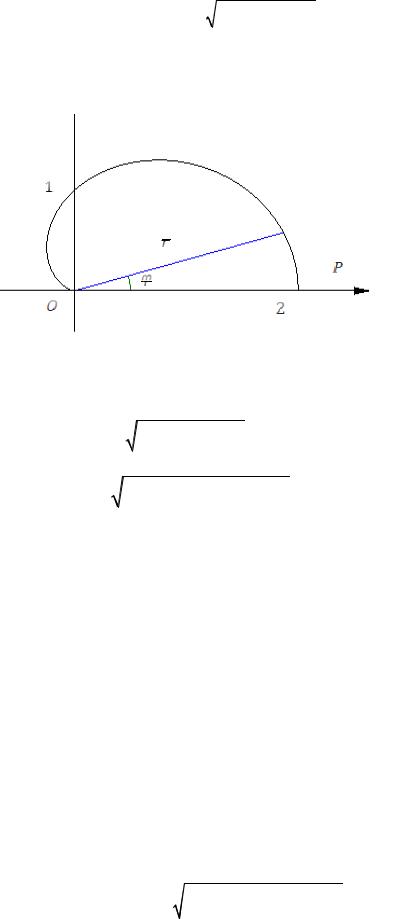
Пример. Найти массу половины кардиоиды r = (1+ cosϕ), 0 ≤ ϕ ≤ π,

если плотность ρ = r в каждой её точке.

Рис. 54.5

Пользуемся формулами (54.3) и (54.10):

Общий пространственный случай. Если кривая AB расположена в пространстве, то, как правило, она задается параметрическими уравнениями

x = x(t); y = y(t); z = z(t) α≤ t ≤ β,

причем параметру t = α соответствует точка A, а параметру t = β соответствует точка B . Предполагая, что производные x′(t), y′(t), z′(t) непрерывны при α ≤ t ≤ β, а функция f(x,y,z) непрерывна в некоторой

области D, окружающей кривую AB, и, проводя рассуждения, подобные приведенным для плоского случая, придем к следующей формуле:

54.3. Некоторы е приложения криволинейного интеграла 1-ого

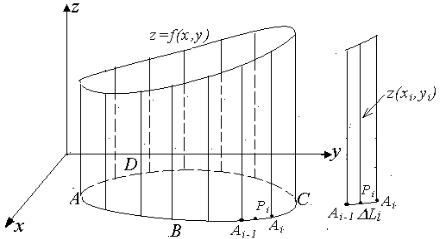
рода. Определение площади цилиндрической поверхности. На рис. 54.6

изображено ограждение переменной высоты некотор ой горизонтально расположенной терр итории, ограниченной кривой L. Вопрос о расходе краски, необходимой для окраски этого огражде ния, сведется к нахождению его пло щади. Если ввести систему координат так, чтобы территория находилась в плоскости XOY, то можно считать, что данное ограждение представ ляет собой часть цилиндрической поверхности с направляющей L и образующей, параллельной оси OZ, причем высота ограждения задается функцией z = f ( x, y ) , определенно й в каждой точке

кривой L (рис.54.6). Если рассмотреть часть поверхности на небольшом

участке кривой Ai−1Ai , то можно считать, что высота этой части постоянна и

Рис. 54. 6

Суммируя по всем участкам и переходя к пределу в получающейся интегральной сумме, мы придем к тому, что площадь всей боковой

(Канаты, на которых подвешен мост через пролив Босфор, соединяющий Черное и Средизем ные моря, можно рассматривать в качестве примера такого объекта. В качестве математической модели канатов можно

108

рассматривать их оссевые линии с постоянной линейной плотностью, равной массе тонкого слоя поперечного сечения). В такомм случае основные механические характе ристики подобных объектов могут быть вычислены с помощью криволинейного интеграла 1-ого рода.

а) Масса материальной кривой. Как мы уже знаем, масса М такой кривой может быть в ычислена по формуле (54.3).

б) Моменты инеерции I x, I y, I z относительно осей OX , OY , OZ . Перечисленные моменты вычисляются по следующим формулам

мелкие участки и считаем, что вся масса отрезка кривой (приблизительно равная ρ(ξi ,ηi , νi ) Li ) сосредоточена в некоторой ее точке P(ξi , ηi , νi ).

Момент инерции этой материальной точки относительнно, например, оси OX, будет равен ее массе, умноженной на квадрат расстояния от оси, т.е. ρ(ξi ,ηi ,νi ) Li (ηi2 +νi2 ). Суммируя по всем отрезкам кривой и переходя к

пределу, получаем искомые выражения.

в) Kоординаты центра тяжести. Координаты центра тяжести C(xc , yc , zc ) материальной пространственной кривой могут быть высчитаны

по формулам:

имеем дело с плоской кривой и потому в соответствую щих формулах мы должны опустить переменную z. Очевидно, что масса M равна длине полуокружности, умноженной на ρ , т.е. M = πρR .

Рис. 54. 7

109

Для нахождения моментов инерции Ix и Iy сначала запишем уравнение полуокружности в параметрическом виде

110

Лекция 55. Криволинейные интегралы 2-г о рода (по координатам)

Вданной лекции мы рассмотрим еще одн у интегральную

конструкцию, котор ая, как и все рассмотренные ра нее, изначально возникла при стремлении решить некоторую прикладную задачу (именно в физике), а потом оказалась применимой при решении других теоретических и пр икладных задач. Речь идет о криволинейных интегралах 2-го рода.

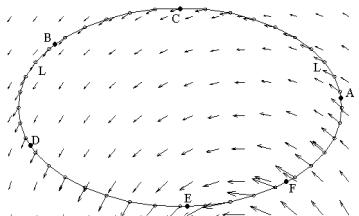
55.1. Определение и обозначения. Физическая задача, в которой подобная конструкц ия возникает, формулируется след ующим образом. Пусть в некоторой об ласти D пространства определено силовое поле, т.е. на материальную точку единичной массы, помещенную вR область D, действует зависящая от ее местонахождения вектор-сила F . И пусть в этой области материальная точка перемещается по кривой L из положения A в положение B. Требуется определить работу W сил данного поля при таком перемещении.

Рис. 55.1

На рисунке 55 .1 изображено плоское поле сил. Ясно, что при перемещении точки по кривой L по участку кривой ACB силы поля оказывают положительное воздействие, т.е. совершают положительную работу, а при движении по участку кривой DEF они оказывают отрицательное воздей ствие, т.е. совершают отрицательную работу. Точно также при спуске с горы мы ощущаем положительное воздействие силы тяжести, а при подъеме в гору нам приходится преодолевать отрицательное воздействие этой силы.

Если в пространстве введена декартова система к оординат, то сила, действующая в точке может задаваться посредством ее

R R R

разложения по едини чным векторам i , j,k

111