Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

9368

.pdf

Скачиваний:

Добавлен:

25.11.2023

Размер:

2.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

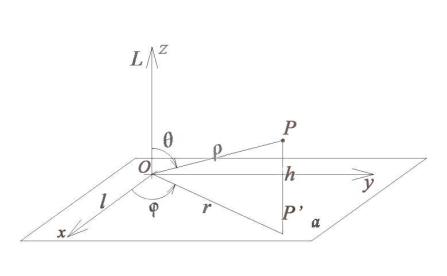
Лекция 53. Тройной интеграл в сферических координатах. Приложения к механике

53.1. Вычисление тройного интеграла в сферических координатах.

Чтобы ввести сферические координаты в трёхмерном пространстве,

рассмотрим снова плоскость α и перпендикулярную				ей ось	L . На
плоскости α введём ось l . Тогда сферические координаты (ρ, ϕ, θ)					точки
P будут представлять собой соответственно её расстояние ρ от начала
координат (длина радиус– вектора точки	P ),	угол	ϕ между проекцией
OP ′ радиус-вектора точки P на плоскость α и осью l , а				также угол θ
между радиус-вектором OP и осью	L	(рис.	53.1).	Координатная

поверхность ρ = const является сферой, что объясняет название координат. Для описания всех точек в пространстве достаточно следующих

промежутков изменения координат: 0 ≤ ρ < ∞, 0 ≤ θ ≤ π, 0 ≤ ϕ < 2π . Введём декартову систему координат, совместив ось Ox с осью l , а

плоскость xOу декартовой системы – с плоскостью α (рис. 53.1). Декартовы координаты точки P обозначим (x, y, z) , тогда координаты её проекции P′ на плоскость xOу приобретут значения (x, y, 0) . Поскольку расстояние r = OP′ и угол ϕ являются полярными координатами точки

P′ , то x = r cos ϕ , y = r sin ϕ.

Рис. 53.1

Учитывая, что OP′ = ρsinθ и z = ρcosθ, получим связь сферических и декартовых координат в виде

	x = ρsin θcos ϕ

	y = ρsin θsin ϕ	(53.1)
		(53.1)

	z = ρcosθ

Пусть для примера поверхность задана в декартовых координатах уравнением

(x 2 + y 2 + z 2 )2 = a 2 (x 2 + y 2 ).

По такому уравнению представить вид поверхности весьма непросто. Перейдём к сферическим координатам, пользуясь соотношениями (53.1)

	ρ2 sin2	θcos2	ϕ+ ρ2 sin2 θsin2 ϕ+ ρ2 cos2 θ 2	=

= a2 (ρ2 sin2 θcos2 ϕ+ρ2 sin2 θsin2 ϕ) .

После очевидных преобразований уравнение упрощается

ρ4 (sin2 θ + cos2 θ)2 = a2ρ2 sin2 θ ,

что дает ρ2 = a2 sin2 θ или, окончательно, ρ = a sin θ .

Теперь можно представить вид поверхности. Во-первых, ясно, что она имеет одинаковые сечения плоскостями ϕ = const . Во-вторых, можно определить вид этих сечений. Для этого перейдём в плоскости yOz к

декартовым координатам по формулам, которые получаются из (53.1), если

ϕ = π2

z = ρcosθy = ρsin θ .

Уравнение сечения рассмотрим в виде ρ2 = aρsinθ, что дает в координатах ( y, z) уравнение y2 +z2 =ay или после выделения полного квадрата

y − a2

+ z2 = a .2

Видим, что сечение это является окружностью радиуса a .

Пришли к тому, что исходная поверхность представляет собой тор, т.е. закрученную вокруг оси Oz окружность, закрепленную в начале координат (половина поверхности изображена на рисунке 53.2).

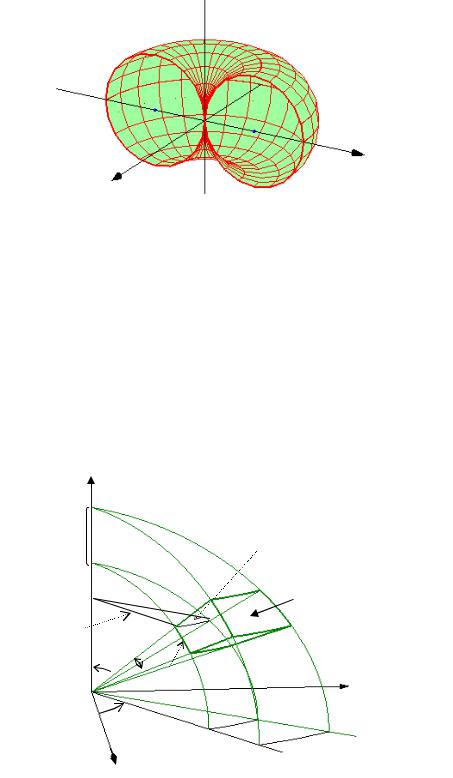
Рис.53.2

Чтобы найти элементы объёма в сферических координатах, построим поверхности семейств ρ = const (сферы), θ = const (конические поверхности с вершиной в начале координат) и ϕ = const (полуплоскости, проходящие через ось Oz ). Рассмотрим один из элементов Ωi ,

ограниченный сферами радиусов ρ	и ρ + dρ , конусами растворов θ и
θ + dθ , а также полуплоскостями,	проведёнными через ось Oz , следы

которых в плоскости xOу имеют полярные лучи ϕ и ϕ + d ϕ (рис. 53.3).

dρ

ρsinθdϕ

Ωi

ρsinθ

θdθ

ρdθ		y
ϕ	ρ
	ρ	dϕ
x		dϕ
x

Рис. 53.3

Представив подобласть Ωi как прямоугольный параллелепипед со сторонами dρ , ρdθ и ρsinθdϕ, получим элементарный объём в виде

dV = ρ2 sin θ dρdϕdθ. Поэтому формула перехода в тройном интеграле от декартовых координат к сферическим приобретает вид

∫∫∫ f (x, y,z)dxdydz =∫∫∫ f (ρsinθcosϕ,ρsinθsinϕ,ρcosθ)ρ2sinθdρdϕdθ .
Ω	Ω

Итак, при переходе в тройном интеграле от декартовых к сферическим координатам подынтегральная функция должна быть выражена через

переменные ρ , ϕ и θ по формулам (53.1), а также умножена на ρ2 sinθ. Сферические координаты используем для нахождения объёма тела

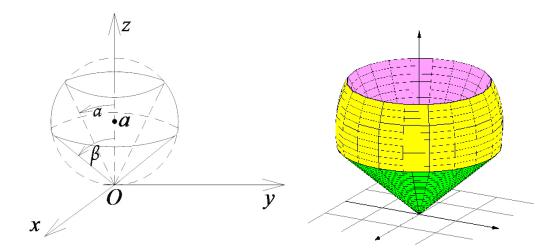
Ω , ограниченного сферой x2 + y2 + z2 = 2az и двумя коническими

поверхностями x2 + y2 = z2tg2α	и x2 + y2 = z2tg2β, если 0 < α < β < π
(рис. 53.4).	2
(рис. 53.4).

Рис. 53.4

Пользуясь формулами, связывающими декартовы и сферические координаты, запишем уравнение исходной сферы с центром в точке (0,0,a)

и радиуса a в виде

ρ2 sin2 θcos2 ϕ+ρ2 sin2 θsin2 ϕ+ρ2 cos2 θ = 2aρcosθ,

что дает после преобразований ρ = 2acosθ.

Теперь можно задать область Ω в сферических координатах условиями

0≤ρ≤2acosθ, 0≤ϕ≤ 2π, α≤θ≤β.

Тогда объем находится следующим образом:

	β	2π 2acosθ
V = ∫∫∫ρ2 sinθdϕdρdθ= ∫dθ ∫ dϕ			∫ ρ2 sinθdρ=
Ω	α	0	0

β	2π	8a3		θdϕ =	4πa3
= ∫dθ ∫ sinθ		8a3	3		4πa3	4	4	β) .
= ∫dθ ∫ sinθ		3	cos		3	(cos	α−cos	β) .
α	0

Заметим, что сферические и цилиндрические координаты являются ортогональными координатами (их координатные линии пересекаются под прямым углом). Иногда применяют и неортогональные координаты, но мы оставим это за рамками нашего рассмотрения.

53.2. Статические моменты, координаты центра тяжести, моменты инерции пространственных тел. Если пространственную область Ω рассматривать как материальное тело, то с помощью тройного интеграла можно находить для него координаты центра тяжести и моменты инерции относительно некоторой плоскости, точки или оси. Формулу нахождения массы пространственного тела как интеграла от объёмной плотности мы уже получили.

Пусть ограниченное материальное тело Ω в пространстве имеет объёмную плотность, заданную функцией γ = γ(x, y, z) . Для определения

координат центра тяжести плоских областей использовались статические моменты относительно осей координат. Для пространственной области

следует рассматривать	статические	моменты M yoz , M xoz ,M xoy
относительно соответствующих координатных плоскостей.
Будем рассуждать	так же, как	при нахождении массы

пространственного тела. Во-первых, разобьём тело Ω на n тел. В пределах каждого тела Ωi будем считать объёмную плотность постоянной и

равной её значению γ(xi , yi , zi ) в некоторой точке Pi (xi , yi , zi ) . Если далее считать, что вся масса Mi подобласти Ωi сосредоточена в точке Pi (xi , yi , zi ) , то можно рассматривать тело Ω как систему материальных точек. Тогда для статического момента относительно координатной

плоскости	yOz получим приближённое значение, выраженное через
объём V	части пространства, занимаемого телом Ω	i
i		i

Myoz ≈∑xi

i=1

Mi ≈∑xi γ(xi,yi,zi) Vi .

i=1

При диаметре разбиения, стремящемся к нулю, интегральные суммы перейдут в пределе в двойной интеграл

M yoz = ∫∫∫ xγ(x, y, z)dxdydz .

Аналогично получа ются статические				моменты				относительно других
координатных плоск остей.	С помощью этих						статических моментов
вычисляются координаты центра тяжести тела							Ω по формулам
x =	Myoz		y =	M			=	Mxoy
		,		xoz	,	z			.

c	M		c	M		c		M

При постоянной объёмной плотности эти формулы приобретают вид

xc =

∫∫∫xdxdydz,

yc =

∫∫∫ydxdydz,

zc =

∫∫∫zdxdydz .

Найдем для примера центр тяжести однородного поллушара радиуса R

с центром в начале координат

(рис. 53.5).

Из соображений симметрии

ясно, что две коордиинаты центра тяжести

xc и yc

равны 0 . Чтобы

вычислить zc , записываем соответствующую формулу

2πR3

∫∫∫

zc =

zdxdydz .

Рис. 53.5

Учитывая, что сечениие D полушара			плоскостью z =const представляет
	z
		(рис.	53.5) с площадьюю S(z) =π(R2 −z2 ) ,
собой круг радиуса	R2 −z2	(рис.	53.5) с площадьюю S(z) =π(R2 −z2 ) ,
получим

	R			R	R	− z2)dz = πR4 .
∫∫∫ zdxdydz =∫ zdz ∫∫ dxdy = ∫ zS(z)dz = ∫ zπ(R2
Ω	0	Dz		0	0	4

Окончательно найдем		zc =	3	×πR4	= 3 R .

		2πR3		4	8

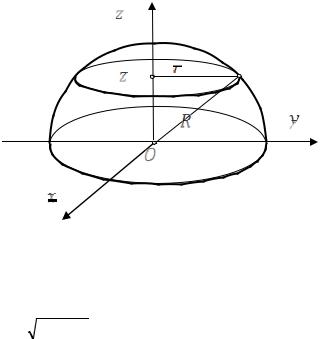
Моменты инерции относительно осей, точек и координатных плоскостей для пространственных тел определяются аналогично моментам инерции плоских фигур: интегрируется произведение плотности на квадрат расстояния до оси, точки или плоскости. Нужно учесть при этом,

				до оси Ox равно
что расстояние от произвольной точки			P(x, y, z)	до оси Ox равно		y2 + z2
					, до плоскости xOу
, до оси Oy равно	x2 + z2	, до оси Oz	равно	x2 + y2	, до плоскости xOу
равно z и так далее (рис. 53.6).

Рис. 53.6

Поэтому момент инерции относительно оси Ox записывается в виде

Ix = ∫∫∫( y2 + z2)γ(x, y,z)dxdydz ,

момент инерции относительно координатной плоскости xOу

Ixoy = ∫∫∫ z2γ(x, y,z)dxdydz ,

аналогично – для других осей координат и координатных плоскостей. Момент инерции относительно начала координат равен

I0 = Ixoy + Ixoz + I yoz .

Записанные формулы упрощаются в случае однородных пространственных тел с постоянной объёмной плотностью.

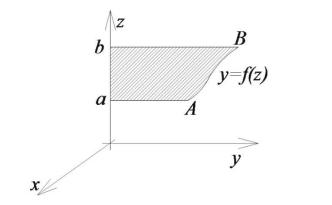
Найдем для примера момент инерции тела, полученного в результате вращения вокруг оси Oz криволинейной трапеции aABb (рис. 53.7) относительно его оси симметрии.

Рис. 53.7

Здесь	y = f (z) – неотрицательная и непрерывная			на	отрезке	a,b

функция. Считаем объёмную плотность постоянной					γ(x, y, z) ≡ γ		и
используем выписанную ранее формулу в виде
	I z = γ∫∫∫ ( x2 + y 2 )dxdydz .
	Ω
Вычисляем тройной интеграл
	b
	I z = γ∫ d z ∫∫ ( x 2		+ y 2 )d xd y ,
	a	D z
где D	– сечение исходного тела вращения плоскостью z = const , которое
z
представляет собой круг радиуса		y(z) .	Если D -	круг радиуса			R с

центром в начале координат, то, переходя к полярным координатам, можно найти

	2 π	R	2π r4		R
∫∫( x 2	+ y 2 )dxdy = ∫ d ϕ ∫(r 2 cos2 ϕ + r 2 sin 2 ϕ)rdr =				dϕ=	πR4
			∫	4
D	0	0			2 .
			0		0

Тогда для тела вращения вместо R достаточно подставить его выражение как функцию y(z)

I = γ	b		y 4 ( z )	d z =	πγ	b
		π					y 4 ( z )d z
	∫					∫		.
z		2		2

	a					a

Полученную формулу удобно использовать для вычиисления моментов инерции конкретных тел вращения. Например, для конуса радиуса R и высоты H с постоянной плотностью γ(x, y, z) ≡ γ (см. рис. 53.8) имеем

Рис. 53.8

π γ H

πγR 4

3 M R 2

I z

∫

d z =

H =

1 0

так как его масса
M = γ	πR 2 H	.
M = γ	3	.
	3

Раздел 10. Криволинейные интегралы

Лекция 54. Криволинейный интеграл 1-го рода (по длине дуги)

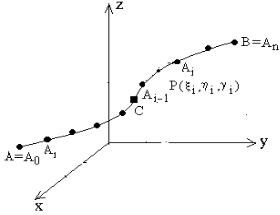
54.1. Определение. К понятию криволинейного интеграла 1-ого рода приводит вычислительная конструкция, возникающая, например, при попытке точного решения задачи об определении массы неоднородной материальной линии. Задача формулируется так. Пусть в каждой точке P(x, y, z) линии AB в пространстве определена плотность ρ( x, y , z )

(рис. 54.1). Требуется найти массу этой линии.

Рис. 54.1

Под плотностью	массы	вдоль		кривой		AB	в точке P0 (x0 , y0 , z0 )
понимается величина	ρ ( x , y , z		)	= lim	m , где		l – длина отрезка
	0 0	0	0	l → 0	l
					l
кривой, содержащего точку P0(x0, y0, z0) , а					m –	масса этого отрезка. Если

плотность в каждой точке линии одинакова и равна ρ0 , то масса

вычисляется по формуле

M =ρ0L, где

L – длина кривой от точки

A до

точки

B . Если же плотность вдоль линии изменяется,

то эта формула

неприменима.

Разовьем следующую идею приближенного вычисления массы этой

линии.

Разделим

линию

на

небольших

участков

точками

A = A , A, A , A ,...,A = B и будем считать,

что на участке

A A плотность

1 2

i−1 i

постоянная,

например,

такая,

как

некоторой

точке

P(ξi ,ηi , νi ) ,

принадлежащей, отрезку кривой Ai−1 Ai .

Тогда масса участка Mi может быть

приближенно вычислена по формуле

= ρ(ξ

,η , ν

)

l ,

где

есть

i i

длина участка линии от точки

до точки A. Масса всей линии может

i−1

быть приближенно вычислена по формуле

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.20232.59 Mб09363.pdf
#
25.11.20232.59 Mб09364.pdf
#
25.11.20232.59 Mб09365.pdf
#
25.11.20232.6 Mб09366.pdf
#
25.11.20232.6 Mб09367.pdf
#
25.11.20232.61 Mб09368.pdf
#
25.11.20232.61 Mб09369.pdf
#
21.11.2023163.81 Кб0937.pdf
#
25.11.20232.61 Mб09370.pdf
#
25.11.20232.61 Mб09371.pdf
#
25.11.20232.61 Mб09372.pdf