
9301
.pdf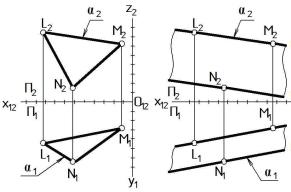
21
Так как пирамида наклонная, то все три координаты вершины S являются основными.
Замечание: ребра как призмы, так и пирамиды на этом этапе рекомендуется выполнить тонкими линиями, поскольку в дальнейшем их видимость будет уточняться.
Рассмотрим порядок построения двухкартинного комплексного чертежа плоскости. В работе плоскость однозначно определяется тремя точками, не лежащими на одной прямой L, M, N и задается ими на чертеже (Рис. 5). Заметим, что чертеж плоскости выполняется в тех же осях, что и многогранник.
В зависимости от геометрических условий, плоскость может быть задана:
∙ треугольником α ( LMN). В этом случае проекции следует обозначить отсеками треугольников, соединив соответствующие проекции точек отрезками прямых линий: α1 ( L1M1N1), α2 ( L2M2N2) (Рис. 5 а);
∙ двумя параллельными прямыми α (m // n), m L; M, n N. В
этом случае сначала необходимо построить проекции соответствующих фрагментов прямых m и n, затем обозначить отсеки, соединив соответствующие концы прямых волнистыми линиями обрыва: α1 (m1 // n1),
α2 (m2 // n2) (Рис. 5 б).
а |
б |
Рисунок 5
22
2. Определение собственной видимости ребер многогранника
Для определения видимости элементов чертежа используется метод конкурирующих точек. Напомним, что конкурирующими называются точки, лежащие на одной проецирующей прямой.
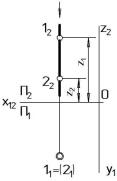
Например, на рис. 6 представлена пара конкурирующих точек 1 и 2, принадлежащих горизонтально-проецирующей прямой. Определим, какая из этих точек видима на горизонтальной плоскости проекций Ï1.
Рисунок 6
Вопрос о видимости этих точек на Ï1, где обе точки проецируются в одну, решается следующим образом: из двух совпадающих проекций конкурирующих точек, лежащих на одной горизонтально-проецирующей прямой видна та, высота (z) которой больше (или видна та точка, которая расположена дальше от Ï1 по ходу проецирования, показанного стрелкой). Посмотрим на Ï2 высота какой точки больше? Для этого сравним координаты z проекций 12 и 22. z1 > z2, то есть высота точки 1 больше. Следовательно, на плоскости Ï1 проекция 11 видима, невидимую точку (21) заключаем в скобки. Действительно по ходу проецирования первой будет получена проекция 21, затем 11, так как 12 расположена дальше от Ï1.
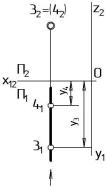
На рис. 7 представлена пара конкурирующих точек 3 и 4, принадлежащих фронтально-проецирующей прямой. Определим, какая из этих точек видима на фронтальной плоскости проекций Ï2.
23
Рисунок 7
Вопрос о видимости этих точек на Ï2 решается следующим образом:
из двух совпадающих проекций конкурирующих точек, лежащих на одной фронтально-проецирующей прямой видна та, глубина (y) которой больше
(или видна та точка, которая расположена дальше от Ï2 по ходу проецирования, показанного стрелкой).
Посмотрим на Ï1 глубина какой точки больше? Для этого сравним координаты y проекций 31 и 41. y3 > y4, то есть глубина точки 3 больше, следовательно, 32 видима, невидимую точку (42) заключаем в скобки. Действительно по ходу проецирования первой будет получена проекция 42, затем 32, так как 31 расположена дальше от Ï2.
Рассмотрим определение видимости ребер многогранника на примере четырехугольной пирамиды. Порядок определения видимости проекций следующий:
Этап 1. Определить видимость очерковых линий.
Очерковыми называются линии, по отношению к которым все точки изображаемого объекта расположены по одну сторону. Эти линии видны всегда.
Для пирамиды на Ï2 видима фронтальная очерковая замкнутая ломаная линия S2 B2 C2 D2 S2, на Ï1 - горизонтальная очерковая замкнутая ломаная линия S1 D1 C1 B1 S1 (Рис. 8).

24
Рисунок 8
Этап 2. Определить видимость ребер внутри очерка на горизонтальной плоскости проекций Ï1.
На Ï1 возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 1 [ÀÂ] и 2 [SC]. На Ï1 проекции этих точек 11 и 21 совпадают (Рис. 9).
Рисунок 9
Вопрос видимости для 11 и 21 решается на Ï2, где их проекции разнесены. На Ï2 проекция точки 12 расположена выше проекции 22 (координата z1 > z2), следовательно, точка 1 расположена в пространстве выше точки 2 и прикрывает ее собой.
Таким образом, на чертеже в плоскости Ï1 видна проекция точки 11 и проекция ребра, к которому она относится - [À1Â1]. Ребро обозначается основной линией. Невидимая на Ï1 проекция 21 принадлежит ребру [S1C1], следовательно это ребро невидимое и обозначается штриховой линией.
25
Внутри очерка остались ребра [À1D1], [S1A1], они видимые, поскольку имеют общую с видимым ребром [À1Â1] вершину A1.
Этап 3. Определить видимость ребер внутри очерка на фронтальной плоскости проекций Ï2.
На Ï2 возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 3 [SC] и 4 [ÀÂ]. На Ï2 проекции этих точек 32 и 42 совпадают (Рис. 10).
Рисунок 10
Вопрос их видимости решается на Ï1: глубина точки 31 больше, чем у
41 (координата y3 > y4), следовательно, точка 3 расположена в пространстве перед точкой 4 и прикрывает ее собой.
По видимости проекций точек определяется видимость соответствующих ребер на Ï2. Ребро [S2C2] видимое, ребро [À2Â2] и пересекающиеся с ним в вершине À2 ребра [À2D2], [S2A2] – невидимые.
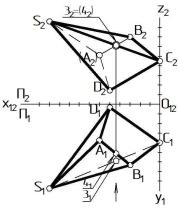
Рассмотрим особенности определения видимости ребер на примере треугольной пирамиды (Рис. 12).
Порядок определения видимости проекций аналогичный:
Этап 1. На Ï2 видима фронтальная очерковая S2 C2 À2 S2, на Ï1 - горизонтальная очерковая S1 C1 B1 S1 замкнутые ломаные линии.
Этап 2. Плоскость Ï1: внутри очерка нет скрещивающихся ребер, три пересекающиеся ребра [S1À1], [C1À1], [B1À1] будут иметь одинаковую видимость, определяемую видимостью общей вершины À1.

26
Рисунок 12
Вопрос видимости для À1 решается на Ï2. Проекция точки À1 расположена ниже всех вершин пирамиды (координата zÀ = min), следовательно, точка À расположена в пространстве ниже точек фигуры, следовательно, À1 - невидимая .
Этап 3. Плоскость Ï2: внутри очерка нет скрещивающихся ребер, три пересекающиеся ребра [S2Â2], [C2Â2], [À2B2], будут иметь одинаковую видимость, определяемую видимостью общей вершины B2. Вопрос видимости для B2 решается на Ï1. Проекция точки B2 имеет наибольшую глубину среди всех вершин пирамиды (координата yB = max), следовательно, точка B2 видимая.
Для призмы на рис. 13 видимость определяется в том же порядке.
Рисунок 13
27
Этап 1. На Ï2 видима фронтальная очерковая E2 E2’ F2’ G2’ G2 H2 E2, на Ï1 - горизонтальная очерковая E1 F1 G1 G1’ H1’ E1’ E1 замкнутые ломаные линии.
Этап 2. Плоскость Ï1. На Ï1 возьмем пару конкурирующих точек,
принадлежащих скрещивающимся ребрам пирамиды. Пусть 1 [E’G’] |
и |
2 [G’H’]. На Ï2 проекция точки 12 расположена выше проекции |
22 |
(координата z1 > z2), следовательно, точка 1 расположена в пространстве выше точки 2. Таким образом, на плоскости Ï1 видна проекция точки 11 и проекция ребра, к которому она относится - [E1’G1’]. Видимость остальных ребер понятна из чертежа.
Этап 3. Плоскость Ï2.На Ï2 возьмем пару конкурирующих точек,
принадлежащих скрещивающимся ребрам пирамиды. Пусть 3 [FF’] |
и |
||
4 [G’H’]. На Ï2 проекции этих точек 32 |
и 42 совпадают. |
Вопрос |
их |
видимости решается на Ï1: глубина точки 41 |
больше, чем у 31 |
(координата |
|
y4 > y3), следовательно, точка 4 расположена в пространстве перед точкой 3 и прикрывает ее собой. По видимости проекций точек определяется видимость соответствующих ребер на Ï2. Ребро [G2’H2’] видимое. Видимость остальных ребер понятна из чертежа.
3. Построение линии пересечения многогранника заданной плоскостью общего положения
Врезультате сечения поверхности плоскостью образуется линия, одновременно принадлежащая и поверхности, и плоскости. Такая линия называется линией пересечения поверхности плоскостью.
Замкнутая фигура, образованная линией пересечения поверхности тела секущей плоскостью, называется сечением и является частью секущей плоскости, заключенной внутри поверхности.
Вобщем случае линия пересечения многогранной поверхности с плоскостью представляет собой ломаную, т.е. линию, состоящую из прямолинейных отрезков, каждый из которых является линией
28
пересечения соответствующей грани многогранника (грань - часть плоскости) с секущей плоскостью. Напомним, что линия пересечения двух плоскостей - прямая.
Точки перелома ломаной являются точками пересечения ребер многогранной поверхности с секущей плоскостью. Следовательно, линию пересечения можно построить по точкам пересечения ребер многогранника с секущей плоскостью (задача на построение точки пересечения прямой с плоскостью общего положения - первая позиционная задача);
Решение задачи возможно двумя способами: с применением алгоритма первой позиционной задачи, с применением метода преобразования чертежа.
3.1. Построение линии пересечения многогранника заданной
плоскостью общего положения с применением алгоритма
первой позиционной задачи
Пусть в пространстве заданы плоскость α - секущая плоскость и прямая a – одно из ребер многогранника. Для решения вопроса об относительном положении прямой и плоскости через прямую à проводится
посредник - вспомогательная секущая плоскость β, строится линия пересечения b данной плоскости α с плоскостью β. При этом возможны следующие случаи относительного положения прямых à и b, лежащих в плоскости β:
1. Прямая b совпадает с прямой à. Т. к. прямая b, как линия пересечения плоскостей α и β, лежит в плоскости α, то в этом случае прямая à лежит в плоскости α. Пересечения нет. Прямая à полностью видима.
29
2.Прямая b параллельна à. В этом случае прямая à параллельна плоскости α. На чертеже прямая a или полностью видима, или полностью не видима по отношению к отсеку непрозрачной плоскости.
3.Прямая b пересекает à. В этом случае прямая à пересекает плоскость α. Точка Ê пересечения à с b принадлежит одновременно обеим прямым. Но т.к. прямая b лежит в плоскости α , то все ее точки, в том числе точка Ê, принадлежат этой плоскости. Следовательно, точка Ê
является единственной общей точкой для данных прямой à и плоскости α. Но такой точкой может быть только точка пересечения прямой с плоскостью. Часть прямой видима по отношению к непрозрачной плоскости, часть - нет. Пересечение имеет место.
Поясним сказанное на примере.
На комплексном чертеже построим точку Ê пересечения прямой
à (À, S), заданной точками A, S, с плоскостью α (m // n), заданной параллельными прямыми m и n, определим видимость прямой à относительно отсека плоскости (Рис. 14).
Дано: à (À, S) – о.п., α (m // n) – о.п.
Найти: Ê = à Ç α, определить видимость à.
Решение. Алгоритм нахождения точки Ê включает три этапа, результат которого показан на Рис. 14 a.
30
а |
б |
|
Рисунок 14 |
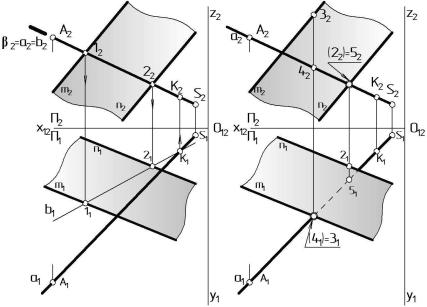
Этап 1. Прямую à (À, S) общего положения заключают во вспомогательную проецирующую плоскость-посредник. В данном случае это фронтально-проецирующая плоскость β( β2 ) ^ Ï2, которая на чертеже задается фронтальным следом β2 с указанием собирательного свойства следа отрезком утолщенной линии. След совпадает с проекцией прямой à2,
что отображается равенством β2 = à2. Проекция прямой à1 |
в этом этапе не |
|||
участвует. |
|
|
|
|
Этап 2. Находится линия пересечения b вспомогательной |
||||
проецирующей |
плоскости-посредника β с заданной |
плоскостью α: |
||
b(12) = β Ç α. Проекции прямой a в этом этапе не участвуют. |
|
|||
Фронтальная проекция b2 совпадает со следом плоскости-посредника |
||||
(β2 = b2) и пересекает прямые m2, n2 в точках 12 , 22: |
12 = β2 Ç m2; 22 = β2 Ç n2. |
|||
Горизонтальные проекции этих точек строятся по линии связи: |
11 Î m1; |
|||
21 Î n1. Отрезок |
1121 прямой b1, одновременно |
принадлежит |
обеим |
|
плоскостям и, следовательно, является линией их пересечения. |
|
|||
