
9286
.pdf
z |
(M |
) 3, |
z (M |
) 0 , |
z |
xx |
z |
yy |
(z |
xy |
)2 |
|
|
|
|
|
9 0 . Следовательно, |
M |
|
(0;0) - |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
xy |
1 |
|
yy |
1 |
|
|
|
|
|
|
|
|
|
|
|
M1 |
(0;0) |
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z (M |
|
|
z |
|
|
|
|
|||||
седловая точка. |
В |
точке |
M |
2 |
(1;1) : z |
(M |
2 |
) 6, |
2 |
) 3 , |
(M |
2 |
) 6 , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
|
xy |
|
yy |
|
|
|||||||
6 6 ( 3)2 |
27 0 , |
|
поэтому |
|
|
M |
2 |
(1;1) - |
|
точка |
минимума |
функции z; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zmin z(M2 ) 1.
Задача 8. (минимизация функции нескольких переменных методом Ньютона).
Минимизировать функцию f (х) методом Ньютона с заданной точностью
10 3.
f (х) х12 2х22 х12 х22 х32 ехр(х22 х32 ) х2 х3
101

102

103

Задачи для раздела 4.
Задача 1. Геометрический способ решения ЗНЛП
F (x1 3)2 (x2 4)2 min, max
104
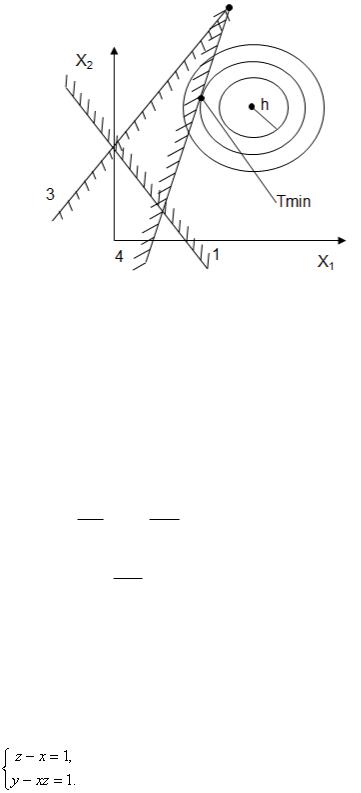
3x1 2x2 710x1 x2 8
18x1 4x2 12 x1, x2 0
(x1 3)2 (x2 4)2 h 2(x1 3) 2(x2 4)x2' 0
x' |
2(x1 3) |
|
x1 3 |
|
|
||||
2 |
2(x2 |
4) |
|
4 x2 |
|
|
|||
x1 3 10(4 x2 ) |
||||
|
|
8 |
|
|
10x1 x2 |
|
|
||
x1* 123101; x2* 101422
f (min) 324101 x**1 2, x**2 12, f (max) 65
Задача 2. (метод Лагранжа)
Методом Лагранжа найти экстремум функции 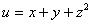 при условиях связи
при условиях связи
Решение. Составим функцию Лагранжа
105
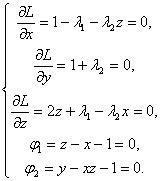
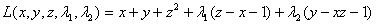 и рассмотрим систему уравне-
и рассмотрим систему уравне-
ний
Она имеет единственное решение 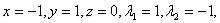 то есть
то есть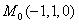 – единственная точка возможного экстремума функции при заданных условиях связи.
– единственная точка возможного экстремума функции при заданных условиях связи.
Вычислим второй дифференциал функции Лагранжа 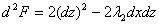 и подстав-
и подстав-
ляя 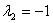 и
и 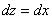 , найденное из первого уравнения связи, получаем положительно определенную квадратичную форму от переменной
, найденное из первого уравнения связи, получаем положительно определенную квадратичную форму от переменной 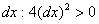 при
при 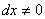 . Отсюда следует, что функция при заданных условиях связи имеет в точке
. Отсюда следует, что функция при заданных условиях связи имеет в точке 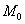 условный ми-
условный ми-
нимум.
Задача 3. (показывает, что в правиле множителей Лагранжа не всегда можно полагать 0 1).
32 fx,xxinf;fx,xxx0.
0121 11212
Решение. Функции f0 |
и f1 |
непрерывно дифференцируемы. Из условия |
|||||||
3 |
2 |
|
|
|
3 |
2 |
|
|
|
x x 0 следует, |
что x x 0 x 0. Поэтому очевидно, что решение задачи |
||||||||
1 |
2 |
|
|
|
1 |
2 |
1 |
|
|
x 0, 0 |
|
|
|
|
|
|
1 |
|
|
Если прямо следовать Лагранжу, то надо положить 0 |
|
, составить |
|||||||
|
. |
|
|||||||
|
|
|
|
|
3 2 |
|
|
|
|
сумму |
Lx x x |
|
далее решать систему |
|
уравнений |
||||
|
1 |
1 2 и |
|
||||||
L0 |
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
1 |
|
13x 0 |
|
|
|
|
|||
|
|
1 |
. Из последней системы следует, что 0 (так как в про- |
||||||
|
|
|
|||||||
|
|
|
|||||||
L0 |
2x0 |
|
|
|
|
||||
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
тивном случае не будет удовлетворяться первое уравнение системы), тогда решение
106

1
системы имеет вид: x , x0. Но при этих значениях x1, x2 не будет удо-
1 3 2
3 2
влетворяться уравнение связи x x 0. Таким образом, получим что решения
1 2
нет, а это неверно.
Задача 4. (показывает, что экстремум функции Лагранжа как задачи без огра-
ничений может не совпадать с экстремумом исходной задачи с ограничениями).
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
|
|
|
|
fx;xxxinf;fx;xxx0 |
|
|
||||||||||||||||||||||||||
|
|
|
|
01221 11211 |
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. Очевидно, |
|
что решение задачи x 0, 0 |
(так как |
|
из условия |
|||||||||||||||||||||||||||
|
3 |
|
|
что x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
0 ). Функ- |
|||||
x x 0 следует, |
0 , а решение задачи x |
inf имеет вид |
2 |
|
||||||||||||||||||||||||||||
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
ция Лагранжа записывается в виде: |
L xx xx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
02 1 1 1. Необходимое усло- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
L0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
|
13x 0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
вие экстремума: |
|
|
|
|
|
|
|
|
|
. Если |
0 |
|
|
, то |
|
|
|
|
|
и из первого |
||||||||||||
|
|
|
L 0 |
2x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
уравнения системы следует, что |
1 3x |
– противоречие. Значит, |
|
. Поло- |
||||||||||||||||||||||||||||
|
1 |
|
|
|
0 |
|
||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|||
жим |
. Тогда функция Лагранжа примет вид: |
Lx x xx |
|
|
||||||||||||||||||||||||||||
0 |
|
|
|
|
|
2 1 |
|
1 1. Очевид- |
||||||||||||||||||||||||
но, что |
L0, 0 0 |
Пусть 0 произвольное |
действительное |
|
число. Тогда |
|||||||||||||||||||||||||||
|
|
. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L,0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
L, 0 0 |
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
, при 0 и |
|
|
|
|
при |
|||||||||||
1) Если 0 , то 10. Тогда |
|
|
|
|
|
|
||||||||||||||||||||||||||
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Если 0 , |
то |
L, 0 |
|
|
L, 0 0 |
при 0 |
|
и |
L, 0 0 |
при |
||||||||||||||||||||||
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
1 |
|
L, 0 0 |
|
||||||||||||||||
3) |
Если 0 1, то |
при |
|
|
|
;0 |
|
при |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10; .
|
1 |
|
L, 0 |
|
L, 0 0 |
|
0 |
|
||
4) Если |
|
, то |
|
|
3 |
и, следовательно, |
|
при |
|
и |
|
|
|
|
|||||||
|
|
|
|
|
|
107 |
|
|
|
|
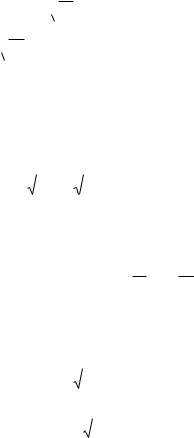
L, 0 0при 0 .
5) Если 1, то 210и, следовательно, L, 0 0 при 0 и
L, 0 0при 0 .
Таким образом, при любых функция L принимает в любой достаточно малой окрестности точки 0, 0 как положительные значения, так и отрицательные значе-
ния. А это означает, что ни при каких эта функция в точке x 0, 0 не имеет да-
же локального минимума. Значит, точка x 0, 0 не является решением задачи, а
это неверно.
Задача 5.
На развитие двух предприятий выделено 2 млн. рублей. Если первому предпри-
ятию дадут x1 млн. рублей, то прибыль, полученная от этого предприятия, будет
равна 2
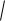 x1 млн. рублей, если x2 млн. дадут второму, то прибыль от него будет равна
x1 млн. рублей, если x2 млн. дадут второму, то прибыль от него будет равна
3
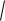 x2 млн. рублей. Определить, как следует распределить средства между предприя-
x2 млн. рублей. Определить, как следует распределить средства между предприя-
тиями, чтобы суммарная прибыль была максимальной. Решим эту задачу методом
множителей Лагранжа.
Задача |
состоит в отыскании точки глобального максимума функции |
|||
|
|
|
|
|
f 2 x1 + 3 |
x2 при ограничении x1 + x2 = 2 |
|||
Точку возможного максимума найдем методом множителей Лагранжа. Функ-
ция Лагранжа имеет вид:
L(x1, x2 , ) 2
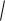 x1 3
x1 3
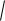 x2 (x1 x2 2)
x2 (x1 x2 2)
Для отыскания точек возможных экстремумов составим систему:
L |
|
1 |
|
|
0 |
|||||
|
|
|
|
|||||||
|
x1 |
|
|
x1 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
3 |
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
x2 |
|
2 |
|
x2 |
|
|||||
|
|
|
|
|
||||||
L |
x x |
|
|
2 0 |
||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
108

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
x |
||||||||||||||||
|
Найдем ее решение. |
|
|
|
|
|
|
|
2 |
x |
|
|
3 |
x |
x |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 |
|
x2 |
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
4 1 |
|||||||||||||||
|
Подставим |
|
найденное |
соотношение |
|
|
x |
|
|
9 |
x |
в |
|
уравнение (3), получим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
1 |
|
|
|
|
|
|
x |
9 |
x |
2 0 |
13 |
|
x 2 x |
|
8 |
|
и тогда x |
|
|
18 |
|
. Находим : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Итак, система имеет одно решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
8 |
|
|
18 |
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
P0 |
|
|
|
|
|
; |
|
|
|
|
|
|
; 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
13 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Исследуем найденную точку на локальный условный экстремум с помощью |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определителя L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
y x1 , x2 x1 x2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
y |
1; y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
L |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x1 |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
L 2 |
|
|
|
|
1 |
|
|
|
; L |
|
P |
|
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
|
|
32 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
L |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
L |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x2 |
|
|
|
|
2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
L |
|
|
|
|
|
|
3 |
|
|
|
; L |
|
P |
|
|
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
x2 |
|
0 |
|
|
|
72 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставив все в формулу получаем
0
1 1
1
Так как
1
13 13
32 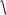 2
2
0
0 , то
|
|
|
1 |
|
|
|
|||
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
13 |
|
|
13 |
|||||
|
|
|
|
|
|
||||
72 |
|
|
|
|
|
2 |
|
||
8 |
|
|
18 |
|
|||||
Po |
|
; |
|
|
|
|
|||
|
|
|
|
||||||
13 |
|
|
13 |
|
|||||
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
13 |
|
13 |
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
|
13 |
|
13 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
32 |
|
2 |
|
|
|
|
|
|
72 |
|
2 |
|
|
32 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
72 |
|
2 |
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
– точка локального условного максимума.
109
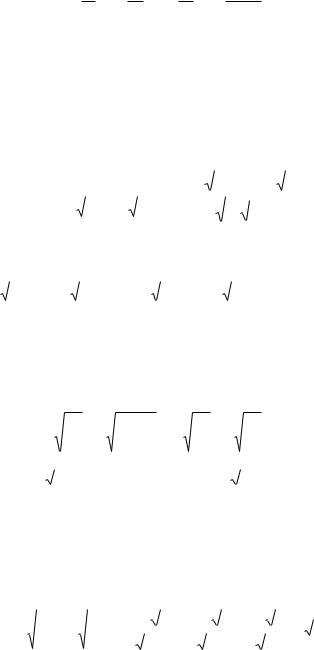
Чтобы показать, что именно в точке Po достигается и глобальный максимум,
перейдём к задаче на отыскивание безусловного максимума функции одной пере-
менной. С помощью задачи x1 x2 2 , запишем условную функцию в виде:
f (x1, x2 ) 2
 x1 3
x1 3
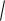 x2 2
x2 2
 x1 3
x1 3
 2 x1 y(x1 )
2 x1 y(x1 )
Требуется найти такую точку, где достигается наибольшее значение функции.
Область возможного изменения оставшейся переменной отрезок [0;2].
Непрерывная функция на замкнутом отрезке обязательно достигает своего наибольшего значения либо в критических точках внутри отрезка, либо на концах
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отрезка: y (x1 ) |
1 |
|
|
|
|
3 |
|
|
|
2 2 x1 3 x1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x1 |
|
|
|
2 2 x1 |
|
2 x 2 x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из условия y (x1 ) 0 находим стационарную точку |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
(0;2) |
||||||||||||||
2 2 x 3 |
|
x |
0 2 |
2 x |
|
3 x |
4(2 x ) 9x |
8 4x |
9x |
13x |
8 x |
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
13 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Точек, где производная не существует, внутри отрезка нет. Находим значение
целевой функции в стационарной точке и на концах отрезка.
y( |
8 |
) 2 |
18 |
|
3 |
2 |
8 |
|
2 |
8 |
|
3 |
18 |
|
1,56 3,35 5,09 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
13 |
13 |
|
|
13 |
|
13 |
|
13 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
y(0) 3 |
2 4,24 |
|
|
|
|
y(2) 2 |
2 2,83 |
|||||||||||||
Мы видим, что наибольшее значение достигается в точке x |
|
8 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
13 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
И так, глобальный максимум достигается при x |
8 |
млн.руб., x |
|
|
|
18 |
|
млн.руб. |
|||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
13 |
|
|
|
13 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8 |
|
|
18 |
|
|
2 2 |
2 |
|
3 3 |
2 |
|
13 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y 2 |
|
3 |
|
|
|
|
|
26 5,09млн.руб. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Задача 6. (метод штрафных функций)
x12 + x22 min x1 + x2 -1= 0
110
