9278

200

§11. Основные определения, классификация волн

Волновые процессы, или волны окружают нас повсюду: волны на воде - поверхностные волны, звуковые волны, электромагнитные волны (в частности, видимый свет, излучение тепла нагретым телом) — это далеко не полный перечень волновых процессов. Мы ограничимся весьма кратким рассмотрением этого класса физических явлений.

Итак, волной называют колебание какой-то физической величины, распространяющееся в пространстве, т.е. волна – это бегущее колебание. Если колебание описывалось функцией одного аргумента - времени, то волна есть функция

по крайней мере двух переменных - времени и пространственной координаты (в

общем случае всех координат x, y, z).

Геометрическое место точек пространства, где колебания имеют одинаковую фазу, называется волновой поверхностью, а первая (т.е. наиболее удаленная от источника) волновая поверхность – волновым фронтом.

Виды волн 1. По форме волнового фронта различают плоские, сферические, цилиндрические

волны.

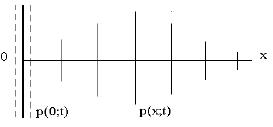
Плоские волны создаются плоским излучателем, имеющим достаточно большие размеры (формально - бесконечной плоскостью). Если такая волна распространяется вдоль оси x, то она описывается функцией двух переменных p(x;t).

Сферические волны создаются источником сферической формы. Например, источником таких звуковых волн может служить динамик с диффузором в виде шара. Заметим, однако, что на больших расстояниях (значительно превышающих размеры источника) волна будет сферической при любой форме источника колебаний. Другими словами, источник колебаний малых размеров излучает сферические волны.

Такие волны описываются функцией p(r;t) , где r - расстояние от источника.

Предположим, что источник совершает гармонические колебания с частотой £ = 1/t = U/2—, где T - период колебаний, ω - циклическая частота.

201

Расстояние, пробегаемое волной за один период колебания, называется

длиной волны:

ó = (t = £(,

где c - скорость распространения волны.

2.По форме распространяющихся колебаний различают гармонические (в оптике их называют монохроматические) и негармонические волны. Последние можно представить суперпозицией гармонических.

3.По физической природе различают упругие (или звуковые) волны, поверхностные

(например, волны на воде), электромагнитные и другие.

Естественно, характеристики перечисленных волновых процессов совершенно различны. Они различны и внутри любого одного типа волн; например, различна скорость звука в газах и жидкостях, свойства электромагнитных волн существенно зависят от их частоты. Однако, как и в случае колебаний, в математическом описании волн разных видов много общего.

4.По направлению колебаний различают волны продольные и поперечные. Для первых направление колебаний совпадает с направлением распространения волны, для вторых - эти направления взаимно перпендикулярны. Например, звук в газах - это продольные волны, электромагнитные волны – поперечные

§12. Плоские и сферические волны

Предположим, что в плоскости x = 0 имеется источник, совершающий колебания; например, для звуковых волн, это может быть плоскость диффузор громкоговорителя. Считаем эти колебания гармоническими с амплитудой A и циклической частотой ω

(12.1)

202

При этом в упругой среде (газе, жидкости) колебания давления (или плотности), вызванные колебаниями источника p(0; t), передаются от точки к точке, и вдоль оси x побежит плоская волна p(x; t), (рис.13).

Рис.13. Распространение плоской волны

Пренебрегая затуханием колебаний по мере их распространения, считаем, что колебание, которое пришло в точку x в момент времени t - это то же, что было в точке

Ясно, что для волны, бегущей влево в выражении (12.2) следует поставить знак + (т.к. изменится знак скорости).

Наблюдая волну (12.2) в фиксированной точке x=x1, мы имеем гармоническое

это осциллограмма плоской волны. Зафиксировав в (44) момент времени t=t1,

получим гармоническую функцию координаты, называемую мгновенный снимок волны

Период этой функции равен длине волны λ.

204

среды в твердом теле, из газовых законов при исследовании распространения колебаний давления в газе, из уравнений электродинамики в задачах распространения электромагнитных волн. Конечно, в разных задачах физический смысл переменной p c различен.

Отметим, что гармоническая волна (12.2) это лишь одно из его решений. Оказывается, ему удовлетворяет колебание любой формы, бегущее со скоростью с. В самом деле, пусть колебание источника представляет собой любую функцию времени, т.е. p(0;t)= f(t). Тогда в точке x оно имеет вид p(x,t)= f(t-x/c) . Обозначим z =t-

§14. Звуковые волны

Звуковые волны в газе представляют собой бегущие колебания давления p (или плотности, поскольку, согласно уравнению состояния газа, они пропорциональны). Если атмосферное давление равно pA, то полное давление в точке x, которую достигла плоская волна в момент времени t, будет P(x;t) =pА+ p(x,t), где p(x,t) - малая добавка, определяемая формулой (12.2).

Человек слышит не любой звук, а примерно, в диапазоне частот от 20 герц до 20 килогерц. Колебания более низких частот называют инфразвуком, а более высоких

- ультразвуком. Скорость распространения звуковых волн в газе зависит от плотности среды (а она связана с температурой) и определяется формулой

( = √Å q = ¢Å šy, (14.1)

± [

где γ - показатель адиабаты (для воздуха он равен 1,4), R – газовая постоянная, μ - молярная масса (для воздуха - 0,029 кг/моль). При нормальных условиях формула (14.1) даёт значение скорости звука c = 330м/с.

Звуковые волны в твердых телах могут быть как продольными, так и поперечными (сдвиговыми). Скорость распространения звука в твердых телах

205

зависит от их упругости и плотности, и она значительно выше скорости звука в

где E - модуль упругости (модуль Юнга), G - модуль сдвига, ρ - плотность материала. Например, для железа формула (14.2а) дает значение c = 5170 м/с.

Слуховое восприятие звуковых волн - громкость зависит от интенсивности колебаний ß = =/ , где p - средняя мощность колебаний, переносимая через площадь S. Интенсивность пропорциональна квадрату амплитуды колебаний, а наше восприятие громкости - логарифму интенсивности. Принятая в акустике единица измерения интенсивности звука – децибел ориентирована именно на логарифмическое восприятие. Скажем, если интенсивность в единицах системы СИ

равна I (Вт/м2), то в децибелах она равна

ß»ç = 10lg(ãã•),

где I0 - минимальная интенсивность, соответствующая порогу слышимости (примерно 10 -12 Вт/м2)

§15. Электромагнитные волны

Электромагнитные волны представляют собой взаимно связанные колебания напряженности электрического и магнитного полей, распространяющиеся в пространстве. Источником электромагнитных волн являются движущиеся с переменной скоростью электрические заряды. Это могут быть хаотически движущиеся свободные электроны или ионы (в случае теплового излучения), переменный ток достаточно высокой частоты в проводнике (при излучении радиоволн), электроны, переходящие с верхних энергетических уровней на нижние (при излучении света газоразрядными трубками и лазерном излучении).

Электромагнитные волны могут распространяться в свободном пространстве (вакууме) или в средах не проводящих электрический ток. В проводящей среде они

в тепло и волны быстро затухают. Скорость электромагнитных волн в вакууме с=3 108 м/c, её принято называть скоростью света. В среде с показателем преломления n

скорость их меньше.

= {( , { = ì•/m.

Здесь ε - диэлектрическая, а μ - магнитная проницаемость. В диэлектрических средах, где, собственно, и могут распространяться волны, μ=1.

Электромагнитные волны поперечные: если, например, волна бежит вдоль оси OX,

то колебания вектора напряженности электрического поля Ñ направлены вдоль оси

OY, а колебания напряженности магнитного поля ² - вдоль оси OZ (или наоборот). Соответствующие формуле (13.1) волновые уравнения здесь имеют вид:

Существование электромагнитного поля и связанных с ним электромагнитных волн было теоретически обосновано Максвеллом в 1860 году, а экспериментально обнаружены они были спустя примерно полвека Герцем. Практическое использование электромагнитных волн в современном мире постоянно растет. Приведем в заключение шкалу электромагнитных волн, где длине волны примерно соответствует указанный характер электромагнитного излучения.

Рис.14. Шкала электромагнитных волн

Отметим, что видимый свет ограничен диапазоном длин волн 3,6 ∙ 10ij ≤ ó ≤ 7,7 ∙ 10ij м. Нижняя граница соответствует фиолетовому цвету, верхняя - красному. Излучение на длинах волн справа от этого интервала называется инфракрасным (воспринимается, как тепло), а слева от него - ультрафиолетовым.

208

Подставим в выражение для периода момент инерции стержня и расстояние d :

lпр ≈ 1,18 м.

Ответ: T ≈ 2,2 c, lпр ≈ 1,18 м.

Задача 2. Точка одновременно участвует в двух взаимно перпендикулярных

колебаниях, происходящих по законам: x =cosπt , y = cos π t . Определить уравнение

2

2время. Преобразуем уравнение движения вдоль оси x ,

значит:

y2 = cos2 π t . 2