
8803
.pdfб) ∑ 0, |
∑ 0, |
∑ 0, если точкиАи В не лежат на одном пер- |
пендикуляре к оси X; |
|
|
в) ∑ 0, |
∑ 0, |
∑ 0, если точкиА, В и С не лежат на одной |
прямой. |
|
|
Для сочлененных рам необходимо к этим уравнениям дополнительно составить условия равновесия отдельных частей в виде
∑ш шодн.с. 0,
где Ш - число простых шарниров.
Следовательно, для статически определимой рамы, имеющей Ш простых шарниров, можно составить Ш + 3 уравнения статики для определения опорных реакций.
2. Определение внутренних усилий - изгибающего момента , поперечной силы
и продольной сил в характерных сечениях рамы.
Изгибающим моментом называется сумма статических моментов всех од- носторонних сил от рассматриваемого сечения относительно центральной оси рас- сматриваемого сечения перпендикулярной силовой плоскости.
Поперечной силой называется сумма проекций всех односторонних сил от рас- сматриваемого сечения на ось, перпендикулярную оси стержня и лежащую в силовой плоскости.
Поперечная сила считается положительной, если вызывает вращение отсеченного элемента по часовой стрелке.
Продольной силой называется сумма проекций всех односторонних сил от рас- сматриваемого сечения на ось стержня.
Продольная сила считается положительной, если вызывает растяжение отсеченного элемента, и отрицательной, если - сжатие.
На основании этих определений и способа простых сечений вычисление внутренних усилий в сечениях стержней производится из уравнений равновесия статики
∑ 0, ∑ 0, ∑М 0, составленных для отсеченной части рамы, находящейся в равновесии под действием внешних сил и внутренних усилий.
При рассмотрении равновесия той или иной отсеченной части системы неизвестный изгибающий момент принимается любого направления, а неизвестные поперечная и продольная силы только положительными. Если в результате решения изгибающий момент получился отрицательным, то это значит, что растянуты противоположные волокна в стержне по отношению к первоначально принятому.
При определении усилий в сечениях отсеченной части рекомендуется рассматривать равновесие той системы, на которую действует меньшее число силовых факторов.
3. Построение эпюр изгибающих моментов, поперечных и продольных сил. При построении эпюр внутренних усилий по вычисленным в характерных сечениях значениям необходимо иметь в виду следующие особенности:
а)ординаты эпюр откладываются перпендикулярно оси стержня: в эпюре - со стороны растянутого волокна без указания знаков; в эпюре - с двух сторон от оси стержня; в эпюре - симметрично от оси стержня с указанием знаков;
б) каждый узел рамы должен находиться в равновесии; 21

в) на прямолинейном незагруженном участке рамы изгибающий момент всегда изменяется по линейному закону, а поперечная и продольная силы постоянны;
г)при действии на элемент равномерно распределенной нагрузки изгибающий момент изменяется по закону квадратной параболы, поперечная сила - по линейному закону, а продольная сила постоянна, если действующая нагрузка перпендикулярна оси стержня, и изменяется по линейному закону, если нагрузка не перпендикулярна оси стержня;
д) если на элемент системы действует нагрузка в виде сосредоточенной силы, то в том сечении, где она приложена, на эпюре будем иметь точку излома в сторону прило-
жения силы; на эпюре скачок на величину этой силы, если она перпендикулярна оси стержня, и на величину проекции этой силы на ось; перпендикулярную оси стержня, если нагрузка не перпендикулярна оси элемента. На эпюре скачок будет только в том слу-
чае, если нагрузка не перпендикулярна оси стержня, и его величина будет равна проекции этой силы на ось стержня.
е) если на элемент рамы действует нагрузка в виде сосредоточенного момента, то в том сечении, где он приложен, на эпюре будет скачок на величину этого момента с па-
раллельными ветвями, очерчивающими эпюру; на эпюры и эта нагрузка влияния не оказывает;
ж) между изгибающим моментом и поперечной силой существует известная зави-
симость dMp = Q , согласно которой, если эпюра на рассматриваемом участке нисходя-
dx p
щая, то положительна, если эпюра восходящая,то отрицательна.
Построив эпюры , и , необходимо выполнить статическую проверку, кото-
рая состоит в том, что любая отсеченная часть рамы должна находиться в равновесии и, таким образом, должны выполняться условия равновесия статики.
6.2Графическое (эскизное) построение эпюр изгибающих моментов
Вэтом разделе рассматривается графическое построение эпюр изгибающих моментов в статически определимых рамных системах. При заданных форме, характере опорных связей и размерах рамы можно графически определить величины и направление опорных реакций, их равнодействующих, и на основании определения изгибающего момента графически построить соответствующую эпюру. Такое решение позволяет достаточно быстро установить закон распределения усилий в инженерных сооружениях и, в частности, в рамах. Здесь рассмотрено построение эпюр изгибающих моментов при простых случаях загружения: сосредоточенной силой, моментом или нагрузкой, распределенной на участке. При действии нескольких видов силовых факторов построение эпюры
производится методом наложения.
Литература: [1, гл. 1]; [4, гл. 1]; [2, гл. 1]; [3, гл. 3. 3-3.5].
Вопросы для самопроверки:
1.Что такое изгибающий момент в сечении?
2.Что такое поперечная сила в сечении? Когда поперечная сила считается положительной?
3.Что такое продольная сила в сечении? Когда продольная сила считается положительной?
22
4.Что называется эпюрой внутренних усилий?
5.Графическое (эскизное) построение эпюр изгибающих моментов.
7. Многопролётные статически определимые балки
Многопролетной статически определимой балкой называется геометрически неизменяемая статически определимая система, состоящая из однопролетных балок, соединяемых между собой полными идеальными шарнирами.
Многопролетной статически определимой балкой называется геометрически неизменяемая статически определимая система, состоящая из однопролетных балок, соединяемых между собой полными идеальными шарнирами.
Необходимым условием геометрической неизменяемости балки является равенство нулю ее степени свободы W=3D– Ш– Со=0. Число дисков D или отдельных балок зависит от количества шарниров Ш, т.е. D= Ш +1. Поэтому выражение 3(Ш + 1) –2 Ш – Со = 0 позволяет получить необходимое условие геометрической неизменяемости многопролетной статически определимой балки в виде:
Ш = Со–3, (7.1)
где Со - число опорных связей.
7.1 Образование многопролетных статически определимых балок
Необходимое количество шарниров должно быть расположено таким образом, чтобы система во всех своих частях была геометрически неизменяемая и статически определимая.
Существует три способа расположения шарниров в пролетах балки
1)постановка по одному шарниру в пролете (рис.7.1 а);
2)шарниры располагают по два через пролет (рис.7.1 б);
3)комбинированная постановка шарниров (рис.7.1 в).
Для соблюдения условий статической определимости и геометрической неизменяемости во всех частях таких балок при их конструировании необходимо выполнять следующие правила:
1.В каждом пролете должно быть не более двух шарниров.
2.Пролеты с двумя шарнирами следует чередовать с пролетами без шарниров.
3.Если крайняя опора шарнирная, то в примыкающем пролете может быть установлено не более одного шарнира.
4.Если крайняя опора имеет заделку, то в примыкающем пролете должно располагаться не менее одного шарнира.
23
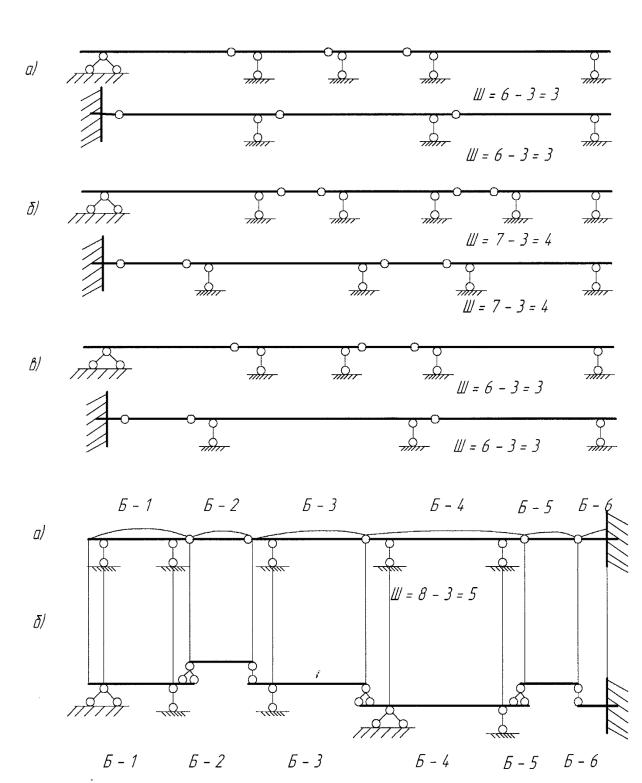
5. Для того чтобы балка была неподвижной, в горизонтальном направлении достаточно одной связи первого вида.
Рис. 7.1
24
7.2. Аналитический расчет многопролетных статически определимых балок
на неподвижную нагрузку
Существует два способа расчета балок: способ расчета балки в целом как статически определимой системы и способ расчета балки путем построения поэтажной схемы.
1.Способ расчета балки в целом как статически определимой системы заключается
вопределении опорных реакций из условий сопряжения балок в шарнирах и уравнений равновесия всей системы. Построение эпюр изгибающих моментов и поперечных сил выполняется, как в статически определимых системах. Такой путь решения слишком громоздкий. Способ расчета балки путем построения поэтажной схемы является более удобным.
2.Расчет многопролетной статически определимой балки с применением поэтажной схемы.
При правильной постановке пролетных шарниров многопролетная балка разделяется на ряд однопролетных статически определимых балок (рис.7.1 а). Характер взаимодействия между балками может быть выявлен в поэтажной схеме, где можно выделить два вида балок: основные и вспомогательные (рис.7.1 б). Основные балки (Б-1, Б-4, Б-6) крепятся тремя связями непосредственно к основанию. Вспомогательные балки (Б-2, Б-3, Б-5) опираются на основные.
При изображении поэтажной схемы балки следует иметь в виду, что нарушается общая горизонтальная связь балки, поэтому в каждой простой балке необходимо показывать все три связи, необходимые ей для геометрической неизменяемости и статической определимости.
По условиям работы балки разделяются на независимые и зависимые. Независимые балки (второстепенные)способны воспринять только местную на-
грузку, расположенную в пределах их длины.
Зависимые балки(основные) - это такие, которые испытывают действие не только нагрузки, расположенной непосредственно на них, но и давление со стороны смежных (второстепенных) балок, на них опирающихся.
В поэтажной схеме (рис.7.2 б) балки Б-2 и Б-5 являются независимыми, а остальные - зависимыми.
Поэтажная схема балки определяет порядок расчета балки как совокупности однопролетных балок. Расчет начинают с независимых балок, начиная с самых верхних балок. Затем рассчитывают зависимые балки.
Расчет каждой балки выполняется в следующей последовательности:
1.Определение опорных реакций.
2.Вычисление изгибающих моментов в необходимых для построения эпюры сече-
ниях.
3.Вычисление поперечных сил в характерных сечениях.
При расчете зависимых (основных) балок необходимо учесть давление вышележащих балок, опирающихся на зависимые (основные) балки.
Сила, с которой верхняя балка действует на рассматриваемую балку, равна по величине реакции верхней балки и имеет противоположное направление.
25
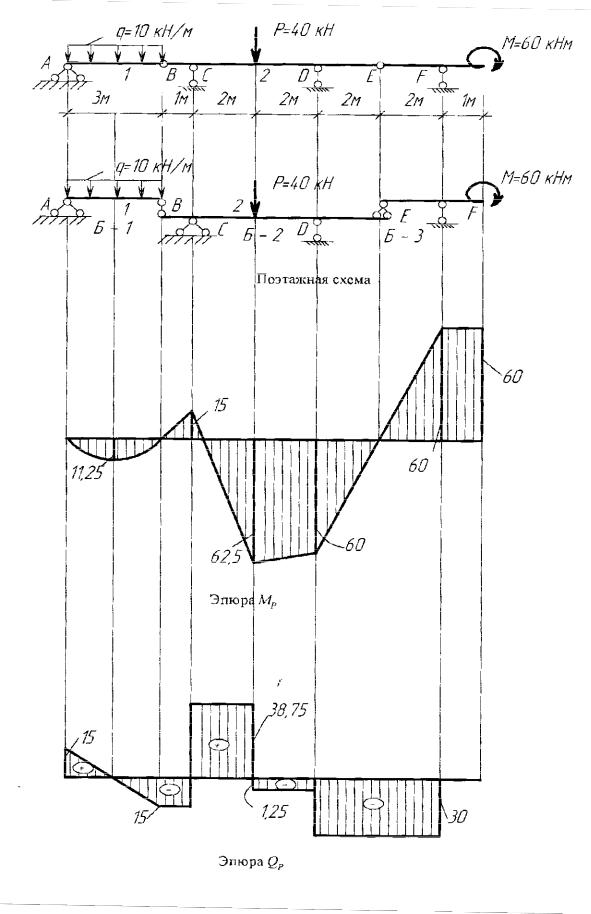
Рис.7.2
26
Задания для самостоятельной работы.
Литература: [1, гл. 1]; [4, гл. 1]; [2, гл. 1]; [3, гл. 3. 3-3.5].
Вопросы для самопроверки:
1.Как необходимо строить поэтажную схему?
2.Какие балки называются зависимыми и какие независимыми?
3.С какой балки надо начинать расчет в поэтажной схеме?
8.Основы расчета сооружений на подвижную нагрузку
8.1. Общие сведения
При расчете на подвижную нагрузку приходится решать задачи двоякого рода: вопервых определять те или иные величины (опорные реакции, поперечные силы, изгибающие моменты в балках или усилия в элементах ферм) при заданном расположении нагрузки и, во-вторых, находить наиболее невыгодное расположение нагрузки, т.е. выбирать такое ее положение, при котором искомые величины достигнут наибольшего значения.
Так, для двухопорной балки при действии на неё подвижной нагрузки P , изгибающий момент в сечениях, расположенных левее груза
P , т.е. при z ≤ x , выразится следующим обра-
зом: M c |
= |
P × (l - x) |
× z , а в сечениях, |
распо- |
|
||||
|
|
l |
|
|
ложенных правее груза P, т.е. при |
z ³ x |
|||
M c = P × x × (l - z) . Таким образом, при дейст- l
вии на сооружение подвижной нагрузки любая изучаемая величина будет являться функ-
цией двух переменных: S = f (x, z) , где x –
координата, определяющая положение на сооружении подвижной нагрузки, z – координата, определяющая положение сечения, в котором определяется изучаемая величина.
Эту функцию называют функцией влияния. В пространстве эту функцию можно представить в виде поверхности влияния.
Если поверхность влияния рассечь семейством плоскостей x = ai , i = 1, 2, . . . n, параллельных плоскости soz, то их линии пересечения будут представлять собой эпюры.
Если же рассечь поверхность влияния семейством плоскостей z = bi , i = 1, 2, … n, параллельных плоскости sox , то линии их пересечения будут представлять собой инфлю-
ентные линии или линии влияния.
Эпюрой называют график изменения изучаемой величин в различных сечениях рас- сматриваемой конструкции при действии на нее неподвижной (статической) нагрузки.
27
Линией влияния называют график зависимости искомой величины (силы, напряже- ния, перемещения и т.п.) от положения единичного груза (P = 1) постоянного направле- ния.
Таким образом, принципиальная разница между эпюрой и линией влияния в следующем:
-в эпюре подвижно сечение и неподвижен груз (нагрузка). В линии влияния неподвижно сечение, а подвижен единичный груз;
-ординаты эпюры связаны с сечением, а ординаты линии влияния связаны с подвижным грузом;
-ординаты эпюры выражают изучаемую величину в различных сечениях конструкции при неподвижной нагрузке, а ординаты линии влияния выражают изучаемую величину в одном и том же сечении при различных положениях единичного подвижного груза.
При построении линий влияния используют единичный подвижный груз, так как имея расчет на действие именно единичной сосредоточенной силы мы можем легко определить изучаемую величину при действии на конструкцию любой другой нагрузки. Это возможно, во-первых, потому, что именно из сосредоточенных сил можно получить любую нагрузку, в том числе и распределенную, путем предельного перехода к бесконечной сумме малых сосредоточенных сил. Во вторых, в линейно деформируемых системах (дей-
ствует закон Гука σ = E × ε ) справедлив принцип независимости действия сил (принцип
наложения), который формулируется так: если на конструкцию действует несколько ви- дов нагрузок, то суммарный результат этих нагрузок равен сумме результатов каждой отдельной нагрузки. Это относится к опорным реакциям, усилиям, деформациям, перемещениям и другим расчетным величинам. Т.е. :
|
n |
|
Vi = Vi1 + Vi 2 + ... + Vii = ∑Vik , |
|
k =1 |
где: Vi – |
эффект воздействия системы сил P1, P2, … , P i, …, P n ; |
Vii – |
эффект воздействия силы Pi . |
В обозначении Vik первый индекс показывает где определяется изучаемая величина, |
|
второй индекс – |
от какого воздействия определяется эта величина. |
Используя далее принцип пропорциональности, т. е. представляя каждое слагаемое условия принципа независимости действия сил в виде произведения соответствующей
__ |
|
изучаемой величины от единичного воздействия Vik , увеличенной в Pk |
раз, т.е. |
__
Vik = Vik × Pk , получим принцип суперпозиции:
__ |
__ |
__ |
__ |
n |
__ |
Vi = V i1 |
× P1 +V i 2 |
× P2 +… + V ii × Pii + … + V in × Pn = ∑ |
V ik × Pk . |
||
k =1
Для построения линий влияния усилий в элементах статически определимых систем существует ряд методов, из которых наиболее распространенными являются стати-
ческий и кинематический.
28
8.2. Статический метод построения линий влияния усилий в статически определи-
мых системах
Этот метод основан на использовании уравнений равновесия статики. Для построения линии влияния груз P = 1 устанавливают в произвольное положение, считая абсциссу точки его приложения x переменной величиной. Далее, на основании условий равновесия статики, выражают изучаемую величину. В результате получают уравнение ветви линии влияния. В ряде случаев приходится устанавливать груз поочередно на несколько участков, для каждого из которых выводить свое уравнение ветви. В этом случае общая линия влияния будет состоять из отдельных линий влияния, построенных для каждого участка на основании своих уравнений ветвей.
Проиллюстрируем сказанное на примере простой двухопорной статически определимой балки.
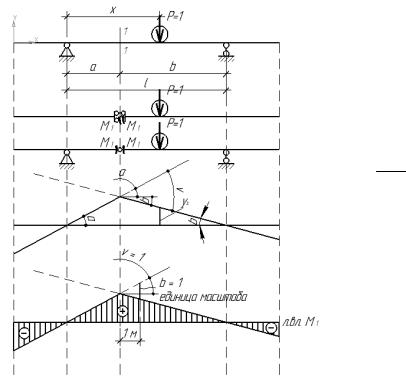
Выберем начало отсчета в точке А и обозначим переменное расстояние от начала координат до точки приложения груза P = 1 через x.
Линия влияния опорных реакций
Составим аналитическое выражение реакции в опоре А от подвижного груза P = 1,
используя уравнение ∑M B = 0 :
RA × l - P × (l - x) = 0 , RA |
= |
P × (l - x) |
= |
l - x |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
l |
|
l |
|
|
|
||
Изобразим графически это уравнение. При x = 0 RA = 1; при x = l RA = 0. |
|||||||||
По найденным значениям построим график – |
линию влияния реакции RA. |
||||||||
Из уравнения ∑M A = 0 получим: RB × l - P × x = 0 , |
RB = |
P × x |
= |
x |
. При x = 0 |
||||
l |
|
||||||||
|
|
|
|
|
|
l |
|||
RB = 0; при x = l RB = 1. По найденным значениям строим линию влияния реакции RB. Ординаты линий влияния опорных реакций выражаются в отвлеченных (безраз-
мерных) единицах, поэтому при построении графиков отрезки, равные единице, отклады-
ваются в произвольном масштабе. Любая ордината каждого из графиков выражает со- ответствующую опорную реакцию, если единичный подвижный груз встанет над этой ординатой.
Линия влияния поперечной силы
Для построения линии влияния поперечной силы в изучаемом сечении 1-1 рассмотрим два положения подвижного груза P = 1 относительно сечения.
- Груз находится правее изучаемого сечения 1-1, т.е. a ≤ x ≤ l . Рассматривая рав-
новесие левой отсеченной части балки, будем иметь:
Q |
= R |
|
= |
l - x |
|
- уравнение правой ветви линии влияния, которая справедлива |
||
A |
|
|
||||||
1−1 |
|
|
|
l |
|
|||
|
|
|
|
|
|
|||
от правой опоры до изучаемого сечения. |
||||||||
- Груз находится левее изучаемого сечения 1-1, т.е. 0 ≤ x ≤ a . Рассматривая рав- |
||||||||
новесие правой отсеченной части балки, будем иметь: |
||||||||
Q |
= - R |
|
= - |
x |
- уравнение левой ветви линии влияния, которая справедлива |
|||
B |
|
|||||||
1−1 |
|
|
|
|
|
|
|
|
l
от левой опоры до изучаемого сечения.
29

Полученные ветви линии влияния параллельны друг другу и в изучаемом сечении 1-1 график претерпевает разрыв непрерывности на величину, равную единице.
Ординаты линии влияния поперечной силы измеряются в отвлеченных единицах (безразмерные).
Линия влияния изгибающего момента
Для построения линии влияния изгибающего момента в изучаемом сечении 1-1 также рассматриваем два положения подвижного груза P = 1.
- Груз находится правее изучаемого сечения, т.е. a ≤ x ≤ l . Рассматривая равнове-
сие левой отсеченной части балки, будем иметь:
RA × a - М1−1 = 0 , M 1−1 |
= RA |
× a = |
l − x |
× a - уравнение правой ветви линии влия- |
|
||||
|
|
|
l |
|
ния, справедливой на участке от правой опоры до изучаемого сечения 1-1.
- Груз находится левее изучаемого сечения, т.е. 0 ≤ x ≤ a . Рассматривая равнове-
сие правой отсеченной части балки, будем иметь:
- RB ×b + М1−1 = 0 , M 1−1 |
= RB |
× b = |
x |
× b - уравнение левой ветви линии влияния, |
|
||||
|
|
|
l |
|
справедливой на участке от левой опоры до изучаемого сечения 1-1.
Из полученных выражений ветвей линии влияния изгибающего момента в сечении 1-1 следует, что когда груз P=1 перемещается на участке от правой опоры до сечения, то линия влияния M1-1 изменяется по закону опорной реакции RA, ординаты которой следует увеличить в (a) раз.
Когда груз P=1 перемещается на участке от левой опоры до сечения, то линия влияния M1-1 изменяется по закону опорной реакции RB , ординаты линии влияния которой следует увеличить в (b) раз. Таким образом, для построения линии влияния изгибающего момента в сечении 1-1 необходимо на вертикалях опор вместо отвлеченных единиц отложить отрезки “a” – на левой опоре и “b” – на правой опоре и соединить их с нулевыми точками на противоположных опорах. При этом, правая и левая ветви линии влияния изгибающего момента всегда будут пересекаться под изучаемым сечением (это несложно доказать, рассматривая подобие треугольников).
Каждая ордината полученного графика будет выражать собой значение изги- бающего момента в сечении 1-1, когда груз встанет над этой ординатой.
Ординаты линии влияния изгибающего момента измеряются в единицах длины.
Размерность ординат линии влияния равна отношению размерности изучаемой по линии влияния величины к размерности подвижного груза.
Рассмотрим построение линий влияния усилий для консольной балки.
Из уравнения ∑ y = 0 следует, что RA = P = 1, т.е. величина реакции в опоре A не
зависит от положения подвижного груза P = 1 и будет величиной постоянной.
Пусть груз P = 1 находится справа от сечения 1-1. В этом случае поперечная сила в изучаемом сечении Q1-1 =1.
При положении груза P = 1 слева от сечения, поперечная сила Q1-1 = 0.
30
