
8785
.pdf
40
5.6.ЗАВИСИМОСТЬ ГЛАВНОГО МОМЕНТА ОТ ВЫБОРА ТОЧКИ ПРИВЕДЕНИЯ
Пусть задана произвольная система сил (рис. 5.5), главный момент которой относительно центра А равен
|
A |
|
∑ |
A ( i ) |
|
∑( i |
i ) |
||
R |
|
= |
n |
R |
R |
= |
n |
R |
R |
M |
|
i=1 |
M |
F |
i=1 |
r |
× F . |
||
|
|
|
|
|
|
|
|
||
Выберем новый центр приведения − точку B, относительно которой положе-
R
ние старого центраA определяется радиус-вектором r0 , а положение некоторой i-й
силы системы − радиус-вектором R′ , который равен
ri
R′ = R + R
ri r0 ri
Определим главный момент системы сил относительно нового центраB.
|
B |
∑ |
|
B ( |
i ) |
∑( i |
|
i ) |
|
∑( |
0 |
i i ) |
|
∑( 0 |
i ) |
∑( i |
i ) |
||||
R |
|
n |
R |
|
R |
n |
R′ |
R |
|
n |
R |
R |
R |
|
n |
R |
R |
n |
R |
R |
|
M |
|
= M F = |
|
|
= |
|
|
= |
|
× F + |
|
× F . |
|||||||||
|
|
i=1 |
r |
× F |
i=1 |
(r |
+ r )× F |
i=1 |
r |
i=1 |
r |
||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Первое слагаемое представляет собой векторное произведение радиус-вектора
R
r0 на главный вектор системы:
n |
R |
R R |
n |
R |
R |
R |
∑(r0 |
× Fi ) = r0 |
× ∑Fi |
= r0 |
×R , |
||
i=1 |
|
|
i=1 |
|
|
|
а второе слагаемое равно главному моменту системы относительно старого центра приведения A:
∑n (R × R ) = R
ri Fi MA.
i=1
Врезультате получаем, что при перемене центра приведения главный момент
меняется по закону
R |
×R. |
MB = MA + r0 |
(5.14)
R
F1
R
F2
B
R |
|
|
r0 |
|
|
|
|
R |
|
A |
ri′ |
R |
|
R |
|
Fi |
|
Fn |
R |
|
ri |
|
|
|
|

41
Рис.5.5
Выводы:
1. Если для некоторого центра Aглавный вектор системы равен нулю (R = 0 ), то главный момент для всех точек пространства будет одинаков, поскольку MB = MA. в
соответствии с формулой (5.14).
2. Если для некоторого центра A главный момент и главный вектор системы рав-
ны нулю (MA = 0 и R = 0 ), то главный момент будет равен нулю и относительно лю-
бого другого центра.
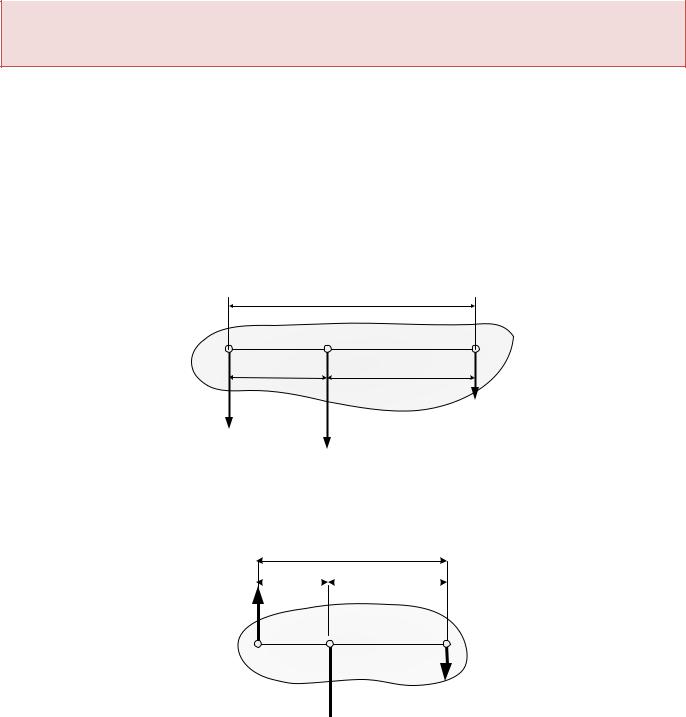
5.7.МОМЕНТЫ СИЛ, РАСПОЛОЖЕННЫХ В ОДНОЙ ПЛОСКОСТИ
Плоской системой называется система сил, линии действия которых лежат в одной плоскости.
При расположении всех сил системы на одной плоскости вектора моментов сил системы относительно точек плоскости расположены к этой плоскости перпендикулярно. Для указания их направления достаточно одного знака − знака проекции вектора на ось z, перепендикулярную к плоскости.
|
ось z |
|
|
|
R |
R |
|
|
M B (F1 ) |
||
|
R |
R |
|
R |
M B (F2 ) |
||
F1 |
|||
h1 |
|
||
|
|
||
|
B |
|
|
|
h2 |
|
|
|
R |
|
|
|
F2 |
|
|
Рис. 5.6
По этой причине при рассмотрении плоских систем под моментом силы относительно точки на самом деле понимают скалярную величину: момент силы относительно оси z, проходящей через моментную точку перпендикулярно к плоскости действия сил.
|
R |
R |
То есть |
MB (F ) = MZ (F ) |
|
Величина момента равна произведению силы на плечо:
( R ) = ± .
MB F Fh
42
Еслимомент направлен против часовой стрелки − он считается положительным.При переходе к векторному представлению такое правило знаков соответствует знаку проекции вектор-момента на ось z.
Тема 6.
ТЕОРИЯ ПАР
6.1. СЛОЖЕНИЕ ДВУХ ПАРАЛЛЕЛЬНЫХ СИЛ
До сих пор мы изучили лишь вопрос о сложении сходящихся сил. Перейдем теперь к определению равнодействующей системы параллельных
сил, остановившись сначала на случае двух параллельных сил, приложенных в точках А и В.
Здесь возможны два варианта:
1)силы направлены в одну сторону (рис. 6.1).
l
A |
C |
B |
|
l1 |
l |
|
|
2 |
|
|
R |
R |
|
F2 |
F1
R
R
Рис. 6.1
2) силы направлены в противоположныестороны и не равны по моду-
лю (рис. 6.2). Для определенности пусть F1 > F2
l2
l |
|
l1 |
F2
B |
A |
C |
R
R
 F1
F1
Рис. 6.2
43
В обоих случаях величину равнодействующей и положение линии ее действия можно найти с помощью следующей теоремы:
Равнодействующая двух параллельных сил равна их главному вектору. Линия ее действия расположена в плоскости сил, и проходит параллельно линиям действия сил на расстояниях от них, которые обратно пропорциональны модулям сил.
То есть: |
R = F1 + F2 , |
В первом случае модуль равнодействующей равен
R = F1 + F2 ,
а во втором случае R = F1 − F2 , причем равнодействующая направлена в сторону большей силы.
Линия действия равнодействующей проходит через точку С, которая в первом случае расположена в пределах отрезка АВ, а во втором случае, − за его пределами со стороны большей силы.
Отрезки, определяющие положение точки С, в обоих случаях определяются с помощью пропорций:
|
|
l1 |
= |
l2 |
= |
l |
, |
|
|
|
|
|
|
||||
|
|
F2 |
|
F1 |
|
R |
||
гдеl1, l2 |
− расстояния от линии действия равнодействующей R до линий действия |
|||||||
сил F1 |
и F2 соответственно, а |
l − |
расстояние между линиями действтя сил F1 и |
|||||
F2 . |
|
|
|
|
|
|
|
|
Следствия из теоремы:
1.Любую силу можно разложить на две параллельные силы, направленные в одну или в разные стороны. Это можно сделать бесконечным количеством способов.
R R
2. Легко заметить, что модули моментов сил F1 и F2 относительно точки С оди-
наковы, а сумма моментов будет равна нулю: ( R )+ ( R )=
MC F1 MC F2 0
3.Если система параллельных сил состоит более чем из двух сил, то, последовательно попарно суммируя эти силы, можно найти ее равнодействующую (при условии, что она существует).
6.2. ПАРА СИЛ, МОМЕНТ ПАРЫ СИЛ
44
В предыдущем параграфе, суммируя параллельные противоположно направ-
ленные силы, мы вводили существенное условие: F2 ¹ F1 .
При F2 = F1 , F2 = −F1 имеет место особый случай.
Главный вектор такой системы по модулю равен нулю.
Если бы ее равнодействующая по модулю тоже была равна нулю, то система находилась бы в равновесии. Однако, эта система в равновесии не находится, что следует из аксиомы 1.
Вывод:
система двух равных по модулю, параллельных и противоположно направленных сил равнодействующей не имеет.
Поэтому свойства таких систем сил должны изучаться отдельно.
Парой сил (или просто парой) называется система из двух равных по модулю, противоположно направленных параллельных сил.
Система сил, образующих пару, не является уравновешенной. Пара сил не имеет равнодействующей, и по этой причине ее нельзя уравновесить одной силой.
Пара есть особыйвид механического взаимодействия.
Сила и пара сил представляют собой два базовых неупрощаемых элемента статики
R ( R R ′)
m F , F
R
F ′
A
B
R
F
h
Рис. 6.3
|
|
R |
R |
′ (рис. 6.3). |
Рассмотрим пару, состоящую из сил F |
и F |
|||
|
R |
R |
|
|
Для них выполняется условие F |
′ = −F и, следовательно, главный вектор этих |
|||
сил равен нулю: |
R R |
|
|
|
F′+F = 0 |
|
|
|
|
45
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.Расстояние между линиями действия сил пары h называется плечом пары.
( R R¢)
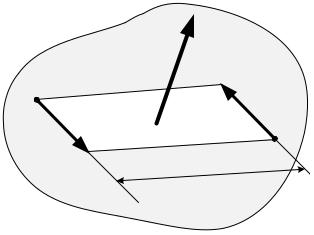
Введем теперь понятие момента пары:моментом пары F, F называется
R ( R R¢)
вектор m F, F , направленный перпендикулярно плоскости действия пары в
соответствии с правилом «правого винта»(рис. 6.3), и равный по величине про-
изведению модуля силы на плечо пары:
R R |
|
m(F, F¢)= F ×h = F¢×h |
(6.1) |
Размерность модуля момента пары [m] = Нм.
Очевидно, что модуль момента пары равен площади параллелограмма, построенного на силах пары.
6.3. СУММА МОМЕНТОВ СИЛ ПАРЫ
ТЕОРЕМА
Сумма моментов сил, составляющих пару, одинакова относительно любой точки пространства и всегда равна моменту пары.
Доказательство
Рассмотрим сумму моментов сил F и F ′ относительно произвольной точки пространстваО (рис. 6.4).
R |
= AB, |
R |
=OA, |
R |
=OB., и используя |
Преобразуем ее, введя обозначения r |
rA |
rB |
определение момента силы и условие F ′ = −F .
R R R R |
R |
R |
R |
R |
R |
R |
R |
R |
R R R |
R |
R |
MO (F )+ MO (F |
¢)= rA |
´ F |
+ rB |
´ F |
¢ = rA |
´ F |
- rB |
´ F |
= (rA - rB )´ F |
= r |
´ F |
Полученный вектор действительно не зависит от выбора точки О.

46
 O
O
R |
R |
R |
|
|
, F2 ) |
|
|
m (F1 |
R |
||
|
|
|
rB |
|
|
π 2 |
R |
|
|
rA |
|
|
|
π 2 |
|
R |
′ |
B |
|
F |
h |
||
|
|
R |
|
|
|
r |
|
R
F
A 
Рис. 6.4
Видно, что этот вектор направлен так же, как и момент пары, а по величине равен модулю момента пары:
|
R |
R |
= |
R |
F |
|
R R |
¢) |
|
r |
´ F |
r |
×sinα = Fh = m(F, F |
||||
Таким образом |
|
|
|
|||||
|
R |
R R |
R |
R R R |
|
|||
|
MO (F ) + MO (F¢) = m(F, F¢) |
(6.2) |
||||||
|
|
|
|
|
|
|
|
|
Следствие
Если в качестве центраО последовательно выбрать точкуА илиВ, то можно получить, что
R |
R |
R |
R |
R |
R |
R |
R |
R |
m(F, F¢) = M A (F¢)+ M A (F ) = M A (F¢) , |
||||||||
R |
R |
R |
R |
R |
R |
R |
R |
R |
m(F, F¢) = MB (F )+ MB (F¢) = MB (F ) .
то есть
момент пары сил равен моменту одной из сил пары относительно точки приложения другой силы пары.
6.4. ТЕОРЕМА ОБ УСЛОВИЯХ ЭКВИВАЛЕНТНОСТИ ПАР
ТЕОРЕМА
Две пары, имеющие векторно-равные моменты, эквивалентны друг дру-
гу.
Справедливость этой теоремы равносильна справедливости следующих трех
47
утверждений (трех более простых теорем).
1.Можно сделать любыми величины сил и плеча пары, сохраняя их произведение, т. е. модуль момента пары.
2.Пару можно переносить в любое другое положение в плоскости ее действия и поворачивать ее на произвольный угол.
3.Пару можно переносить на параллельную плоскость действия.
Приведем доказательство этих утверждений.
1-е утверждение (Теорема об изменении плеча и силы пары)
Можно сделать любыми величины модулей сил и плеча пары, сохраняя их произведение, т. е. модуль момента пары.
|
|
R′ |
|
|
|
|
R |
||
|
|
|
|
|
|
F ′ |
|||
F = F ′ |
F |
|
F = F ′ |
R |
1 |
|
|||
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
2 |
F ′ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
A |
C |
A′ |
|
|
A |
|
C |
A′ |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
F1 |
a |
a |
|
h = 2a
|
|
R |
R |
|
F2 |
|
||
|
|
|
F1 |
a |
a |
|
h = 2a
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
|
P′ |
P = P′ = F1 + F2 |
|
P′ |
|
|
|
|
|
|
|
|
|
|
|
||
A |
B |
C |
B′ |
A′ |
B |
C |
B′ |
|
R |
|
|
|
|
|
|
|
P |
|
|
|
R |
|
|
|
|
|
|
|
P |
|
|
a1 |
a2 |
|
a2 |
a1 |
a2 |
|
a |
|
|
|
|
|
|
|
2 |
|
a |
|
a |
|
|
d = 2a2 |
|
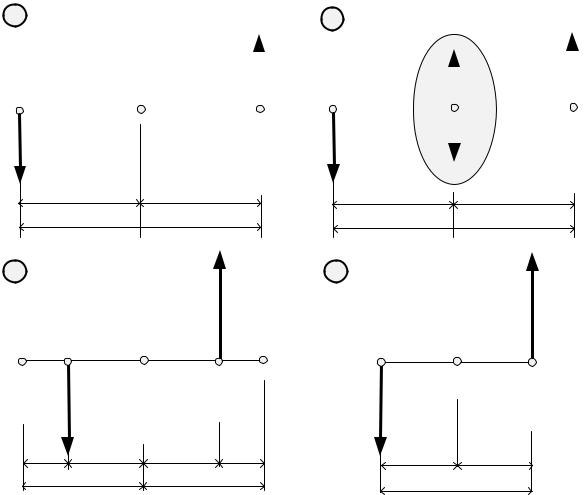
Рис. 6.6
Доказательство
48
∙ Пусть в точках A и A′ к твердому телу приложены равные по модулю (F1 = F1′= F ) силы, образующие пару с плечом h = 2a (рис.6.6, а). Момент этой
( R R′)
пары равен m F1, F1 = F1h;
∙Приложим в точке С (середина отрезка AA′) (рис.6.6, б) систему произвольных по величине сил:
|
R R |
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
|
||
|
(F2 , F2¢ )≡ 0 , которая уравновешена, так как |
F2¢ = -F2 |
|
|||||||||||||||
∙ |
|
|
|
|
|
|
|
|
|
R |
R |
R |
R |
R |
R |
, |
||
Сложив параллельные силы P = |
F |
+ F ¢, |
P |
= F |
+ F ¢ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
|
||
|
получим |
пару сил (P, P′), приложенных в точках B и B′ (рис. 6.6, в), поло- |
||||||||||||||||
|
жение которых определяется пропорцией: |
|
|
|
||||||||||||||
|
|
a1 |
= |
a2 |
= |
a |
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
F2 |
|
F1 |
|
P |
|
|
|
|
|
|
|
|
|
|||
|
из которой следует, что |
|
|
|
|
|
|
|
|
|
||||||||
|
|
a2 P = aF1 |
|
|
и далее, что |
|
a2 = |
a F1 |
|
|
|
|
||||||
|
|
|
|
|
P |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
R R |
|
|
|
|
|
|
|
||
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Момент пары сил (P, P′) |
будет равен |
|
|
|
|
|
||||||||||||
|
|
|
R |
|
R |
|
|
|
|
aF1 |
|
|
|
|
|
R |
R |
|
|
m (P, P¢) |
= Pd = P × 2a2 |
= P × 2 |
= 2aF1 = Fh = m (F1 , F1¢). |
||||||||||||||
|
P |
|||||||||||||||||
|
|
|
R |
|
R |
|
|
R R |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
m(P, P′) |
= m(F1, F1′) |
|
|
|
|
|
|
|
|
|
|||||||
Первое утверждение доказано.
2-е утверждение (Теорема о повороте сил пары в ее плоскости)
Пару можно переносить в любое другое положение в плоскости ее действия (в пределах данного тела).
Доказательство
∙ |
Проведем две параллельные прямые I и II , расположенные на расстоянии d друг |
|
|
от друга. Под углом к ним проведем еще две такие же прямые I ′ и II′. |
|
∙ |
R |
R |
Пусть на прямых I и II лежат силы F1 и |
F2 F1 = F2 = F , образующие пару |
|
(рис.6.7), алгебраический момент которой равен ( R R )= . m F1, F2 Fd

49
|
|
|
|
|
|
R |
|
|
|
|
|
R |
|
d |
|
|
F2 |
|
|
d |
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
F1 |
|
|
|
π 2 |
|
|
|
|
|
|
II ′ |
|
|
|
|
|
II ′ |
|
|
|
|
|
|
|
|
R |
R |
|
|
R |
R |
|
|
|
|
|
F2 |
|
|
F2 |
||
I ′ |
|
|
|
|
P2 |
I ′ |
|
P2 |
||
|
π 2 |
|
|
|
π 2 |
R |
||||
|
|
|
|
|
|
R2 |
||||
|
|
|
|
|
R |
R |
|
|||
|
|
|
|
|
|
|
|
R |
||
|
R |
|
|
|
|
P′ |
P′ |
|
|
|
|
P′ |
|
d |
|
|
2 |
1 |
|
d |
P2′ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
d |
|
|
R |
|
d |
P2 |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π 2 |
R1 |
|
|
|
|
|
F |
R |
π |
2 |
|
R |
π 2 |
π 2 |
||
|
1 |
|
|
|
||||||
|
|
P |
|
|
|
|
R |
P |
|
|
|
|
1 |
|
|
|
|
F1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
d |
|
I |
|
|
|
II |
|
I |
|
II |
|
|
|
|
|
|
|
|
|
|
|
|
R
P
1
Рис. 6.7.
∙Перенесем силы F1 и
∙По направлениям I ′R
R
F2 вдоль линий их действия I и II в точки А и В.
и II′ приложим две уравновешенные системы сил, которые
RR
равны по модулю силам |
F1 |
и F2 : |
1 |
1 |
|||
|
( 1 |
1 ) |
|
|
|
||
|
R |
R |
|
|
|
R |
R |
|
P , P′ ≡ 0 , так как |
|
P′ = −P |
||||
|
R |
R |
|
|
|
R |
R |
и |
(P2 , P2′) ≡ 0 , так как, |
P2′ = −P2 |
|||||
причем P = P = P′ = P′ = F = F = F . |
|||||||
|
1 |
2 |
1 |
2 |
1 |
|
2 |
∙Сложим силы по правилу параллелограмма (в данном случае параллелограмм имеет форму ромба):
R′ |
R |
R |
R′ |
R |
R |
P |
+ F |
= R , |
P |
+ F |
= R . |
1 |
1 |
1 |
2 |
2 |
2 |
∙Полученные силы R1 и R2 равны, противоположно направлены R1 = −R2 , лежат на одной прямой и, следовательно, по I аксиоме образуют уравновешенную систе-RRR R
му, которая может быть исключена.
∙ |
|
R |
R |
образуют систему, которая эквивалентна заданной си- |
Оставшиеся силы |
P |
и P |
||
|
|
1 |
2 |
|
RR
стеме сил F1 и F2 . Убедимся, что момент пары в результате проделанных эквивалентных преобразований не изменился:
