
8781
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
В.Г. Лапин, А.А. Краснов, В.Б. Штенберг
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ФИЗИКЕ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине
«Физика» для обучающихся по направлению подготовки 27.03.01 Стандартизация и
метрология. Профиль Стандартизация и сертификация.
Нижний Новгород ННГАСУ
2016
2
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
В.Г. Лапин, А.А. Краснов, В.Б. Штенберг
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ФИЗИКЕ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине
«Физика» для обучающихся по направлению подготовки 27.03.01 Стандартизация и
метрология. Профиль Стандартизация и сертификация.
Нижний Новгород
2016
3
УДК 53(075)
Лапин В.Г.. Физика[Электронный ресурс]: учеб.- метод. пос. / А.А. Краснов, В.Б. Штенберг; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2016. – 212 с; 108 ил. 1 электрон. опт. диск (CD-R)
Методические указания содержат основные теоретические положения по общему курсу «Физика» для самостоятельной работы студентов.
Пособие для самостоятельной работы студентов по общему курсу физики состоят из пяти частей: «Механика», «Термодинамика и молекулярная физика», «Электричество и магнетизм», «Колебания и волны», «Квантовые явления». В каждой части кратко описываются основные законы, в конце имеется сводка основных соотношений, вопросы для самопроверки и примеры решения задач. Вопросы, которые можно опустить при первичном прочтении отмечены одной звёздочкой (*), а вопросы, имеющие факультативный характер двумя звёздочками (**).
Предназначено обучающимся в ННГАСУ для подготовки к лекционным практическим занятиям по направлению подготовки 27.03.01 Стандартизация и метрология.
Профиль Стандартизация и сертификация.
© В.Г. Лапин, А.А. Краснов, В.Б. Штенберг,2016 © ННГАСУ, 2016.
4
Часть 1 Механика
Введение
Механика — часть физики, которая изучает простейшую и наиболее общую форму движения материи, заключающуюся в перемещении тел или частей тела относительно друг друга и называемую механическим движением.
Развитие механики как науки начинается с III в. до н. э., когда древнегреческий ученый Архимед сформулировал закон равновесия рычага (на нем основано устройство всех машин) и законы равновесия плавающих тел. Основные законы механики в значительной мере выяснены итальянским физиком и астрономом Г.Галилеем и окончательно сформулированы английским ученым И.Ньютоном.
Механика Галилея — Ньютона называется классической и изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью света, изучаются теорией относительности, сформулированной А.Эйнштейном. Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики не применимы — они изучаются квантовой механикой.
Механика подразделяется на три раздела: кинематику; динамику; статику. Кинематика изучает движение тел, не рассматривая те причины, которые
это движение обусловливают.
Динамика изучает законы движения тел и те причины, которые вызывают или изменяют это движение.
Статика изучает законы равновесия системы тел.
Глава 1. Кинематика
§ 1. Система отсчета. Траектория материальной точки
Наиболее простым примером механического движения является движение материальной точки. Материальная точка — это тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное понятие, но его введение облегчает решение конкретных задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки. Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное место. Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. Выбранное таким образом тело условно считается неподвижным, а связанная с

5
|
|
ним произвольная |
система |
координат |
|
Z |
A |
называется |
системой |
отсчета |
положений |
|
|
материальной точки. В декартовой системе |
|||
|
r |
координат, |
используемой наиболее часто, |
||
|
z |
положение точки А в данный момент времени |
|||
|
|
||||
0 |
y X |
по отношению к этой системе характеризуется |
|||
|
тремя координатами x, у и z или радиусом- |
||||
Y |
x |
вектором r, проведенным из начала отсчета в |
|||
|
данную точку (рис. 1). |
|
|
||
|
|
|
|
||
|
Рис.1 |
При движении материальной точки ее |
|||
|
координаты с течением времени изменяются. |
||||
|
|
||||
|
|
В общем случае ее движение определяется |
|||
|
|
тремя скалярными уравнениями: |
|
||
x = x (t), |
|
|
(1.1) |
y = y (t), |
|
|
|
z = z (t), |
|
эквивалентными векторному уравнению:
|
|
|
r = r (t). |
|
|
(1.2) |
|
Z |
|
S |
Число |
независимых |
координат, |
||
A |
B |
полностью определяющих положение точки в |
|||||
|
|||||||
|
|
r |
пространстве, называется числом степеней |
||||
|
r0 |
r |
свободы. Если материальная точка движется в |
||||
|
пространстве, то, как уже было сказано, она |
||||||
0 |
|
|
|||||
|
X |
обладает |
тремя |
степенями |
свободы |
||
|
|
(координаты х, у и z), если по некоторой |
|||||
Y |
|
|
поверхности, то двумя степенями свободы, |
||||
|
|
|
если по кривой, то одной степенью свободы. |
||||
|
Рис.2 |
Исключая t в уравнениях (1.1) и (1.2), |
|||||
|
|
|
получим уравнение |
траектории |
движения |
||
|
|
|
материальной точки. |
Траектория |
движения |
||
материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или
криволинейным.
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной
точкой с момента начала отсчета времени, называется длиной пути |
s и |
является скалярной функцией времени: s = s (t). Вектор Δг = г — |
г0, |
проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется перемещением.

|
6 |
Естественно, что при прямолинейном движении вектор перемещения |
|
совпадает с соответствующим |
участком траектории и модуль перемещения |
| Δг | равен пройденному пути |
s. |
§ 2. Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость, которая определяет как быстроту движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0 (рис. 3). В течение небольшого промежутка времени t точка пройдет путь s и получит элементарное перемещение r.
Величина
|
|
v |
= |
r |
|
|
|
|
|
(2.1) |
|
|
|
t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
называется средней скоростью движения за время |
t. |
Направление средней |
|||||||||
|
|
скорости совпадает с направлением Δг. |
|||||||||
|
v |
Если |
в (2.1) |
перейти |
к пределу |
при |
|||||
|
Δг → 0, то получим |
выражение |
для |
||||||||
|
s |
мгновенной скорости v: |
|
|
|
|
|
||||
A |
<v> |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
r = |
dr |
|
|
|
||
|
r |
|
|
v = lim |
|
|
|
||||
|
|
|
dt |
|
|
||||||
|
|
|
|
|
r→0 t |
|
|
|
|||
r0 |
|
|
Мгновенная |
скорость |
v |
есть |
|||||
0 |
|
векторная |
величина, |
равная |
первой |
||||||
Рис. 3 |
производной |
|
|
радиуса-вектора |
|||||||
|
|
|
|||||||||
|
|
движущейся точки по времени. Так как |
|||||||||
|
|
секущая |
в |
пределе |
|
совпадает |
с |
||||
касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3).
По мере уменьшения t путь |
s все больше будет приближаться к | r |, |
||||||||||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
= lim |
| |
r | |
= lim |
s = |
ds |
|
|
υ =| v |= |
lim |
|
|||||||||
t |
|
|
|
t |
|
||||||
|
r→0 |
|
|
r→0 |
r→0 |
t dt |
|||||
Таким образом, числовое значение мгновенной скорости равно первой производной пути по времени:
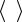
7 |
|
|
|
υ = lim |
s = |
ds |
(2.2) |
|
|||
r→0 |
t dt |
|
|
В случае неравномерного движения, когда числовое значение мгновенной скорости с течением времени изменяется, пользуются скалярной величиной <v> – средней скоростью неравномерного движения на данном участке:
υ = |
s |
|
t |
||
|
Из рис. 3 вытекает, что <v> > | <v> |, так как s > | Δг | и только в случае прямолинейного движения
s = | Δг |
Если выражение ds = υ dt (см. формулу (2.2)) проинтегрировать по временив пределах от t до t + t, то найдем длину пути, пройденного точкой за время t:
t + t |
|
s = ∫ υ dt |
(2.3) |
t
В случае равномерного движения, когда числовое значение мгновенной скорости постоянно, выражение (2.3) примет вид
t + t
s = υ ∫ dt = υ t
t
Путь, пройденный точкой за промежуток времени от t1 до t2, дается интегралом
t 2
s = ∫ υ(t) dt
t1
§3. Ускорение и его составляющие
Вслучае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Пусть вектор v задает скорость точки А в момент времени t. За время t движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению, равную v1 = v + v. Перенесем вектор v1 в
точку А и найдем v (рис. 4).

8
Средним ускорением неравномерного
v C |
vτ |
D |
движения в интервале от t до t + |
t |
|||||
|
|||||||||
s |
называется векторная величина, равная |
||||||||
A |
B |
||||||||
|
|
|
отношению изменения скорости |
v к |
|||||
|
|
E |
интервалу времени |
|
t: |
|
|||
|
|
|
|
|
v |
|
|
||
vn |
v |
v1 |
a |
= |
|
|
|||
|
|
t |
|
||||||
|
|
|
|
|
|
|
|||
0
Рис. 4
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
a = lim a |
= lim |
v |
= |
dv |
(3.1) |
|
|
||||
t→0 |
t→0 |
t dt |
|
||
Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.
Разложим вектор v на две составляющие. Для этого из точки А (см. рис. 4) по направлению скорости v отложим вектор AD, по модулю равный
v1. |
Очевидно, что вектор |
CD, |
равный |
vτ, представляет собой изменение |
скорости по модулю за время t: Δυτ = υ1 — |
υ. Вторая же составляющая вектора |
|||
v— |
vn характеризует изменение скорости за время t по направлению. |
|||
|
Предел отношения |
υτ , |
являющийся производной от скорости по |
|
|
|
t |
|
|
времени, определяет быстроту изменения скорости в данный момент времени t
и является тангенциальной составляющей ускорения |
aτ: |
||||||||
a |
τ |
= lim |
υτ = lim |
υ = |
dυ |
|
(3.2) |
||
|
|||||||||
|
t→0 |
t |
t→0 |
t |
|
dt |
|
||
|
|
|
|
||||||
Определим вторую составляющую ускорения. Допустим, что точка В |
|||||||||
достаточно близка к точке А, |
поэтому |
s |
можно считать дугой окружности |
||||||
некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия
треугольников АОВ и EAD следует vn/АВ = υ1/r, но так как АВ = υ |
t, то |
||||||||
|
|
|
|
|
υn = υυ1 |
|
|
|
|
|
|
|
|
|
t |
к |
|
|
|
В пределе при |
t → 0 |
v1 → v. |
|
|
|
|
|
||
Поскольку v1 → v, угол EAD стремится к нулю, а так как треугольник |
|||||||||
EAD равнобедренный, то угол ADE между v |
и |
vn, стремится к прямому. |
|||||||
Следовательно, |
при |
t |
→ |
0 |
векторы |
vn |
и |
v оказываются |
взаимно |
перпендикулярными. |
Так |
как |
вектор скорости |
направлен по касательной к |
|||||

9
траектории, то вектор vn, перпендикулярный скорости, будет направлен к центру круга ее кривизны. Вторая составляющая ускорения, равная
a |
n |
= lim |
υn |
= υ2 |
, |
(3.3) |
|
t→0 |
t |
r |
|
|
|
|
|
|
|
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также
).
геометрическая сумма тангенциальной и
v |
a = |
dv |
= a τ + an |
(3.4) |
|
aτ |
dt |
||||
|
|
|
|||
|
|
|
|
|
a |
Итак, |
тангенциальная |
составляющая |
||
|
ускорения |
характеризует |
быстроту |
изменения |
||
|
|
|||||
an |
|
скорости по модулю (направлена по касательной |
||||
|
к траектории), а нормальная составляющая |
|||||
|
|
|||||
|
|
ускорения |
характеризует |
быстроту |
изменения |
|
Рис. 5 |
|
скорости по направлению (направлена к центру |
||||
|
кривизны траектории). С учетом тангенциальной |
|||||
|
|
|||||
инормальной составляющих ускорения
движение можно классифицировать следующим образом:
1)аτ = 0, аn = 0 — прямолинейное равномерное движение;
2)аτ = а = const, an = 0 — прямолинейное равнопеременное движение. При таком виде движения
a τ |
= a = |
υ |
= |
υ2 |
− υ1 |
|
t |
t 2 |
− t1 |
||||
|
|
|
Если начальный момент времени t1 = 0, а начальная скорость υ1 = υ0, то, обозначив t2 = t и υ2 = υ, получим a = (υ – υ0)/t, откуда
υ = υ0 + at
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, получим формулу для пройденного пути в случае равнопеременного движения:
t |
t |
s = ∫ υ dt = ∫(υ0 + at)dt = υ0 t + at 2 / 2 ;
0 |
0 |

10
3)аτ = f (t), аn = 0 — прямолинейное движение с переменным ускорением;
4)аτ = 0, аn= const. При аτ = 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы аn= υ2/r следует, что радиус кривизны должен быть постоянным. Следовательно, имеем дело с равномерным движением по окружности;
5)аτ =0, аn = f (t) — равномерное криволинейное движение;
6)аτ =const, аn ≠ 0 — криволинейное равнопеременное движение;
7)аτ = f (t), аn ≠ 0 — криволинейное движение с переменным ускорением.
§4. Угловая скорость и угловое ускорение
Вслучае движения материальной точки по
Δφ
R s
Рис. 6
окружности по аналогии с линейными скоростью и ускорением вводятся угловая скорость и угловое
ускорение.
Пусть точка движется по окружности радиуса R (рис. 6). Ее положение через малый промежуток времени зададим углом Δφ. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
ω = lim |
ϕ |
= |
dϕ |
(4.1) |
|
|
|||
t →0 |
t dt |
|
||
Направление вектора угловой скорости задается правилом винта: вектор угловой скорости совпадает по направлению с поступательным движением острия винта, головка которого вращается в направлении движения точки по окружности (рис. 7). Размерность угловой скорости [ω] =Т -1, а ее единица — радиан в секунду (рад/с).
ω |
Линейная скорость точки (см. рис. 6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
υ = lim |
s = lim |
R |
ϕ |
= R lim |
ϕ = |
ds |
= Rω |
|
|
|
|
|
||||||
|
t→0 |
t t→0 |
t |
t→0 |
t dt |
||||
|
т. е. |
|
|
|
|
|
|
|
|
0 R |
v |
|
|
υ= ωR. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если ω = const, то вращение равномерное и его
Рис. 7 |
можно характеризовать периодом вращения Т — |
|
временем, за которое точка совершает один полный |
||
|
||
|
оборот, т. е. поворачивается на угол 2π. Так как |
|
|
промежутку времени t = Т соответствует Δφ = 2π, |
|
то |
|
|
|
ω = 2 π /Т. |
