
8777
.pdf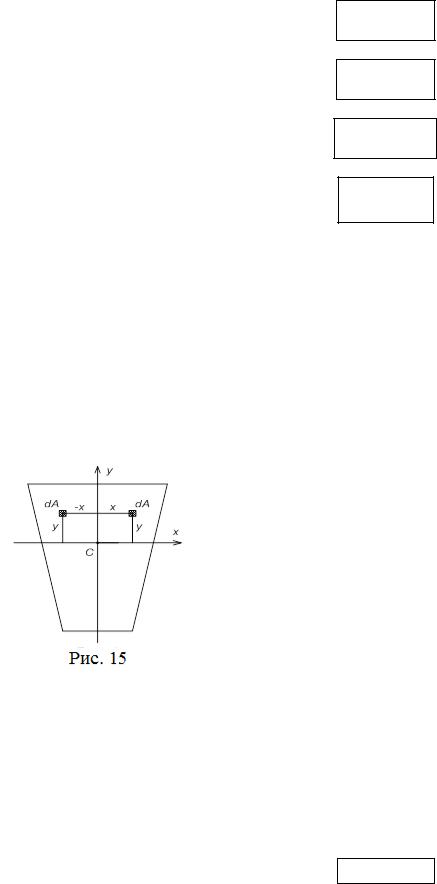
Для плоского поперечного сечения можно ввести следующие новые геометрические характеристики:
осевой момент инерции сечения относительно оси х:
Jx = ∫y 2 dA ;
A
осевой момент инерции сечения относительно оси у:
Jy = ∫x 2 dA ;
A
центробежный момент инерции сечения:
Jxy = ∫xy dA ;
A
полярный момент инерции сечения:
Jp = ∫ρ2 dA .
Для моментов инерции можно указать следующие свойства:
моменты инерции имеют размерность мм4, см4 и т. д.;
осевые моменты инерции Jx, Jy и полярный момент инерции Jpвсегда положительны и
не равны нулю;
центробежный момент инерции Jxy может быть положительным, отрицательным и равным нулю;
оси, относительно которых центробежный момент инерции равен нулю: J xy = 0, в
дальнейшем будем называть главными осями инерции.
Рассмотрим сечение, у которого ось у, например, - ось симметрии
(рис.15).
Центробежный момент инерции двух площадок, расположенных симметрично, равен:
dJxy = xydA – xydA = 0.
Интегрируя по площади сечения, имеем J xy = 0.
Таким образом, центробежный момент инерции сечения
относительно осей, из которых одна или обе являются осями симметрии, равен нулю.
Складывая осевые моменты инерции и учитывая, что ρ 2 = х2 + у2 , получим
Jx + Jy = ∫y 2 dA + ∫x 2 dA = ∫(x 2 + y 2 )dA = ∫ρ2 dA = Jp ,
A A A A
т.е. сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей:
Jx + Jy = J ρ .
Осевой момент инерции сложного сечения относительно некоторой оси равен сумме осевых моментов инерции составляющих его частей относительно этой же оси.
Аналогично, центробежный момент инерции сечения относительно двух взаимно перпендикулярных осей равен сумме центробежных моментов инерции составляющих его
частей относительно этих же осей.
Полярный момент инерции сложного сечения относительно некоторой точки равен сумме полярных моментов инерции составляющих его частей относительно этой же точки.
Следует помнить, что нельзя суммировать моменты инерции, вычисленные относительно различных осей и точек.
3. Моменты инерции простейших сечений.
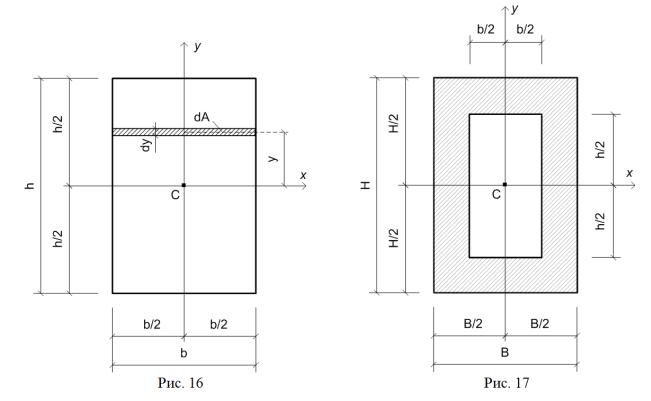
1). Осевые моменты инерции прямоугольного сечения шириной b и высотой h относительно осей симметрии прямоугольника х и у (рис. 16).
Выделим линиями, параллельными оси х, элементарную полоску высотой dy и
шириной b. Площадь этой полоски dA = bdy, а координата её центра тяжести – у. Пределы интегрирования: от y = - h/2 до y = + h/2. Вычислим осевой момент инерции прямоугольника относительно оси симметрии х:
|
|
h / 2 |
b h |
3 |
|
|
Jx |
= ∫y 2 dA = b ∫y 2 dy = |
|
. |
|||
12 |
||||||
|
A |
−h / 2 |
|
|||
|
|
|
|
|||
Аналогично, Jy = |
h b 3 |
. Оси х и у – |
оси симметрии фигуры, поэтому Jxy = 0. |
||||||
|
|
||||||||
12 |
|
|
|
|
|
|
|
||
Для квадратного сечения h = b = a и |
Jx = Jy = |
a 4 |
. |
|
|||||
|
|||||||||
|
|
|
|
|
12 |
|
|
||
Для прямоугольного коробчатого сечения (рис. 17) моменты инерции равны разности |
|||||||||
моментов инерции большого прямоугольника и малого прямоугольника: |
|||||||||
Jx = |
B H 3 − b h 3 |
; Jy = |
H B 3 − h b 3 |
; Jxy = 0 . |
|||||
|
|
||||||||
|
|
|
12 |
|
12 |
|
|
||
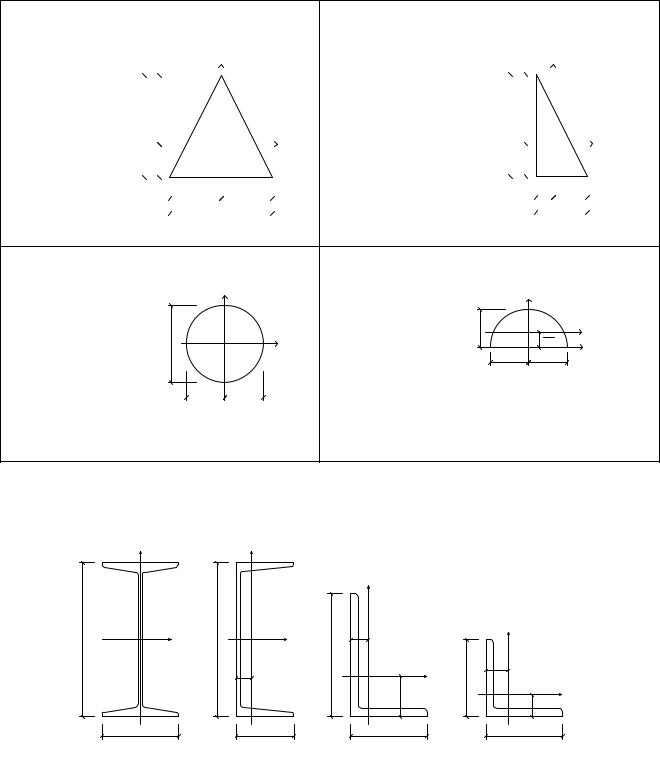
2). Равнобедренный треугольник |
3). Прямоугольный треугольник |
||||||||||||||||||||||||||
Jx |
= |
b h 3 |
; |
|
|
|
|
|
|
|
|
|
Jx |
= |
|
b h 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
36 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
||||
|
= |
h b 3 |
|
|
|
|
Jy |
= |
h b 3 |
|
|
|
|
|
|
|
|
|
|||||||||
Jy |
|
|
|||||||||||||||||||||||||
48 |
; |
|
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Jxy |
= ± |
b 2 h 2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Jxy = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4). Круг |
|
|
5). Полукруг |
|
||
Jx |
= |
π d |
4 |
J x1 |
= π d 4 ; |
|
64 |
; |
|
128 |
4r |
||
|
|
|
|
= π d 4 |
3 π |
|
Jy |
= |
π d |
4 |
J y |
; |
|
|
; |
|
128 |
|
||
|
|
64 |
|
|
|
|
|
|
J |
x |
= π d 4 (1− |
64 |
) ; J |
xy |
= 0. |
|
|
|||||||
|
|
|
||||||
Jxy = 0 . |
|
|
128 |
9π 2 |
|
|||
|
|
|
|
|
||||
В строительстве широкое применение находит прокатная сталь. Сечения прокатных профилей показаны на рис. 18:
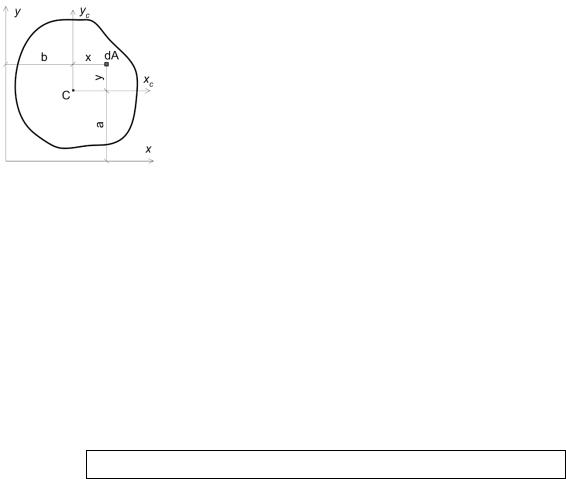
Рис. 18
Геометрические характеристики прокатных профилей определяют из таблиц на
прокатную сталь.
4. Преобразование моментов инерции при параллельном переносе осей.
|
Установим зависимость между моментами инерции одного и того же сечения |
|||
относительно разных, но параллельных осей. |
|
|||
|
|
Предположим, |
что моменты инерции сечения относительно её |
|
|
|
центральных осей J xc , J yc |
, J xc yc известны (рис. 19). |
|
|
|
Необходимо определить |
моменты инерциии сечения относительно |
|
|
|
произвольных осей х и у, параллельных центрральным осям хси ус этого |
||
|
|
сечения. |
|
|
Используя обозначения |
Рис. 19 |
рисунка 19, вычислим осевой момент |
||
|
|
относительно оси х. |
||
инерции сечения |
|
|||
J x = ∫ ( y + а) 2 dA = ∫ y 2 dA + 2 a ∫ y dA + a 2 ∫ dA = J xc |
+ 2 a S xc + a 2 A . |
|||
A |
A |
A |
A |
|
Учитывая, что статические моменты фигур относительно центральных осей равны нулю:
Sxc = 0 , в результате получаем
Jx = Jxc + a 2 A .
Выполняя аналогичные вычисления для второго осевого моменнта инерции и центробежного момента инеерции, будем иметь следующие формулы преобразования моментов инерции при параллельном переносе осей
Jx = Jxc + a 2 A . Jy = Jyc + b 2 A . Jxy = J xc yc + a b A .
Из формул для осевых моментов инерции следует, что для всех параллельных осей наименьшее значение осевые моменты инерции имеют относительно центральных осей хси ус.
Если заданное сечение можно разбить на простейшие фигуры, то полуученные формулы вычисления моментов инер ции при параллельном переносе осей можно записать в следующем виде
J x = ∑( J xi + a i2 A i ) ; J y = ∑( J yi + b i2 A i ) ; J xy = ∑( J xi yi + a i b i A i ) .
5. Преобразование моментов инерции при повороте осей.
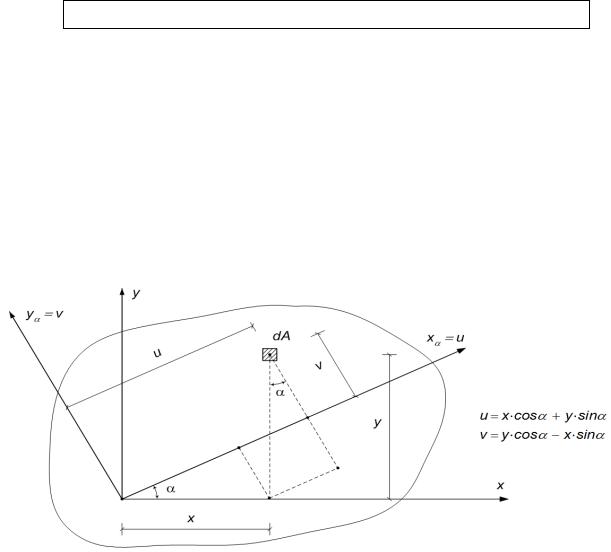
Предположим, что моменты инерции сечения Jx, Jy, Jxy относительно заданной системы координат х, у известны. Повернём заданную систему координат вокруг начала координат на произвольный угол ά (рис. 20). Положительным будем считать угол поворота от положительного значения х к положительному значению у.
На рис. 20 показан положительный угол поворота для заданной системы координат.
Формулы, связывающие координаты центра тяжести элементарной площадки dA в новой
(повёрнутой) и старой системах координат, приведены на рис. 20.
|
Рис. 20 |
6. Главные оси инерции. Главные моменты инерции. |
|
Как было установлено ранее, |
Jx + Jy = Jp . |
Если оси координат поворачивать в своей плоскости вокруг начала координат, то
полярный момент инерции останется неизменным, а осевые моменты инерции будут изменяться, причём Jx + Jy = const.
Если сумма двух переменных величин остаётся постоянной, то одна из них уменьшается, а другая увеличивается. Следовательно, при каком-то положении осей один из осевых моментов инерции достигает максимального значения Jmax, а другой момент инерции -
минимального значения Jmin.
Оси, относительно которых моменты инерции имеют максимальное и минимальное значения, называются главными осями инерции, а моменты инерции – главными моментами инерции.

В теории моментов инерции доказывается, что центробежный момент инерции равен
нулю: J xy = 0 относительно главных осей инерции.
Ранее мы установили, что центробежный момент инерции равен нулю, если одна из
осей х или у – ось симметрии. Кроме того, ось симметрии – |
центральная ось. |
|||||||||||
Следовательно, оси симметрии фигуры являются главными центральными осями |
||||||||||||
инерции. |
|
|
|
|
|
|
|
|
|
|
||
Величины главных моментов инерции можно определять по формуле |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jx + Jy |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|||
|
J max |
= |
|
± |
|
|
( Jx − Jy ) |
|
+ 4 J xy . |
|
||
2 |
2 |
|
|
|||||||||
|
|
min |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ось, относительно которой момент инерции достигает максимального значения,
называется осью максимум или первой главной осью инерции.
Ось, относительно которой момент инерции достигает минимального значения,
называется осью минимум или второй главной осью инерции.
Поскольку сумма осевых моментов инерции должна оставаться постоянной, то для проверки вычислений можно использовать равенство
Jx + Jy = Jmax + Jmin .
Углы наклона главных осей инерции относительного исходной оси х можно определять по следующим формулам
tg α max |
= |
|
J xy |
; tg α min |
= |
|
J xy |
. |
|
J y |
− Jmax |
Jy |
− Jmin |
||||||
|
|
|
|
|
Из формул следует, что, если один из углов получится положительным, то другой будет обязательно отрицательным. Для проверки вычислений можно использовать условие,
что сумма абсолютных значений углов должна быть равна девяносто градусов:
α max + α min = 90o .
7. Моменты сопротивления сечений.
При решении задач изгиба и кручения используется геометрическая характеристика сечения, которая называется моментом сопротивления.
Осевым моментом сопротивления называют отношение главного центрального момента инерции к расстоянию от главной центральной оси до самой удалённой точки на внешнем контуре сечения (рис.21):

Wx( 1) = |
|
|
J |
x |
|
; Wx( 2 ) = |
|
|
J |
x |
|
; Wy |
= |
|
Jy |
|
. |
|
|
y1 |
|
|
|
y 2 |
|
|
x3 |
|
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Моменты сопротивления вычисляются в мм3, см3 и т. д.
Моменты сопротивления величины положительные и не равны нулю.
Моменты сопротивления сложных сечений не равны сумме моментов сопротивлений
Рис. 21
составных частей сечения, за исключением некоторых фигур.
Подсчитаем моменты сопротивления прямоугольного сечения:
|
b h 3 |
|
|
b h 2 |
|
|
h b 3 |
|
|
h b 2 |
|
||||
Wx = |
12 |
|
= |
; Wy = |
|
12 |
|
= |
. |
||||||
|
|
|
|
|
|
|
|||||||||
|
|
h |
|
6 |
|
|
|
b |
|
6 |
|
||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||
Момент сопротивления коробчатого сечения относительно оси х:
|
|
B H 3 − b h 3 |
|
|
B H 2 |
|
|
||
|
= |
12 |
|
= |
− |
||||
Wx |
|
|
|
|
|
1 |
|||
|
H |
|
|
6 |
|||||
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
Осевой момент сопротивления круглого сечения:
|
π d 4 |
= π d 3 |
||
Wx = Wy = |
64 |
|||
|
||||
|
|
d |
|
32 |
|
2 |
|
|
|
b h 3 B H 3 .
.
При решении задач кручения круглых стержней используются полярный момент инерции и полярный момент сопротивления.
Полярный момент инерции круга: Jp = Jx |
+ Jy |
= |
π d 4 |
+ |
π d |
4 |
π d |
4 |
||
64 |
64 |
= |
32 |
. |
||||||
|
|
|
|
|
|
|||||
|
|
|
π d 4 |
= π d 3 . |
|
|
||||
Полярный момент сопротивления круга: |
Wp |
= |
32 |
|
|
|||||
|
|
|
||||||||
|
|
|
|
d |
|
|
16 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Лекция №3
Определение внутренних сил в стержнях
1.ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ
Силы в сопротивлении материалов принято разделять на силы, действующие на конструкцию извне (внешние
силы) и силы, возникающие в результате взаимодействия частей конструкции между собой (внутренние силы).
1.1 Активные и реактивные внешние силы
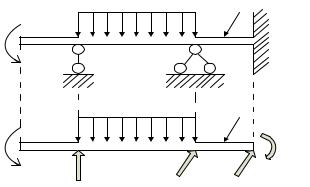
Рассмотрим тело (рис.22), у которого один размер значительно превышает два других (стержень или брус). На него действует внешняя нагрузка: q, F, М. Это активные силы.
Рис. 22
Стержень имеет опоры А, В и С (рис.22а). Силы, с которыми опоры воздействуют на брус, по отношению к нему также являются внешними. Это реакции (реактивные силы): RA ,RB, Rc, Мс (рис.22б).
1.2Система координат.
Оси х и у будем считать главными центральными осями сечения и располагать в его плоскости. Ось z в этом случае будет направлена по оси стержня (геометрическое место центров тяжести всех поперечных сечений стержня) .
1.3 Определение опорных реакций.
Для определения n опорных реакций необходимо составить n уравнений равновесия, следя за тем, чтобы уравнения были независимыми друг от друга. Для произвольной системы сил на плоскости можно составить три линейно независимых уравнения равновесия. Для системы параллельных сил - лишь два.По направлению связи возникает реакция (рис. 22).
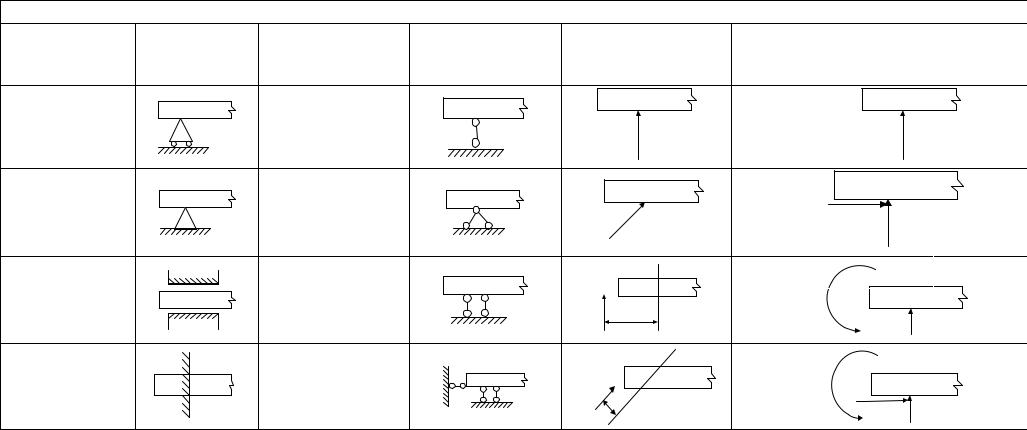
Характер и направление реакции на опоре определяется числом и расположением связей, что в свою очередь зависит от конструкции опоры (Табл. 1.1).
При составлении уравнений равновесия используют правило знаков, принятое в теоретической механике.
- 2 9 -
|
|
|
|
Таблица 1.1 |
|
Различные виды опор, используемые при построении плоских и расчетных схем |
|
||
|
Схематическое |
Число и |
Характер и |
|
|
расположение |
направление |
|
|
Название опоры |
Запрещение степени свободы |
Компоненты реакции |
||
|
изображение |
связей |
реакции |
|
|
|
|
||
Шарнирно- |
Перемещение по |
|
|
|
ПОДВИЖНАЯ |
направлению |
|
|
|
|
|
|
|
|
опора |
связи |
|
|
|
|
|
|
||
Шарнирно- |
Перемещения по двум |
|
|
|
неподвижная |
|
|
|
|
направлениям |
|
|
|
|
опора |
|
|
|
|
|
|
|
|
|
|
Перемещение по |
|
|
Ma |
Подвижная заделка |
направлению связей и |
|
|
A |
|
поворот |
|
|
Ra |
|
|
|
|
|
Жесткаязаделка |
Перемещение по двум |
|
|
|
направлениям и поворот |
|
|
|
|
|
|
|
|
|
1.4. Эпюры внутренних сил
Если взять для рассмотрения несколько поперечных сечений стержня и в каждом из них найти внутренние силы, то будет видно, что они изменяются в зависимости от расположения сечения. Расположение сечения определяется координатой z. То есть, усилия являются функциями z, и эти функции могут быть
представлены в виде графиков.
Графики функции , , , , , называются эпюрами внутренних сил.
При рассмотрении стержня на плоскостиOyzможет быть построено только три эпюры , , .
Для выполнения расчета на прочность необходимо знать наибольшее значение каждого из усилий и расположение сечений, в которых они этих значений достигают.
Сечения, в которых усилия достигают наибольших значений (по модулю),
принято считать «опасными».
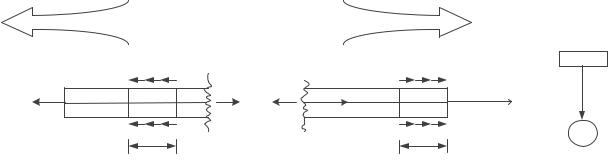
а) Усилие N(продольное усилие).
На рис. 23 показан рассеченный стержень, в сечении которого возникает положительное (растягивающее) усилие N.
Рис. 23 |
∑Z= 0, которое |
Неизвестное усилие N должно находиться из уравнения |
составляется для одной из частей стержня. Чтобы сила N и нагрузка уравновесили друг друга, они должны быть направлены в разные стороны.
Из рис. 23 видно, что внешние силы, вызывающие растягивающее усилие N,
направлены «от рассматриваемого сечения». То есть:
· (для левой части стержня),
